こんにちは、リンス(@Lins016)です。
今回は定義域の一端が変化する3次関数の最大最小について学習していこう。
3次関数の最大最小の場合分け
今回学習するのは、グラフが固定されていて定義域の一端が変化する関数の最大最小問題だ。定義域の一端が変化することによって、最大値や最小値をとる\(\small{ \ x \ }\)が変化していくことに注意しよう。まずは定義域内に極値を含むか含まないかっていうところから考えていこう。定義域内に極値を含まない場合は両端が最大最小になるけど、極値を含む場合は、極値と定義域の両端の値を比較して最大最小を求める必要があるからね。
\(\small{ \ y=x^3-3x \ }\)の区間\(\small{ \ -1 \leqq x \leqq a \ }\)における最大値と最小値
青い点の最大値と最小値が\(\small{ \ a \ }\)の位置によって変化する
①定義域の両端が最大最小
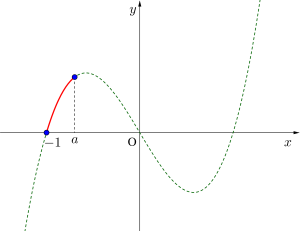
②定義域の左端と極大値が最大最小
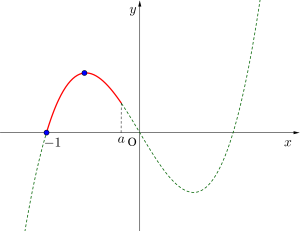
③定義域の右端と極大値が最大最小
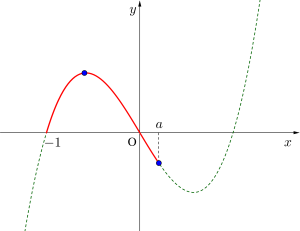
④極大値と極小値が最大最小
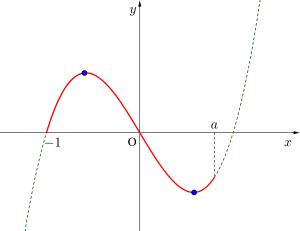
⑤極小値と定義域の右端が最大最小
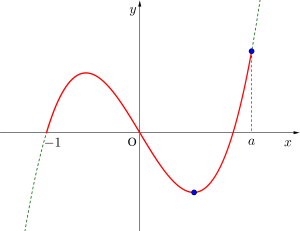
定義域の一端が変化する最大最小
定義域の一端が変化する最大最小問題は
- 固定されてる一端の\(\small{ \ y \ }\)座標と同じ\(\small{ \ y \ }\)座標になる\(\small{ \ x \ }\)座標を調べる。
- 極値と同じ\(\small{ \ y \ }\)座標の\(\small{ \ x \ }\)座標を調べる。
- 定義域内に極値を含む、含まないに場合分け
- 定義域内に極値を含む場合は、極値が最大(最小)になるか、定義域の一端が最大(最小)になるか1・2の値に注意して場合分け
これをグラフを書いて確認しながら場合分けしていこう。
求めるのは最大値と最小値だけど、実際は最大最小となるときの\(\small{ \ x \ }\)の値がどう変化しているのか注意しよう。
関数\(\small{ \ f(x)=x^3-9x^2+15x+5 \ }\)の\(\small{ \ 0 \leqq x \leqq a \ (a \gt 0) \ }\)における最大値と最小値を求めよ。ただし、\(\small{ \ a \ }\)は定数とする。
\(\small{ \ f(x)=x^3-9x^2+15x+5 \ }\)
\(\small{ \ \begin{eqnarray}f'(x)&=& 3x^2-18x+15\\
&=& 3(x-1)(x-5)\end{eqnarray} \ }\)
よって増減表は
\(\small{ \ \begin{array}{c|ccccc}
x & \cdots & 1 & \cdots & 5 & \cdots \\
\hline
f’(x) & + & 0 & - & 0 & + \\
\hline
f(x) & \nearrow & 12 & \searrow & -20 & \nearrow
\end{array} \ }\)
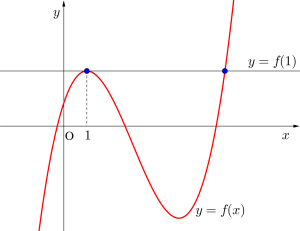
\(\small{ \ f(1)=12 \ }\)より\(\small{ \ f(x)=f(1) \ }\)とすると
\(\small{ \ x^3-9x^2+15x+5=12 \ }\)
\(\small{ \ x^3-9x^2+15x-7=0 \ }\)
\(\small{ \ (x-1)^2(x-7)=0 \ }\)
\(\small{ \ \therefore x=7 \ }\)
\(\small{ \ f(0)=5 \ }\)より\(\small{ \ f(x)=f(0) \ }\)とすると
\(\small{ \ x^3-9x^2+15x+5=5 \ }\)
\(\small{ \ x^3-9x^2+15x=0 \ }\)
\(\small{ \ x(x^2-9x+15)=0 \ }\)
\(\small{ \ \therefore x=\displaystyle \frac{9\pm\sqrt{21}}{2} \ }\)
(i)\(\small{ \ a \lt 1 \ }\)のとき
最小値\(\small{ \ 5 \ (x=0) \ }\)
最大値\(\small{ \ a^3-9a^2+15a+5 \ (x=a) \ }\)
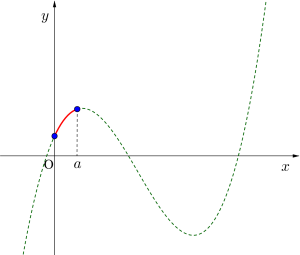
(ii)\(\small{ \ 1 \leqq a \lt \displaystyle \frac{9-\sqrt{21}}{2} \ }\)のとき
最小値\(\small{ \ 5 \ (x=0) \ }\)
最大値\(\small{ \ 12 \ (x=1) \ }\)
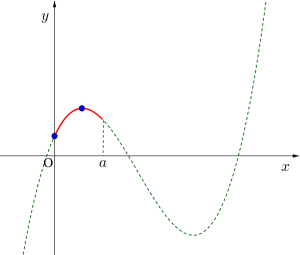
(iii)\(\small{ \ \displaystyle \frac{9-\sqrt{21}}{2} \leqq a \lt 5 \ }\)のとき
最小値\(\small{ \ a^3-9a^2+15a+5 \ (x=a) \ }\)
最大値\(\small{ \ 12 \ (x=1) \ }\)
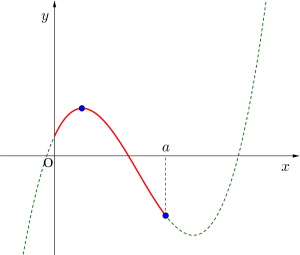
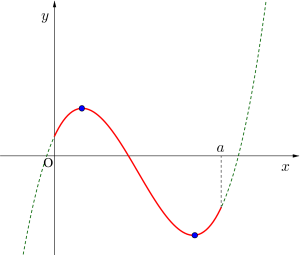
(iv)\(\small{ \ 5 \leqq a \lt 7 \ }\)のとき
最小値\(\small{ \ -20 \ (x=5) \ }\)
最大値\(\small{ \ 12 \ (x=1) \ }\)
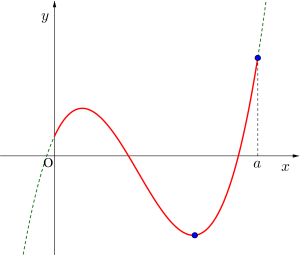
(v)\(\small{ \ a \geqq 7 \ }\)
最小値\(\small{ \ -20 \ (x=5) \ }\)
最大値\(\small{ \ a^3-9a^2+15a+5 \ (x=a) \ }\)

Point
①定義域に極値が含まれるか含まれないかで場合分け
②定義域の両端と極値と比較して場合分け

