こんにちは、リンス(@Lins016)です。
今回は三次関数の対称性と変曲点について学習していこう。
三次関数は変曲点に関して対称
三次関数は変曲点と呼ばれる点について対称なんだ。
で、その変曲点って何ってことになるんだけど、元の関数を2度微分した\(\small{ \ y'' \ }\)(二階微分)が\(\small{ \ y''=0 \ }\)で、かつその前後で\(\small{ \ y'' \ }\)の符号が変わる点のことなんだ。理系の人は数学Ⅲで学ぶけど、文系の人もどんな点なのかきちんと知っておこう。
変曲点とは?
グラフの凸が変化する点で図の青い部分は上に凸、図の赤い部分は下に凸になる。この凸の具合が変化するところを変曲点という。
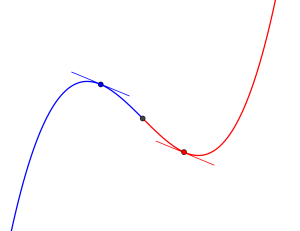
図を見てもわかるけど上に凸の部分の点における接線は曲線より上側にあって、下に凸の部分の点における接線は曲線より下側にあるんだ。ってことは変曲点における接線の方程式はちょうど曲線と交差するように交わる。
三次関数の対称性
三次関数は変曲点において点対称なグラフであるってことを覚えておこう。対称である証明も確認しておこう。
-

三次関数の点対称
3次関数のグラフは変曲点に関して対称なグラフであることについて解説しています。
続きを見る
三次関数のグラフと直線が交わるとき、直線が変曲点を通ることで3次関数のグラフと直線もまとめて点対称であるってことになるよね。今回は微分を学習しているけど、積分で面積求めたりする場合に簡単に求めることが出来るからね。
今回は三次関数についてだけ学習しているから\(\small{ \ y''=0 \ }\)の点が変曲点ってことで問題ないんだけど、三次関数以外の関数の場合、\(\small{ \ y''=0 \ }\)、かつその前後で\(\small{ \ y'' \ }\)の符号が変わるっていうのが変曲点を持つ条件になるから、三次関数以外の変曲点を利用する理系の人はしっかりと覚えておこう。
ちなみに三次関数\(\small{ \ y=ax^3+bx^2+cx+d \ }\)を2回微分すると\(\small{ \ y’’=6ax+2b \ }\)になるから、変曲点の\(\small{ \ x \ }\)座標は\(\small{ \ x=-\displaystyle \frac{b}{3a} \ }\)になる。
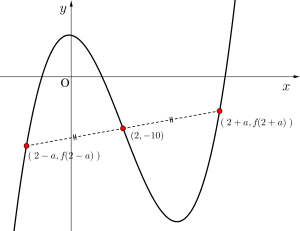
\(\small{ \ y=x^3-6x^2-x+8 \ }\)が点\(\small{ \ (2, \ -10) \ }\)に関して対称なグラフであることを証明せよ。
\(\small{ \ f(x)=x^3-6x^2-x+8 \ }\)とすると、\(\small{ \ y=f(x) \ }\)が点\(\small{ \ (2, \ -10) \ }\)に関して対称なグラフであるためには任意の\(\small{ \ a \ }\)で
\(\small{ \ f(2)=\displaystyle \frac{f(2-a)+f(2+a)}{2} \ }\)が成り立てばよい。
\(\small{ \ f(2-a)=-a^3+a-10 \ }\)
\(\small{ \ f(2+a)=a^3+a-10 \ }\)
\(\small{ \ \displaystyle \frac{f(2-a)+f(2+a)}{2}=-10 \ }\)
よって\(\small{ \ y=x^3-6x^2-x+8 \ }\)が点\(\small{ \ (2, \ -10) \ }\)に関して対称なグラフである。

Point 三次関数の対称性と変曲点
①三次関数のグラフは変曲点について対称
②三次関数の変曲点とは\(\small{ \ y’’=0 \ }\)を満たす点


