こんにちは、リンス(@Lins016)です。
今回はベン図の書き方について学習していこう。
ベン図とは
ベン図とはイギリスの数学者によって考案された図で、集合の問題を考えるときに非常に有効な図なんだ。
ベン図をうまく利用する方法を学習していくからきちんとマスターしてほしい。


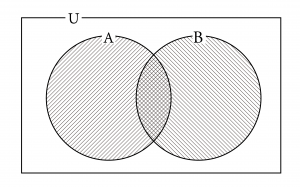
ベン図の書き方
ベン図を利用する場合、全体集合\(\small{ \ \mathrm{U} \ }\)を長方形で書いて、部分集合を円で書くようにしよう。
よく見かけるからベン図を書いたことある人ならそうしてるよね。
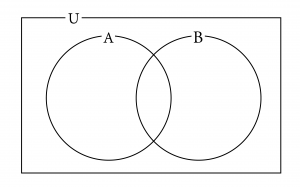
次に求めたい集合が\(\small{ \ \mathrm{A\cap B} \ }\)のようになっていたら、左側に書いてある集合(この場合は\(\small{ \ \mathrm{A} \ }\))を斜線で塗ろう。
次に右側に書いてる集合(この場合は\(\small{ \ \mathrm{B} \ }\))をさっきの斜線とは傾きを変えて塗ろう。

ベン図を利用する場合、ここまでしておこう。
A∩B(AかつB)
次に\(\small{ \ \mathrm{A\cap B} \ }\)について考えてみよう。
\(\small{ \ \mathrm{A\cap B} \ }\)は「\(\small{ \ \mathrm{A} \ }\)かつ\(\small{ \ \mathrm{B} \ }\)」だから\(\small{ \ \mathrm{A} \ }\)にも\(\small{ \ \mathrm{B} \ }\)属している部分になるよね。
これは斜線が二つ重なっている部分で共通部分や積集合って呼ぶからね。

A∪B(AまたはB)
次に\(\small{ \ \mathrm{A\cup B} \ }\)について考えてみよう。
\(\small{ \ \mathrm{A\cup B} \ }\)は「\(\small{ \ \mathrm{A} \ }\)または\(\small{ \ \mathrm{B} \ }\)」だから\(\small{ \ \mathrm{A} \ }\)か\(\small{ \ \mathrm{B} \ }\)のどちらかに属している部分になるよね。
これは斜線が塗られている部分ならどこでもいいってことだから、斜線が二つ重なっている部分と斜線が一つの部分で和集合って呼ぶからね。

全体集合\(\small{ \ \mathrm{U} \ }\)、部分集合\(\small{ \ \mathrm{A} \ }\)、部分集合\(\small{ \ \mathrm{B} \ }\)のとき次のベン図を図示せよ。
(1)\(\small{ \ \mathrm{\overline{ A }\cap B} \ }\)
(2)\(\small{ \ \mathrm{\overline{ A }\cap \overline{B}} \ }\)

(1)\(\small{ \ \mathrm{\overline{ A }\cap B} \ }\)
部分集合をそれぞれ斜線で塗ると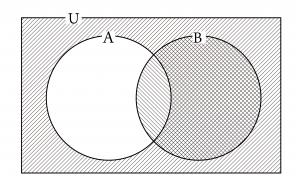
求める集合は共通部分より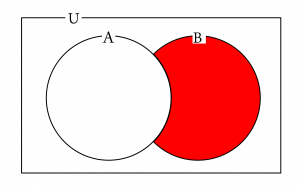
(2)\(\small{ \ \mathrm{\overline{ A }\cap \overline{B}} \ }\)
部分集合をそれぞれ斜線で塗ると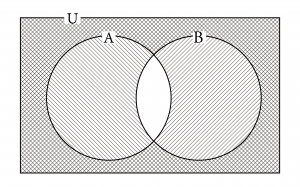
求める集合は共通部分より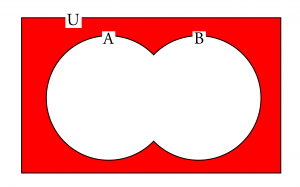

\(\small{ \ \mathrm{\overline{ A }\cap \overline{B}=\overline{A\cup B} } \ }\)
\(\small{ \ \mathrm{\overline{ A }\cup \overline{B}=\overline{A\cap B} } \ }\)
三つ以上部分集合があるベン図
三つ以上の部分集合があるベン図は、二つの場合と同じで斜線の角度を変えてそれぞれの部分集合を塗っていこう。
ただ、四つ以上の部分集合のベン図を書くのは難しいし、ほとんど出題されることないから、三つの部分集合までを確実に書けるようにマスターしておこう。
Point ベン図の書き方
①部分集合を斜線で塗る
②「かつ」「または」を塗りで判別する
③ド・モルガンの法則を利用する

