こんにちは、リンス(@Lins016)です。
今回は円の方程式の決定について学習していこう。
円の方程式の求め方
円の方程式は中心と半径で表される平方形と、平方形を展開した一般形の二通りの表し方がある。
だから問題によって使い分けていくことが重要なんだ。円の方程式を決定する問題では、平方形だと\(\small{ \ a、b、r \ }\)の三文字を、一般形だと\(\small{ \ l、m、n \ }\)の三文字を求めなければいけないよね。
だけど、どっちの形も同じ三文字を求めるからといって、どっちの形を使ってもいいってことにはならないんだ。
それぞれいつ使うのか、パターンをしっかりと理解してなるべく少ない計算量で問題を解こう。
・平方形
\(\small{(x-a)^2+(y-b)^2=r^2}\)
・一般形
\(\small{x^2+y^2+lx+my+n=0}\)
平方形の利用
円の方程式の決定問題で、問題文に中心と半径に関することが書いてある時は平方形を利用しよう。
というより、この後に記述する一般形を使う場合は、与えられた三点を通るときに利用するから、むしろそれ以外の問題は、全て平方形を利用して円の方程式を決定すると思っていて問題ない。
一般形の利用
円の方程式の決定問題では、与えられた\(\small{ \ 3 \ }\)点を通るときは一般形を利用しよう。
\(\small{ \ 3 \ }\)点が与えられたときに、平方形を利用すると計算量がとんでもないことになるからね。円の方程式を求めた後、次に問題が続く場合は、求めた円の方程式を平方形にして中心と半径も確認しよう。
次の円の方程式を求めよ。
(1)\(\small{2}\)点\(\small{ \ (0,1)、(4,-1) \ }\)を通り、直線\(\small{ \ y=x-1 \ }\)上に中心がある円
(2)点\(\small{ \ (-2,1) \ }\)を通り、\(\small{ \ x \ }\)軸、\(\small{ \ y \ }\)軸に接する円
(3)\(\small{ \ 3 \ }\)点\(\small{ \ (0,1)、(3,2)、(6,-7) \ }\)を通る円
(1)中心の座標を\(\small{ \ (t,t-1) \ }\)とすると円の方程式は\(\small{ \ (x-t)^2+(y-t+1)^2=r^2 \ }\)とおける。
\(\small{ \ 2 \ }\)点\(\small{ \ (0,1)、(4,-1) \ }\)を通るので、それぞれ代入すると、
\(\small{(-t)^2+(1-t+1)^2=r^2}\)
\(\small{(4-t)^2+(-1-t+1)^2=r^2}\)
これから\(\small{ \ r \ }\)を消去すると、
\(\small{2t^2-4t+4=2t^2-8t+16}\)
\(\small{4t-12=0}\)
\(\small{t=3}\)、\(\small{r^2=10}\)
よって求める円の方程式は
\(\small{(x-3)^2+(y-2)^2=10}\)

(2)点第\(\small{ \ 2 \ }\)象限の点\(\small{ \ (-2,1) \ }\)を通ることと、\(\small{ \ x \ }\)軸、\(\small{ \ y \ }\)軸に接するに接することから求める円の方程式は\(\small{ \ (x+r)^2+(y-r)^2=r^2 \ }\)とおける。ただし、\(\small{ \ r\gt 0}\)
点\(\small{ \ (-2,1) \ }\)を円の方程式に代入して、
\(\small{(-2+r)^2+(1-r)^2=r^2}\)
\(\small{r^2-6r+5=0}\)
\(\small{(r-1)(r-5)}=0\)
\(\small{r=1、5}\)
よって求める円の方程式は
\(\small{(x+1)^2+(y-1)^2=1}\)、
\(\small{(x+5)^2+(y-5)^2=25}\)

(3)円の方程式を\(\small{ \ x^2+y^2+lx+my+n=0 \ }\)とおく。
\(\small{ \ (0,1)、(3,2)、(6,-7) \ }\)をそれぞれ代入し、
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
m+n+1=0 \\
3l+2m+n+13=0\\
6l-7m+n+85=0
\end{array}
\right.
\end{eqnarray}}\)
これを解いて
\(\small{l=-6、m=6、n=-7}\)
よって求める方程式は、
\(\small{x^2+y^2-6x+6y-7=0}\)


そしたら平方形だけでいいじゃんと思うかもしれないけど、\(\small{ \ 3 \ }\)点を通るときに平方形に代入すると計算が大変すぎて死んじゃうよね。
だから一般形があると思ってていい笑。平方形と一般形をうまく使い分けて、すべての問題を素早く解けるようにしていこう。
Point 円の方程式の決定
①3点を通る円を求める場合は一般形を利用しよう
②3点を通る円以外は平方形を利用しよう
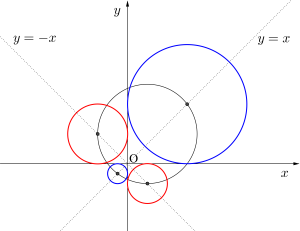
円\(\small{ \ (x-2)^2+(y-3)^2=25 \ }\)上に中心を持ち、\(\small{ \ x \ }\)軸、\(\small{ \ y \ }\)軸のいずれにも接する円の方程式をすべて求めよ。
\(\small{ \ x \ }\)軸、\(\small{ \ y \ }\)軸のいずれにも接する円の方程式は
\(\small{ \ (x-t)^2+(y-t)^2=t^2 \ }\)または、\(\small{ \ (x-t)^2+(y+t)^2=t^2 \ }\)とおける。
(i)中心の座標が\(\small{ \ (t、t) \ }\)の場合
\(\small{ \ (x-2)^2+(y-3)^2=25 \ }\)上に中心があるので\(\small{ \ (t、t) \ }\)を代入すると
\(\small{ \ (t-2)^2+(t-3)^2=25 \ }\)
\(\small{ \ 2t^2-10t-12=0 \ }\)
\(\small{ \ t^2-5t-6=0 \ }\)
\(\small{ \ (t-6)(t+1)=0 \ }\)
\(\small{ \ \therefore t=6、-1 \ }\)
よって求める円の方程式は
\(\small{ \ (x-6)^2+(y-6)^2=36 \ }\)
\(\small{ \ (x+1)^2+(y+1)^2=1 \ }\)
(ii)中心の座標が\(\small{ \ (t、-t) \ }\)の場合
\(\small{ \ (x-2)^2+(y-3)^2=25 \ }\)上に中心があるので\(\small{ \ (t、-t) \ }\)を代入すると
\(\small{ \ (t-2)^2+(-t-3)^2=25 \ }\)
\(\small{ \ 2t^2+2t-12=0 \ }\)
\(\small{ \ t^2+t-6=0 \ }\)
\(\small{ \ (t+3)(t-2)=0 \ }\)
\(\small{ \ \therefore t=2、-3 \ }\)
よって求める円の方程式は
\(\small{ \ (x-2)^2+(y+2)^2=4 \ }\)
\(\small{ \ (x+3)^2+(y-3)^2=9 \ }\)
(i)(ii)より
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
(x-6)^2+(y-6)^2=36 \\
(x+1)^2+(y+1)^2=1 \\
(x-2)^2+(y+2)^2=4 \\
(x+3)^2+(y-3)^2=9 \\
\end{array}
\right.
\end{eqnarray} \ }\)