こんにちは、リンス(@Lins016)です。
今回は円が切り取る線分(弦)の長さについて学習していこう。
円が切り取る線分(弦)の長さ
円と直線が二つの点で交わるとき、その二点を結ぶ線分の長さを求めてみよう。
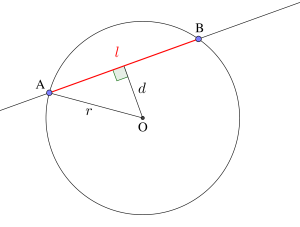
①点と直線の距離の利用
\(\small{ \ l=2\sqrt{r^2-d^2} \ }\)
②解の公式または解と係数の関係の利用
点と直線の距離の公式を利用して円が切り取る線分の長さを求める
図のように「線分の中点」と「円の中心」と「円と直線の共有点」で直角三角形ができるからこの三角形を利用して円が切り取る線分の長さを求めよう。

まずは円の中心から直線までの距離を点と直線の距離の公式を使って求めよう。
このとき\(\small{ \ y=mx+n \ }\)の形の直線を\(\small{ \ ax+by+c=0 \ }\)の形に変形すると思うけど、点と直線の距離の公式を利用するときは、\(\small{ \ a, \ b, \ c \ }\)ともに整数になるようにしておこう。
例えば\(\small{ \ y=\displaystyle \frac{1}{2}x+\displaystyle \frac{1}{3} \ }\)だと\(\small{ \ 3x-6y+2=0 \ }\)にするってこと。
そうすることで点と直線の距離の公式を使うときに分数に分数が重なることがなくなるから計算が楽になるからね。
円の中心と直線の距離を求めたら、その求めた距離と円の半径を利用して三平方の定理を使おう。
これで弦の半分の長さが求まるから、あとは二倍すればいいよね。
-

点と直線の距離
点と直線の距離の公式について証明します。座標を利用する方法で解説しています。
続きを見る
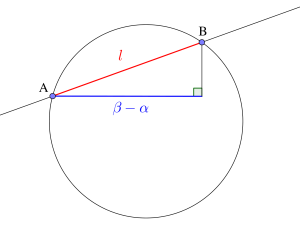
共有点の座標・解と係数の関係から円が切り取る線分の長さを求める
今度は円と直線の共有点から二点間の距離を求めてみよう。
まずは直線の方程式を\(\small{ \ y=mx+n \ }\)の形にして、円の方程式に代入しよう。
すると\(\small{ \ x \ }\)の二次方程式ができる。
(もちろん直線の方程式によっては\(\small{ \ x=py+q \ }\)の形にして\(\small{ \ y \ }\)の二次方程式でも構わない。)
この二次方程式の解が円と直線の共有点の\(\small{ \ x \ }\)座標になるから、\(\small{ \ x \ }\)座標を求めて、これを直線の方程式に代入して\(\small{ \ y \ }\)座標を求めると共有点の座標が求まる。
二点の座標が求まったら、三平方の定理を利用して二点間の距離を出せばいいよね。
ただ円と直線の共有点の\(\small{ \ x \ }\)座標が複雑な値だと計算が大変になる。
だから円と直線の方程式を連立した二次方程式が解の公式を使わないと解けないような場合は直接計算せずに解と係数の関係を利用しよう。
直線の方程式を円の方程式に代入した二次方程式の解を\(\small{ \ x=\alpha, \ \beta \ }\)とすると
まずは共有点の\(\small{ \ x \ }\)座標の差\(\small{ \ \beta-\alpha \ }\)を求めよう。
これは解と係数の関係を利用して
\(\small{ \ (\beta-\alpha)^2=(\alpha+\beta)^2-4\alpha\beta \ }\)
を計算することで求めることができる。
あとは直線の方程式が\(\small{ \ y=mx+n \ }\)だとすると傾き\(\small{ \ m \ }\)を利用して
\(\small{ \ \sqrt{m^2+1}(\beta- \alpha) \ }\)を求めればいい。
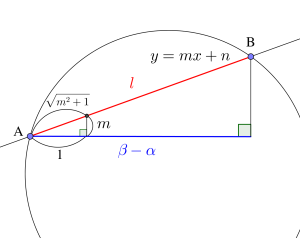
この方法だとあまり複雑な計算がないから、共有点の座標が複雑な値の場合でも割と簡単に求めることができる。
-

解と係数の関係の証明
二次方程式と三次方程式の解と係数の関係の証明について詳しく解説しています。
続きを見る
直線\(\small{ \ 2x-y-2=0 \ }\)が円\(\small{ \ x^2+y^2-2x-2y=0 \ }\)によって切り取られる弦の長さと弦の中点の座標を求めよ。
・点と直線の距離を利用する場合
\(\small{ \ x^2+y^2-2x-2y=0 \ }\)を変形すると
\(\small{ \ (x-1)^2+(y-1)^2=2 \ }\)
円の中心\(\small{ \ (1, \ 1) \ }\)と直線\(\small{ \ 2x-y-2=0 \ }\)の距離を\(\small{ \ d \ }\)とすると
\(\small{ \ d=\displaystyle \frac{|2-1-2}{2^2+(-1)^2}=\displaystyle \frac{\sqrt{5}}{5} \ }\)
求める弦の長さを\(\small{ \ l \ }\)とすると、三平方の定理より円の半径と\(\small{ \ d \ }\)を使って
\(\small{ \ \displaystyle \frac{l}{2}=\sqrt{2-\displaystyle \frac{1}{5}}=\displaystyle \frac{3\sqrt{5}}{5} \ }\)
よって求める弦の長さは\(\small{ \ l=\displaystyle \frac{6\sqrt{5}}{5} \ }\)
\(\small{ \ x^2+y^2-2x-2y=0 \ }\)に\(\small{ \ y=2x-2 \ }\)を代入すると
\(\small{ \ 5x^2-14x+8=0 \ }\)
この二次方程式の解を\(\small{ \ x=\alpha, \ \beta \ }\)とすると
解と係数の関係より
\(\small{ \ \alpha+\beta=\displaystyle \frac{14}{5} \ }\)
求める中点の\(\small{ \ x \ }\)座標は\(\small{ \ \displaystyle \frac{\alpha+\beta}{2} \ }\)になるから
\(\small{ \ x=\displaystyle \frac{7}{5} \ }\)
\(\small{ \ y=2x-2 \ }\)に代入して\(\small{ \ y=\displaystyle \frac{4}{5} \ }\)
よって求める座標は\(\small{ \ \left(\displaystyle \frac{7}{5}, \ \displaystyle \frac{4}{5}\right) \ }\)
・共有点を直接求めて計算する場合
\(\small{ \ 2x-y-2=0 \ }\)を\(\small{ \ y=2x-2 \ }\)変形して
\(\small{ \ x^2+y^2-2x-2y=0 \ }\)に代入すると
\(\small{ \ 5x^2-14x+8=0 \ }\)
\(\small{ \ (5x-4)(x-2)=0 \ }\)
よって\(\small{ \ x=2, \ \displaystyle \frac{4}{5} \ }\)
\(\small{ \ y=2x-2 \ }\)に代入して
\(\small{ \ y=2, \ -\displaystyle \frac{2}{5} \ }\)
よって共有点の座標は
\(\small{ \ \left(2, \ 2\right), \ \ \left(\displaystyle \frac{4}{5}, \ -\displaystyle \frac{2}{5}\right) \ }\)
よって弦の長さを\(\small{ \ l \ }\)とすると
\(\small{ \ l=\sqrt{\left(2-\displaystyle \frac{4}{5}\right)^2+\left(2+\displaystyle \frac{2}{5}\right)^2}\\
=\displaystyle \frac{6\sqrt{5}}{5} \ }\)
中点の座標は\(\small{ \ \left(\displaystyle \frac{2+\displaystyle \frac{4}{5}}{2}, \ \displaystyle \frac{2-\displaystyle \frac{2}{5}}{2}\right)\\
=\left(\displaystyle \frac{7}{5}, \ \displaystyle \frac{4}{5}\right) \ }\)
・解と係数の関係を利用する場合
\(\small{ \ 2x-y-2=0 \ }\)を\(\small{ \ y=2x-2 \ }\)変形して
\(\small{ \ x^2+y^2-2x-2y=0 \ }\)に代入すると
\(\small{ \ 5x^2-14x+8=0 \ }\)
この二次方程式の解を\(\small{ \ x=\alpha, \ \beta \ (\alpha \lt \beta ) \ }\)とすると
解と係数の関係より
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
\alpha+\beta=\displaystyle \frac{14}{5}\\
\alpha\beta=\displaystyle \frac{8}{5}
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{\begin{eqnarray} \ (\beta-\alpha)^2&=&(\alpha+\beta)^2-4\alpha\beta \\
&=&\left(\displaystyle \frac{14}{5}\right)^2-4\cdot\displaystyle \frac{8}{5}\\
&=&\displaystyle \frac{36}{25}\ \end{eqnarray}}\)
よって\(\small{ \ \beta-\alpha=\displaystyle \frac{6}{5} \ }\)
求める弦の長さは\(\small{ \ \sqrt{2^2+1}(\beta-\alpha) \ }\)より
\(\small{ \ \displaystyle \frac{6\sqrt{5}}{5} \ }\)
求める中点の\(\small{ \ x \ }\)座標は\(\small{ \ \displaystyle \frac{\alpha+\beta}{2} \ }\)になるから
\(\small{ \ x=\displaystyle \frac{7}{5} \ }\)
\(\small{ \ y=2x-2 \ }\)に代入して\(\small{ \ y=\displaystyle \frac{4}{5} \ }\)
よって求める座標は\(\small{ \ \left(\displaystyle \frac{7}{5}, \ \displaystyle \frac{4}{5}\right) \ }\)

弦の長さは点と直線の距離を利用すれば、円と直線の方程式を連立した二次方程式は必要ない。
だけど中点や共有点を求める場合は二次方程式が必要になるってことを覚えておこう。
弦の長さだけなら点と直線の距離の利用でいいけど、中点まで必要なら結局二次方程式を立てる必要があるから初めから共有点を求める二次方程式を作って共有点を求めるか解と係数の関係を使った方がいい。
Point 円が切り取る線分(弦)の長さ
①弦の長さは点と直線の距離を利用しよう
②弦の中点の座標が必要な場合は二次方程式を立てて解と係数の関係から求めよう
-

放物線が切り取る線分の長さ
放物線が切り取る線分の長さについて学習します。放物線がx軸やy=mx+nの直線を切り取る線分の長さの求め方について解説しています。
続きを見る
座標平面上に中心が\(\small{ \ (2, \ 2) \ }\)で半径が\(\small{ \ 1 \ }\)の円\(\small{ \ C \ }\)と、原点を通り傾きが\(\small{ \ m \ }\)の直線\(\small{ \ l \ }\)がある,
(1)円\(\small{ \ C \ }\)と直線\(\small{ \ l \ }\)が異なる\(\small{ \ 2 \ }\)点で交わるための\(\small{ \ m \ }\)の値の範囲を求めよ。
(2)円\(\small{ \ C \ }\)と直線\(\small{ \ l \ }\)の\(\small{ \ 2 \ }\)つのの共有点と円\(\small{ \ C \ }\)の中心とでできる三角形の面積が最大となるような\(\small{ \ m \ }\)の値を求めよ。
(1)円の中心と直線の距離が半径より短ければいい。
\(\small{ \ \displaystyle \frac{|2m-2|}{\sqrt{m^2+1}}\lt 1 \ }\)
\(\small{ \ |2m-2| \lt \sqrt{m^2+1} \ }\)
\(\small{ \ 4m^2-8m+4\lt m^2+1 \ }\)
\(\small{ \ 3m^2-8m+3 \lt 0 \ }\)
\(\small{ \ \therefore\displaystyle \frac{4-\sqrt{7}}{3}\lt m \lt \displaystyle \frac{4+\sqrt{7}}{3} \ }\)
(2)円\(\small{ \ C \ }\)と直線\(\small{ \ l \ }\)の交点を\(\small{ \ \mathrm{P, \ Q} \ }\)円の中心を\(\small{ \ \mathrm{O} \ }\)、\(\small{ \ \triangle \mathrm{POQ}=\theta \ }\)とすると
三角形の面積\(\small{ \ \mathrm{S} \ }\)は
\(\small{ \ \mathrm{S}=\displaystyle \frac{1}{2}\mathrm{OP}\cdot\mathrm{OQ}\sin\theta \ }\)
\(\small{ \ \mathrm{OP}=\mathrm{OQ}=1 \ }\)より
\(\small{ \ \sin\theta=1 \ }\)のとき面積は最大になる。
このとき円\(\small{ \ C \ }\)の中心\(\small{ \ \mathrm{O} \ }\)と直線\(\small{ \ l \ }\)の距離は\(\small{ \ \displaystyle \frac{1}{\sqrt{2}} \ }\)になる
\(\small{ \ \displaystyle \frac{|2m-2|}{\sqrt{m^2+1}}=\displaystyle \frac{1}{\sqrt{2}}\ }\)
\(\small{ \ \sqrt{2}|2m-2|=\sqrt{m^2+1} \ }\)
\(\small{ \ 8m^2-16m+8=m^2+1 \ }\)
\(\small{ \ 7m^2-16m+7=0 \ }\)
\(\small{ \ \therefore m=\displaystyle \frac{8\pm\sqrt{15}}{7} \ }\)


