こんにちは、リンス(@Lins016)です。
今回は円周外の点から引いた円の接線の方程式について学習していこう。
接線の公式・判別式・点と直線の距離の利用
円周外の点から円に接線を引くと接線は\(\small{ \ 2 \ }\)本引くことができるよね。まずこれを頭に入れておこう。
といっても、\(\small{ \ 2 \ }\)本の直線の方程式を別々に求める必要はなくて、円に接する式を\(\small{ \ 1 \ }\)つ立てて接線を求めたら、答えが\(\small{ \ 2 \ }\)つ出るから、\(\small{ \ 2 \ }\)本の接線になるんだ。
(1)接線の公式を利用する方法
(2)判別式を利用する方法
(3)点と直線の距離を利用する方法
円周外の点から引いた接線の求め方は\(\small{ \ 3 \ }\)パターンある。それぞれ一長一短あるから、問題によって解き方を使い分けよう。
接線の方程式と接点
円周上の接点が求まると接線も求まるから、接点を求めてしまえば接線も求まるよね。でも接点が求まらなくても接線を求めることもできるんだ。
接点を求めるなら接線の公式を利用する方法になるし、まずは接線から求めたいなら判別式を利用する方法か点と直線の距離を利用する方法になる。
問題によって解法をうまく使い分けて計算量をなるべく少なくしよう。
円の接線の方程式の公式
円の接点が分かっているときは円の接線の公式を利用しよう。
-

接点が与えられた円の接線の方程式
接点が与えられた問題の注意点について詳しく解説しています。
続きを見る
接点の座標を求める問題の方が圧倒的に多いけど、確実におさえておこう。
判別式を利用した円の接線の求め方
円周外の点から円に接線を引く場合、判別式が利用できる。
まずは円の方程式\(\small{ \ (x-a)^2+(y-b)^2=r^2 \ }\)に直線の方程式\(\small{ \ y=mx+n \ }\)を代入して、\(\small{ \ x \ }\)の二次方程式を作るんだ。
この二次方程式が\(\small{ \ 2 \ }\)つの解を持つなら円と直線は2点で交わるし、\(\small{ \ 1 \ }\)つの解(重解)を持つなら円と直線は接するし、解を持たないなら円と直線は交わらないよね。だからこの二次方程式が重解を持つなら円と直線は接するって言えるよね。
ただ注意しないといけないこともある。例えば、円周外の点\(\small{ \ (2, \ 3) \ }\)から引いた接線を求める場合、接線の方程式を\(\small{ \ y=m(x-2)+3 \ }\)っておくと思うんだけど、この形だとどんな\(\small{ \ m \ }\)の値をとっても\(\small{ \ y \ }\)軸に平行な直線にはならないんだ。
円周外から引いた接線は必ず\(\small{ \ 2 \ }\)本引けるから、判別式を使って\(\small{ \ m \ }\)の値が\(\small{ \ 1 \ }\)つしか出なかったら、もう\(\small{ \ 1 \ }\)つの接線は\(\small{ \ y \ }\)軸に平行な直線になるから\(\small{ \ x=2 \ }\)が接線になるから覚えておこう。(\(\small{ \ (2, \ 3) \ }\)を通る直線だからね。)
円の中心と直線の距離と円の半径
判別式で接線の方程式を求めればいいんだけど、判別式だと計算量がかなり多くなる問題もあるんだ。
だから計算量を抑えるためにもう\(\small{ \ 1 \ }\)つ接線の方程式の求め方を覚えておこう。それは点と直線の公式を利用する方法なんだ。
-

点と直線の距離
点と直線の距離の公式について証明します。座標を利用する方法で解説しています。
続きを見る
円の中心と直線の距離が半径と等しいとき、円と直線は接するって言えるよね。これを利用して接線の方程式を求めよう。
もちろんこれを利用して、円と直線が共有点を持つ、持たないも考えられるからね。
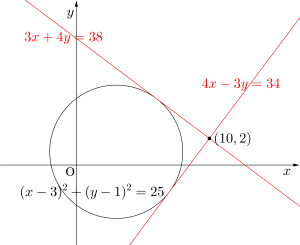
点\(\small{ \ \left(10, \ 2\right) \ }\)から\(\small{ \ \left(x-3\right)^2+\left(y-1\right)^2=25 \ }\)に引いた接線の方程式を求めよ。
円周上の点を\(\small{ \ \left(x_1,y_1\right) \ }\)とおくと
接線の方程式は
となる。
これが\(\small{ \ \left(10, \ 2\right) \ }\)を通るから
\(\small{ \ 7\left(x_1-3\right)+y_1-1=25 \ }\)
\(\small{ \ 7x_1+y_1=47\cdots② \ }\)
また\(\small{ \ \left(x_1, \ y_1\right) \ }\)は円周上の点より
\(\small{ \ \left(x_1-3\right)^2+\left(y_1-1\right)^2=25\cdots③ \ }\)
これを\(\small{ \ ② \ }\)を変形して\(\small{ \ ③ \ }\)に代入すると
\(\small{ \ \left(x_1-3\right)^2+\left(46-7x_1\right)^2=25 \ }\)
これを整理して
\(\small{ \ 50{x_1}^2-65x_1+2100=0 \ }\)
\(\small{ \ {x_1}^2-13x_1+42=0 \ }\)
\(\small{ \ \left(x_1-7\right) \left(x_1-6\right)=0 \ }\)
\(\small{ \ x_1=7, \ 6}\)
②に代入して
\(\small{\left(x_1, \ y_1\right)=\left(7, \ -2\right), \ \left(6, \ 5\right)}\)
よって求める方程式は①に代入して
\(\small{ \ 4x-3y=34 \ }\)、\(\small{ \ 3x+4y=38 \ }\)
(2)判別式を利用する
求める接線は\(\small{y}\)軸に平行な直線ではないから
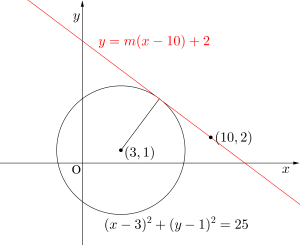
\(\small{ \ \left(10, \ 2\right) \ }\)を通るので\(\small{ \ y=m\left(x-10\right)+2 \ }\)とおける。
これを円の方程式に代入すると
整理して
判別式を求めると
\(\small{\begin{eqnarray}
\displaystyle \frac{D}{4}&=&(10m^2-m+3)^2-(m^2+1)(100m^2-20m-15)\\
&=&-24m^2+14m+24\\
&=&-2(4m+3)(3m-4)
\end{eqnarray}}\)
円と直線が接するので判別式\(\small{ \ =0 \ }\)となればよい。
\(\small{ \ m=\displaystyle \frac{4}{3}, \ -\displaystyle \frac{3}{4} \ }\)
よって求める接線の方程式は
\(\small{ \ y=\displaystyle \frac{4}{3}x-\displaystyle \frac{34}{3} \ }\)、\(\small{ \ y=-\displaystyle \frac{3}{4}x-\displaystyle \frac{38}{4}}\)
(3)点と直線の距離を利用する
求める接線は\(\small{y}\)軸に平行な直線ではないから
\(\small{\left(10, \ 2\right)}\)を通るので\(\small{ \ y=m\left(x-10\right)+2 \ }\)とおける。
円の中心とこの直線との距離が半径と同じになれば円と直線は接するから
\(\small{\displaystyle \frac{|3m-1-10m+2|}{\sqrt{m^2+1}}=5}\)
\(\small{|-7m+1|=5\sqrt{m^2+1}}\)
両辺を二乗して
\(\small{(-7m+1)=25(m^2+1)}\)
\(\small{12m^2-7m-12=0}\)
\(\small{(4m+3)(3m-4)=0}\)
\(\small{m=\displaystyle \frac{4}{3}, \ -\displaystyle \frac{3}{4}}\)
よって求める接線の方程式は
\(\small{y=\displaystyle \frac{4}{3}x-\displaystyle \frac{34}{3} \ }\)、\(\small{ \ y=-\displaystyle \frac{3}{4}x-\displaystyle \frac{38}{4}}\)

でも円の中心が原点にある場合は(解答\(\small{ \ 1 \ }\))のように接線の方程式を利用したらすごく簡単に答えを出すことができる。
接点の座標を求めるとしたら(解答\(\small{ \ 2 \ }\))の方が(解答\(\small{ \ 3 \ }\))よりいいかもしれないけど、それなら(解答\(\small{ \ 1 \ }\))の方が計算量が少くていいかな。
ってことは(解答2)はいらないじゃんって思うよね?
うん、確かになくてもいいかもしれない。だけど入試問題では問題文の誘導に従って解かないとといけない問題があるから、すべての解法を知っておく必要があるんだ。
Point 円周外の点から引いた円の接線の方程式
円周上にない点から引く接線の方程式は
①円の中心が原点なら接線の公式を利用
②中心が原点以外なら点と直線の距離の公式を利用
円\(\small{ \ C \ }\):\(\small{ \ x^2+y^2=5 \ }\)と点\(\small{ \ \mathrm{P}(3, \ 1) \ }\)がある。以下の問いに答えよ。
(1)円\(\small{ \ C \ }\)に点\(\small{ \ \mathrm{P}(3, \ 1) \ }\)から引いた接線の方程式を求めよ。また、接点と点\(\small{ \ \mathrm{P}(3, \ 1) \ }\)との長さも求めよ。
(2)\(\small{ \ \mathrm{P} \ }\)を通る直線\(\small{ \ y=m(x-3)+1 \ }\)が円\(\small{ \ C \ }\)と\(\small{ \ 2 \ }\)点\(\small{ \ \mathrm{M} \ }\)、\(\small{ \ \mathrm{N} \ }\)で交わるとき\(\small{ \ \mathrm{PM}\cdot \mathrm{PN} \ }\)の値を求めよ。
(3)(1)で求めた\(\small{ \ 2 \ }\)つの接線と円の交点(つまり接点)を通る直線の方程式は\(\small{ \ 3x+y=5 \ }\)であることを示せ。
(1)接点の座標を\(\small{ \ (a, \ b) \ }\)とすると、接線の方程式は\(\small{ \ ax+by=5 \ }\)
これが点\(\small{ \ \mathrm{P} \ }\)を通るので
\(\small{ \ 3a+b=5\cdots① \ }\)
また\(\small{ \ (a,b) \ }\)は円周上の点より
\(\small{ \ a^2+b^2=5\cdots② \ }\)
\(\small{①②}\)を連立して解くと\(\small{ \ (a,b)=(1, \ 2)、(2, \ -1) \ }\)
よって求める接線の方程式は
\(\small{ \ x+2y=5、2x-y=5 \ }\)
また接点と\(\small{ \ \mathrm{P} \ }\)との距離は
\(\small{ \ \sqrt{(3-1)^2+(1-2)^2}=\sqrt{5} \ }\)
(2)接点を\(\small{ \ \mathrm{T} \ }\)とすると方べきの定理より
\(\small{ \ \mathrm{PM}\cdot\mathrm{PN}=\mathrm{PT}^2 \ }\)が成り立つ。
よって\(\small{ \ \mathrm{PM}\cdot\mathrm{PN}=\mathrm{PT}^2=5 \ }\)
(3)接点の座標は\(\small{ \ (1, \ 2)、(2, \ -1) \ }\)より
これを通る直線は\(\small{ \ 3x+y=5 \ }\)である。
補足
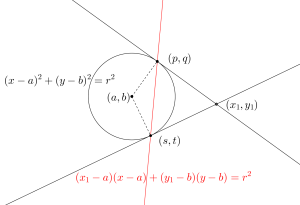
\(\small{(x-a)^2+(y-b)^2=r^2}\)上の
\(\small{ \ 2 \ }\)点\(\small{ \ (p, \ q)、(s, \ t) \ }\)における接線の方程式は
\(\small{(p-a)(x-a)+(q-b)(y-b)=r^2}\)と\(\small{(s-a)(x-a)+(t-b)(y-b)=r^2}\)になる
これが\(\small{ \ (x_1, \ y_1) \ }\)を通るから
\(\small{(p-a)(x_1-a)+(q-b)(y_1-b)=r^2}\)
\(\small{(s-a)(x_1-a)+(t-b)(y_1-b)=r^2}\)
これは
\(\small{(x_1-a)(x-a)+(y_1-b)(y-b)=r^2}\)を
\(\small{ \ (p, \ q)、(s, \ t) \ }\)が通る式にほかならない。
よって接点を結ぶ直線の方程式は
\(\small{(x_1-a)(x-a)+(y_1-b)(y-b)=r^2}\)となる。
-

方べきの定理の証明
相似を利用した三つのパターンについて解説しています。
続きを見る


