こんにちは、リンス(@Lins016)です。
今回は円順列について学習していこう。
円順列
順列っていくつかのものを一列に並べることだったけど、これを一列じゃなくて円形に並べる並べ方を円順列っていうんだ。
今回は人を並べるってことで話をするけど、ものを並べる場合も同じだから、まずは人を並べる円順列の解き方をマスターしよう。
ただ人は区別がつくよね。今回は区別がつくものを円形に並べる並べ方の学習で、区別がつかないものを円形に並べるのはまた別の話になるからね。その場合は次の記事をチェックしておこう。
円順列
\(\small{ \ \displaystyle\frac{n!}{n}={}_{n-1}\mathrm{P}_{n-1}=(n-1)! \ }\)
円順列と順列の違い
\(\small{ \ n \ }\)人の円順列がどうして\(\small{ \ (n-1)! \ }\)になるのか考えてみよう。
それは下の図の右も左も同じ\(\small{ \ 1 \ }\)通りって考えるからなんだ。回転させただけで並び変えていないのに気付くよね。
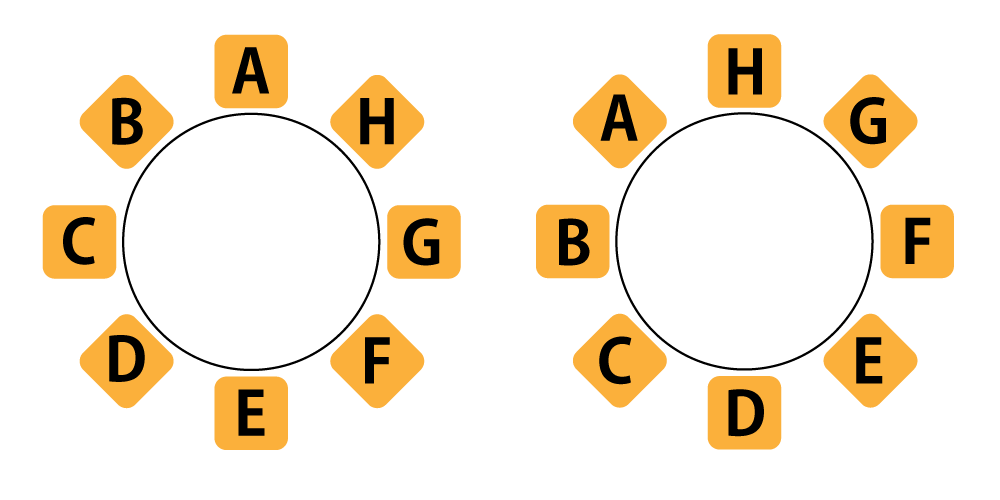
つまり円順列っていうのは隣や向かいとか全て同じ並びだったら、同じ並び方って考えるんだ。場所は関係ないってことね。
\(\small{ \ a_1~a_n \ }\)の\(\small{ \ n \ }\)個を一列に並べる順列の場合
\(\small{ \ n \ }\)通り\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
a_1,a_2,a_3,a_4,a_5,\cdots,a_{n-1},a_n\\
a_2,a_3,a_4,a_5,a_6,\cdots,a_n,a_1\\
a_3,a_4,a_5,a_6,a_7,\cdots,a_1,a_2\\
\qquad \qquad \vdots\\
a_n,a_1,a_2,a_3,a_4,\cdots,a_{n-2},a_{n-1}\end{array}
\right.
\end{eqnarray} \ }\)
この\(\small{ \ n \ }\)通りの並びも、これを円形に並べて円順列にすると、順序が変わらないから\(\small{ \ 1 \ }\)通りになるよね。
だから\(\small{ \ n \ }\)人の場合、一列に並んで\(\small{ \ n! \ }\)ってなる順列を円順列にするためには\(\small{ \ n \ }\)で割る必要があるんだ。
つまり\(\small{ \ \displaystyle\frac{n!}{n}={}_{n-1}\mathrm{P}_{n-1}=(n-1)! \ }\)通りになるからね。
円順列の考え方
円順列は\(\small{ \ n \ }\)人並べるときは\(\small{ \ n \ }\)で割ればいいってことは分かったんだけど、区別が付かないものを並べたりすると、少し話が変わってくるよね。
そういう時も困らないように、\(\small{ \ n \ }\)で割る以外のパターンがある。っていうかこっちのほうが基本的な考え方になるかな。
それは\(\small{ \ 1 \ }\)人固定して、それ以外を並べるってこと。
図のように\(\small{ \ \mathrm{A} \ }\)を固定して、それ以外を順列として並べるってことね。
そうすると\(\small{ \ n \ }\)人を並べるときは\(\small{ \ 1 \ }\)人固定して、それ以外の\(\small{ \ (n-1) \ }\)人を並べたらいいよね。
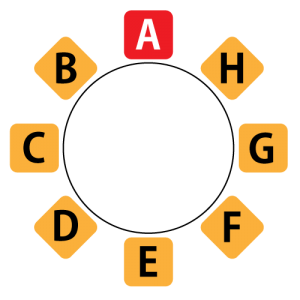
つまり\(\small{ \ (n-1) \ }\)人の順列になるから\(\small{ \ (n-1)! \ }\)通りってなるよね。
ただ、このとき注意しておきたいのが、固定する人は誰でもいいから\(\small{ \ 1 \ }\)人だけってこと。
\(\small{ \ \mathrm{A} \ }\)を固定して考えた後に、次に\(\small{ \ \mathrm{B} \ }\)を固定してって考えると重なる並びができるから、固定するのは\(\small{ \ 1 \ }\)人だけ。
でも問題文によって固定する人を指定した方が簡単だから、問題文から固定する人を選ぼう。
例えば男子\(\small{ \ 2 \ }\)人と女子が数人並ぶような問題で、男子が向かい合うって場合、男子の\(\small{ \ 1 \ }\)人を固定することで、もう\(\small{ \ 1 \ }\)人の男子もその向かい並ぶことになるよね。
問題文によって誰を固定したらいいか考えていこう。
上座と下座
円順列って並びが同じだったら回転しても同じ並びって数えるんだよね。
でも実際は円形のテーブルに座るって考えた場合、窓やドアがあるから、席に区別があるよね。
席の区別を考えたら円順列じゃなくて、順列になるから注意しよう。
図は入口を書き加えただけなんだけど、それだけで席に区別が付くから、もう円順列じゃなくなるよね。
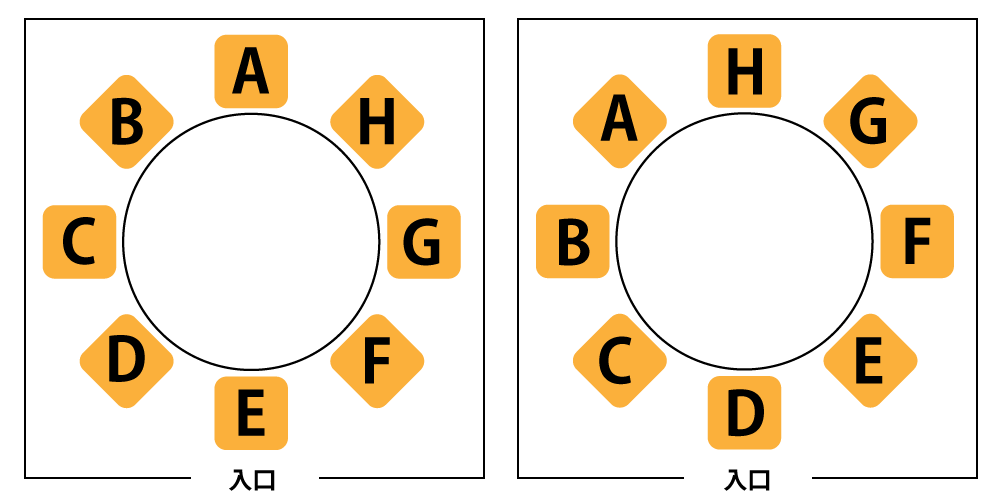
ここからは余談になるけど、一般的な席には上座や下座って席の区別があって、入口から遠いほうが上座になったり、景色がいい席が上座になったりするんだ。
さらに上座には役職が高い人が座るし、接待なんかだと接待する側が下座、接待される側が上座になるのが一般的なんだ。
受験や勉強には関係ないけど知識として知っておくといいかもね。
話が脱線したけど、結局何が言いたかったかっていうと高校数学で学習する円順列は周りの景色を考慮しない順列の学習ってのがほとんどになるってこと。ここのところをよく押さえておこう。
周りの景色を考慮したら、円順列じゃなくて順列になるからね。実はここをよく理解していない人が多いから注意しよう。
大人\(\small{ \ 2 \ }\)人、子供\(\small{ \ 8 \ }\)人が円形のテーブルに座るとき、次のような並び方は何通りあるか求めよ。
(1)自由に座る
(2)大人が隣り合う
(3)大人が向かい合う
(1)\(\small{ \ (10-1)!=362880 \ }\)
(2)大人\(\small{ \ 2 \ }\)人を\(\small{ \ 1 \ }\)組として、\(\small{ \ 9 \ }\)人の円順列に大人の並び方が\(\small{ \ 2 \ }\)通りある
\(\small{ \ (9-1)!\times2=80640 \ }\)
(3)\(\small{ \ 1 \ }\)人の大人を固定すると、もう\(\small{ \ 1 \ }\)人の大人の位置も決まり、残り子供\(\small{ \ 8 \ }\)人並べればいい
\(\small{ \ 8!=40320 \ }\)

Point 円順列
①\(\small{ \ n \ }\)人の円順列は\(\small{ \ (n-1)! \ }\)
②問題文から固定する人を考える
\(\small{ \ \mathrm{A} \ }\)さんとその\(\small{ \ 3 \ }\)人の子供、\(\small{ \ \mathrm{B} \ }\)さんとその\(\small{ \ 3 \ }\)人の子供、\(\small{ \ \mathrm{C} \ }\)さんとその\(\small{ \ 2 \ }\)人の子供の合わせて\(\small{ \ 11 \ }\)人が、\(\small{ \ \mathrm{A} \ }\)さんと\(\small{ \ \mathrm{A} \ }\)さんの末っ子は隣り合わせになるようにして、円形のテーブルに座る。\(\small{ \ \def\cenBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ }}\def\cenbox#1{\bbox[4px, border:1px solid gray]{\ #1\ }} \ }\)
このとき、それぞれの家族がまとまって座る場合の座り方は\(\small{ \ \cenbox{ア} \ }\)通りあり、その中で異なる家族の子供たちが隣り合わせにならないような座り方は\(\small{ \ \cenbox{イ} \ }\)通りある。
(ア)それぞれの家族がまとまって座るので、それぞれを\(\small{ \ 1 \ }\)組と考えた円順列は
\(\small{ \ (3-1)!=2 \ }\)通り
その中で\(\small{ \ \mathrm{A} \ }\)さん家族が一列に並ぶ並び方は\(\small{ \ \mathrm{A} \ }\)さんと末っ子が隣り合うことを考えて
\(\small{ \ 3!\times2!=12 \ }\)通り
\(\small{ \ \mathrm{B} \ }\)さん家族が一列に並ぶ並び方は
\(\small{ \ 4!=24 \ }\)通り
\(\small{ \ \mathrm{C} \ }\)さん家族が一列に並ぶ並び方は
\(\small{ \ 3!=6 \ }\)通り
よって求める座り方は
\(\small{ \ 2\times12\times24\times6=3456 \ }\)通り
(イ)異なる家族の子供が隣り合わないということは、異なる家族の子供の間に大人が入るということになる。
大人は\(\small{ \ 3 \ }\)人なので、その大人の間①〜③の\(\small{ \ 3 \ }\)箇所に、各家族の子供がまとまって並べばいい。
また\(\small{ \ \mathrm{A} \ }\)さんの隣に\(\small{ \ \mathrm{A} \ }\)さんの末っ子が座ることになる。
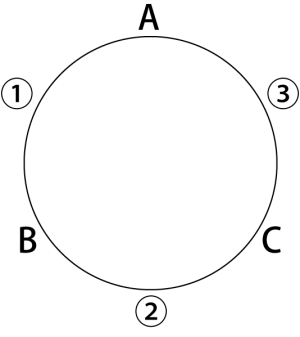
①に\(\small{ \ \mathrm{A} \ }\)さんの子供たちが座るとき、
\(\small{ \ \mathrm{B} \ }\)さんと\(\small{ \ \mathrm{C} \ }\)さんの並び方が\(\small{ \ 2! \ }\)通り、\(\small{ \ \mathrm{B} \ }\)さんの子供たちと\(\small{ \ \mathrm{C} \ }\)さんの子供たちが②と③に並ぶ並び方が\(\small{ \ 2! \ }\)通り
①に並ぶAさんの子供たちの並び方が\(\small{ \ 2! \ }\)通り、
②または③にならぶ\(\small{ \ \mathrm{B} \ }\)さんの子供たちの並び方が\(\small{ \ 3! \ }\)通り、
\(\small{ \ \mathrm{C} \ }\)さんの子供たちの並び方が\(\small{ \ 2! \ }\)通り
\(\small{ \ 2!\times2!\times2!\times3!\times2!=48 \ }\)通り
\(\small{ \ \mathrm{A} \ }\)さんの子供たちが③に座るときも同じ
よって求める座り方は
\(\small{ \ 48\times2=96 \ }\)通り

