三角形の外角の二等分線と線分比

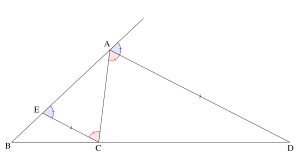
\(\small{ \ \mathrm{C} \ }\)を通り\(\small{ \ \mathrm{AD} \ }\)に平行な直線と直線\(\small{ \ \mathrm{AB} \ }\)との交点を\(\small{ \ \mathrm{E} \ }\)、直線\(\small{ \ \mathrm{AB} \ }\)の\(\small{ \ \mathrm{A} \ }\)の先を\(\small{ \ \mathrm{O} \ }\)とすると、
\(\small{ \ \mathrm{AD} /\!/ \mathrm{CE} \ }\)より
\(\small{ \ \angle \mathrm{OAD}=\angle \mathrm{AEC} \ }\)（同位角）
\(\small{ \ \angle \mathrm{DAC}=\angle \mathrm{ACE} \ }\)（錯角）
\(\small{ \ \mathrm{AD} \ }\)は外角の二等分線より
\(\small{ \ \angle \mathrm{OAD}=\angle \mathrm{DAC} \ }\)
\(\small{ \ \therefore \angle \mathrm{AEC}=\angle \mathrm{ACE} \ }\)
よって\(\small{ \ \triangle \mathrm{ACE} \ }\)は二等辺三角形
\(\small{ \ \mathrm{AC}=\mathrm{AE} \ }\)
\(\small{ \ \triangle \mathrm{BEC} \backsim \triangle \mathrm{BAD} \ }\)より
\(\small{ \ \mathrm{AB}:\mathrm{AE}=\mathrm{BD}:\mathrm{CD} \ }\)
\(\small{ \ \mathrm{AC}=\mathrm{AE} \ }\)より
\(\small{ \ \mathrm{AB}:\mathrm{AC}=\mathrm{BD}:\mathrm{CD} \ }\)

高さが等しいので
\(\small{ \ \mathrm{BD}:\mathrm{CD}=\triangle \mathrm{ABD}:\mathrm{ACD} \ }\)
ここで\(\small{ \ \angle \mathrm{CAD}=\left(180^{ \circ }-\angle \mathrm{A}\right)\cdot \displaystyle \frac{1}{2}=90^{ \circ }- \displaystyle \frac{\mathrm{A}}{2} \ }\)
\(\small{\begin{eqnarray} \ \triangle \mathrm{ABD}&=& \displaystyle \frac{1}{2} \mathrm{AB}\cdot \mathrm{AD} \sin\left(90^{ \circ }+ \displaystyle \frac{\mathrm{A}}{2}\right)\\
&=&\displaystyle \frac{1}{2} \mathrm{AB}\cdot \mathrm{AD} \cos \displaystyle \frac{\mathrm{A}}{2} \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ \triangle \mathrm{ACD}&=& \displaystyle \frac{1}{2} \mathrm{AD}\cdot \mathrm{AC} \sin\left(90^{ \circ }-\displaystyle \frac{\mathrm{A}}{2}\right)\\
&=&\displaystyle \frac{1}{2} \mathrm{AC}\cdot \mathrm{AD} \cos \displaystyle \frac{\mathrm{A}}{2} \ \end{eqnarray}}\)
\(\small{ \ \triangle \mathrm{ABD}:\mathrm{ACD}=\mathrm{AB}: \mathrm{AC} \ }\)
よって\(\small{ \ \mathrm{AB}:\mathrm{AC}=\mathrm{BD}:\mathrm{CD} \ }\)