こんにちは、リンス(@Lins016)です。
今回は平面ベクトルの成分表示とその解き方について学習していこう。
ベクトルの成分表示とは
ベクトルとは大きさと向きがあるものだったよね。これをよりわかりやすくしたものに成分表示したベクトルがある。
これは\(\small{ \ xy \ }\)平面上にベクトルを置いた考え方で、そのベクトルが\(\small{ \ x \ }\)方向、\(\small{ \ y \ }\)方向にそれぞれどれくらい移動したかの移動量を表したものになる。
\(\small{ \ \vec{a}=(a_1, \ a_2) \ }\)って書くんだけど、点の座標とはちょっと違うから覚えておこう。
ベクトルは平行移動しても同じベクトルになるから、原点の位置を始点とすれば点\(\small{ \ (a_1, \ a_2) \ }\)を終点とするベクトルになるけど、始点が原点以外の点なら終点は点\(\small{ \ (a_1, \ a_2) \ }\)にならないからね。
点\(\small{ \ (a_1, \ a_2) \ }\)なのか\(\small{ \ \vec{a}=(a_1, \ a_2) \ }\)なのか同じ書き方だからわかりにくいけど、実際は問題を読めば点のことを言っているのか、ベクトルのことを言っているのかはすぐわかるから間違えることはないと思う。

ベクトルの成分表示とその解き方
まず頭に入れておいて欲しいことがある。
それは「問題文が成分表示のときは成分表示を利用して解く」ということ。
問題が成分表示のベクトルで書いてあるのに、わざわざ文字で表記するベクトル(\(\small{ \ \overrightarrow{ \mathrm{OA} } \ }\)や\(\small{ \ \vec{a} \ }\))で問題を解いたりしないようにね。
成分表示のベクトルの問題は成分表示のまま解こう。
成分表示されたベクトルの実数倍
ベクトルを伸ばしたり縮めたりする場合、実数\(\small{ \ k \ }\)を使って\(\small{ \ k \vec{a} \ }\)ってかくことができたよね。
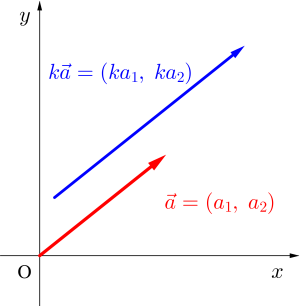
成分表示の場合は\(\small{ \ \vec{a}=(a_1, \ a_2) \ }\)を\(\small{ \ k \ }\)倍すると
\(\small{ \ k\vec{a}=k(a_1, \ a_2)=(ka_1, \ ka_2) \ }\)になる。
これは図をみても明らかだよね。
成分表示されたベクトルの和
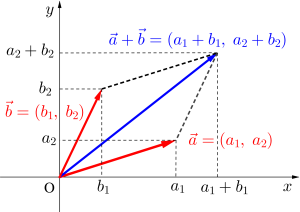
成分表示された二つのベクトル\(\small{ \ \vec{a}=(a_1, \ a_2) \ }\)と\(\small{ \ \vec{b}=(b_1, \ b_2) \ }\)の和について考えてみよう。
成分表示のベクトルの場合\(\small{ \ x \ }\)成分と\(\small{ \ y \ }\)成分をそれぞれ足せばいいから
\(\small{\begin{eqnarray} \ \vec{a}+\vec{b}&=&(a_1, \ a_2)+(b_1, \ b_2)\\
&=&(a_1+b_1, \ a_2+b_2) \ \end{eqnarray}}\)
になる。
図で見ても明らかだよね。
これを前回のベクトルの基本でも学習した「基準のベクトルの二つを用いて他のベクトルを表す」ってことを考えてみよう。
\(\small{ \ \overrightarrow{ \mathrm{OP} }=s \overrightarrow{ \mathrm{OA} }+t \overrightarrow{ \mathrm{OB} } \ }\)だったから
\(\small{ \ \overrightarrow{ \mathrm{OP} }=(x, \ y) \ }\)とすると
\(\small{\begin{eqnarray} \ (x, \ y)&=&s(a_1, \ a_2)+t(b_1, \ b_2)\\
&=&(sa_1+tb_1, \ sa_2+tb_2) \ \end{eqnarray}}\)
になる。
基本的に二つの基準のベクトルは問題文から与えられているから、その他のベクトルも\(\small{ \ s, \ t \ }\)の実数を利用することで成分で表示することができる。
\(\small{ \ s, \ t \ }\)二つの実数を利用することですべての平面ベクトルを表すことができるけど、問題を解くってなったら何かしらの条件があるはずだから、二つの実数ではなく、一つの実数だけでベクトルを表示することがほとんどになるけどね。
成分表示されたベクトルの差
今度は成分表示された二つのベクトル\(\small{ \ \vec{a}=(a_1, \ a_2) \ }\)と\(\small{ \ \vec{b}=(b_1, \ b_2) \ }\)の差について考えてみよう。
成分表示のベクトルの場合\(\small{ \ x \ }\)成分と\(\small{ \ y \ }\)成分をそれぞれ引けばいいから
\(\small{\begin{eqnarray} \ \vec{a}-\vec{b}&=&(a_1, \ a_2)-(b_1, \ b_2)\\
&=&(a_1-b_1, \ a_2-b_2) \ \end{eqnarray}}\)
になる。
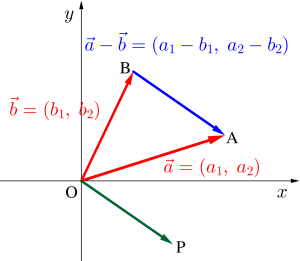
ここで注意しておきたいのが、この求めた成分は\(\small{ \ x \ }\)方向、\(\small{ \ y \ }\)方向にそれぞれどれくらい移動したかの移動量だから、イメージとしては原点から見た成分になるってこと。
ベクトルは平行移動しても同じベクトルだから図のように\(\small{ \ \overrightarrow{ \mathrm{OP} }= \overrightarrow{ \mathrm{AB} } \ }\)がいえる。
つまり求めた\(\small{ \ \vec{a}-\vec{b}=(a_1-b_1, \ a_2-b_2) \ }\)は\(\small{ \ \overrightarrow{ \mathrm{AB} } \ }\)なんだけど、成分表示では\(\small{ \ \overrightarrow{ \mathrm{OP} } \ }\)の原点を始点として点\(\small{ \ \mathrm{P} \ }\)を終点としたベクトルが表されるってことを頭に入れておこう。
成分表示されたベクトルの大きさ
成分表示されたベクトル\(\small{ \ \vec{a}=(a_1, \ a_2) \ }\)の大きさについて考えてみよう。
成分表示されたベクトルの大きさは三平方の定理定理を利用すると簡単に求めることができる。
成分表示は\(\small{ \ x \ }\)成分と\(\small{ \ y \ }\)成分の移動量を表しているから、それぞれの値を\(\small{ \ 2 \ }\)乗して足せば、そのベクトルの大きさの\(\small{ \ 2 \ }\)乗になる。
\(\small{ \ \therefore | \vec{a}|= \sqrt{{a_1}^2+{a_2}^2} \ }\)
\(\small{ \ \vec{a}+\vec{b}=(a_1+b_1, \ a_2+b_2) \ }\)の大きさは
\(\small{ \ |\vec{a}+\vec{b}|=\sqrt{(a_1+b_1)^2+ (a_2+b_2)^2} \ }\)になる。

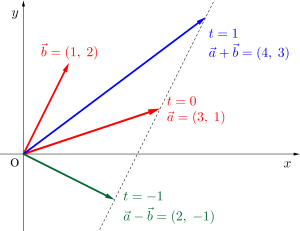
\(\small{ \ \vec{a}=(3, \ 1) \ }\)、\(\small{ \ \vec{b}=(1, \ 2) \ }\)のとき、\(\small{ \ \vec{c}= \vec{a}+t \vec{b} \ }\)(\(\small{ \ t \ }\)は実数)について考える。
(1)\(\small{ \ | \vec{c}|= \sqrt{15} \ }\)のとき、\(\small{ t \ }\)の値を求めよ。
(2)\(\small{ \ | \vec{c}| \ }\)の最小値とそのときの\(\small{ \ t \ }\)の値を求めよ。
\(\small{ \ \vec{c}=(3, \ 1)+t(1, \ 2)=(t+3, \ 2t+1) \ }\)
\(\small{\begin{eqnarray} \ | \vec{c}|&=& \sqrt{(t+3)^2+(2t+1)^2}\\
&=& \sqrt{5t^2+10t+10} \ \end{eqnarray}}\)
(1)
\(\small{ \ | \vec{c}|= \sqrt{15} \ }\)より
\(\small{ \ \sqrt{5t^2+10t+10}= \sqrt{15} \ }\)
\(\small{ \ 5t^2+10t-5=0 \ }\)
\(\small{ \ t^2+2t-1=0 \ }\)
\(\small{ \ \therefore t=-1\pm \sqrt{2} \ }\)
(2)
\(\small{ \ | \vec{c}|=\sqrt{5t^2+10t+10}\\
=\sqrt{5(t+1)^2+5} \ }\)
よって\(\small{ \ t=-1 \ }\)のとき最小で\(\small{ \ | \vec{c}|= \sqrt{5} \ }\)


これは\(\small{ \ \vec{c}=(t+3, \ 2t+1) \ }\)からも媒介変数の軌跡とも言えるよね。
Point ベクトルの成分表示とその解き方
①ベクトルの成分表示の問題は成分表示のまま解こう
②成分表示されたベクトルの和や差、実数倍を丁寧に計算して新しいベクトルを成分表示しよう

