こんにちは、リンス(@Lins016)です。
今回は放物線と直線の共有点(二次関数と一次関数の共有点(交点))の求め方について学習していこう。
放物線と直線の共有点(交点)
放物線と直線の共有点を求める問題って確実にできないといけないよ。二次関数だけじゃなくて、三次関数を扱う微分積分でも出題されるからね。
もちろん放物線と直線の位置関係によっては共有点を持たない場合もある。特に直線が\(\small{ \ y=2x+a \ }\)のような定数を含む場合は定数\(\small{ \ a \ }\)の値によって放物線と直線の共有点の個数も変化するから注意しよう。
\(\small{ \ y=ax^2+bx+c \ }\)と\(\small{ \ y=mx+n \ }\)の共有点の座標
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
y=ax^2+bx+c\\
y=mx+n\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ y \ }\)を消去して
\(\small{ \ ax^2+bx+c=mx+n \ }\)を解けば良い
放物線と直線の共有点(交点)の求め方
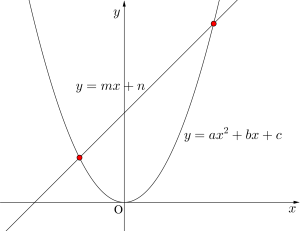
放物線と直線の共有点はその\(\small{ \ 2 \ }\)つの式を連立して共有点の座標を求めよう。
放物線は二次関数、直線は一次関数だから直線の式を\(\small{ \ y=mx+n \ }\)の形に変形して二次関数\(\small{ \ y=ax^2+bx+c \ }\)に代入して、\(\small{ \ ax^2+bx+c=mx+n \ }\)。これから二次方程式\(\small{ \ ax^2+(b-m)x+c-n=0 \ }\)が作れるからその二次方程式を解いて共有点の\(\small{ \ x \ }\)座標を求めよう。
\(\small{ \ x \ }\)座標が求まったら直線の方程式に代入して\(\small{ \ y \ }\)座標も求めよう。
放物線の式に代入しても同じ値になるけど、簡単な式に代入したほうが計算ミスがなくなるから、直線の一次関数の式に代入しよう。
-

二次方程式の解き方
二次方程式の解き方について学習します。因数分解や解の公式の利用、文字を含んだ二次方程式の解き方について解説しています。
続きを見る
放物線と直線の共有点の個数
放物線と直線が常に交わるかといえばそうじゃないよね。放物線と直線の位置関係によっては交わったり、接したり、交わらなかったりもする。
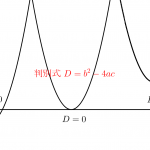
これは放物線と直線の式を連立させた二次方程式の解の個数で位置関係を判断することができる。二次方程式の解の個数を調べるっていったら判別式だよね。
解がそのまま求められるような式だったら、解の公式や因数分解を利用して解けばいいけど、定数が含まれている場合は、定数の範囲によって解の個数が変わるから判別式を利用して定数の範囲を場合分けしないといけないからね。
-

判別式とその利用
判別式について学習してます。解の個数や、グラフとx軸の共有点の数の求め方、不等式の作成について解説しています。
続きを見る
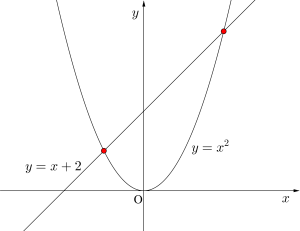
(1)\(\small{ \ y=x^2 \ }\)と\(\small{ \ y=x+2 \ }\)の共有点の座標を求めよ。
(2)\(\small{ \ y=x^2 \ }\)と\(\small{ \ y=2x+a \ }\)が接するとき、共有点の座標を求めよ。
(1)\(\small{ \ x^2=x+2 \ }\)
\(\small{ \ x^2-x-2=0 \ }\)
\(\small{ \ (x-2)(x+1)=0 \ }\)
\(\small{ \ x=-1, \ 2 \ }\)
\(\small{ \ y=-1+2=1 \ }\)
\(\small{ \ y=2+2=4 \ }\)
よって共有点の座標は\(\small{ \ (-1, \ 1), \ (2, \ 4) \ }\)
(2)\(\small{ \ x^2=2x+a \ }\)
\(\small{ \ x^2-2x-a=0 \ }\)
\(\small{ \ D=4+4a=0 \ }\)
\(\small{ \ a=-1 \ }\)
\(\small{ \ x^2-2x+1=0 \ }\)
\(\small{ \ (x-1)^2=0 \ }\)
\(\small{ \ x=1 \ }\)
\(\small{ \ y=2\cdot1-1=1 \ }\)
よって共有点の座標は\(\small{ \ (1, \ 1) \ }\)


Point 放物線と直線の共有点の求め方
①放物線と直線の共有点の座標は連立方程式から求める
②共有点の個数は判別式を利用して求める
放物線\(\small{ \ y=x^2-5x+6 \ }\)と直線\(\small{ \ y=kax-a^2-5a \ }\)がある
(1)すべての実数\(\small{ \ a \ }\)に対して放物線と直線が異なる\(\small{ \ 2 \ }\)点で交わるような定数\(\small{ \ k \ }\)の値の範囲を求めよ。
(2)(1)で求めた範囲にあって放物線と直線の共有点の\(\small{ \ x \ }\)座標の差が\(\small{ \ a \ }\)の値によらず一定になるような定数\(\small{ \ k \ }\)の値を求めよ。
(1)放物線と直線を連立して
\(\small{ \ x^2-5x+6=kax-a^2-5a \ }\)
\(\small{ \ x^2-(ka+5)x+a^2+5a+6=0 \ }\)
放物線と直線が異なる\(\small{ \ 2 \ }\)点で交わるから
\(\small{ \ D_1=(ka+5)^2-4(a^2+5a+6)\gt0 \ }\)
\(\small{ \ (k^2-4)a^2+(10k-20)a+1 \gt0 \ }\)
これが全ての実数\(\small{ \ a \ }\)で成り立てばよいので
(i)\(\small{ \ k^2-4\gt0 \ }\)かつ\(\small{ \ D_2=(10k-20)^2-4(k^2-4) \lt 0 \ }\)
または(ii)\(\small{ \ k^2-4=0 \ }\)かつ\(\small{ \ 10k-20=0 \ }\)
(i)のとき
\(\small{ \ k^2-4\gt0 \ }\)\(\small{ \ \therefore k\lt-2, \ k\gt2\cdots① \ }\)
\(\small{ \ D_2=(10k-20)^2-4(k^2-4) \lt 0 \ }\)
\(\small{ \ 6k^2-25k+26\lt 0 \ }\)
\(\small{ \ (6k-13)(k-2)\lt0 \ }\)
\(\small{ \ \therefore 2 \lt k \lt \displaystyle \frac{13}{6}\cdots② \ }\)
\(\small{ \ ①, \ ② \ }\)より
\(\small{ \ 2 \lt k \lt \displaystyle \frac{13}{6} \ }\)
(ii)のとき
\(\small{ \ k^2-4=0 \ \therefore k=\pm2 \ }\)
\(\small{ \ 10k-20=0 \ \therefore k=2 \ }\)
よって\(\small{ \ k=2 \ }\)
(i)(ii)より
\(\small{ \ 2 \leqq k \lt \displaystyle \frac{13}{6} \ }\)
(2)\(\small{ \ x \ }\)座標の差は
\(\small{ \ x^2-(ka+5)x+a^2+5a+6=0 \ }\)の解の差なので
解を\(\small{ \ x=\alpha, \ \beta \ }\)とすると
解と係数の関係から
\(\small{ \ \alpha+\beta=ka+5, \ \alpha\beta=a^2+5a+6 \ }\)
解の差はこれを利用すると
&=&(ka+5)^2-4(a^2+5a+6)\\
&=&(k^2-4)a^2+(10k-20)a+1\ \end{eqnarray}}\)
これが\(\small{ \ a \ }\)の値によらず一定になるためには
\(\small{ \ k^2-4=0 \ }\)かつ\(\small{ \ 10k-20=0 \ }\)
よって\(\small{ \ k=2 \ }\)