位置ベクトルの基本と内分点・外分点の位置ベクトル

こんにちは、リンス(@Lins016)です。
今回は位置ベクトルの基本と内分点・外分点の位置ベクトルについて学習していこう。

内分点と外分点の位置ベクトルの表示

平面ベクトルに限らず空間ベクトルでもある二点の内分点や外分点をベクトルで表すっていうのはベクトルの中で最頻出って言ってもいい。

簡単な公式だけど、正確に理解しておこう。

位置ベクトルとは

位置ベクトルとは原点\(\small{ \ \mathrm{O} \ }\)と点\(\small{ \ \mathrm{P} \ }\)を結んだベクトル\(\small{ \ \overrightarrow{\mathrm{OP}} \ }\)のことで、点\(\small{ \ \mathrm{P} \ }\)が原点に対してどんな位置にあるかをベクトルで表したものになるんだ。

別に原点が基準点じゃなくてもいいから、三角形\(\small{ \ \triangle\mathrm{ABC} \ }\)のときは点\(\small{ \ \mathrm{A} \ }\)を基準点にしよう。

位置ベクトルの記号

まずは記号に慣れよう。

よく問題文に「\(\small{ \ \mathrm{A}(\overrightarrow{a}) \ }\)、\(\small{ \ \mathrm{B}(\overrightarrow{b}) \ }\)のとき」って書いてある。
これは原点\(\small{ \ \mathrm{O} \ }\)が始点で点\(\small{ \ \mathrm{A} \ }\)が終点のベクトル\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)を\(\small{ \ \overrightarrow{a} \ }\)とするってことを表してるんだ。

もちろん原点の位置は書いてないから原点をどこにあってもよくて、図のように点\(\small{ \ \mathrm{A} \ }\)と点\(\small{ \ \mathrm{B} \ }\)に対して、原点が\(\small{ \ \mathrm{O_1} \ }\)の位置なら\(\small{ \ \overrightarrow{a} \ }\)、\(\small{ \ \overrightarrow{b} \ }\)は赤いベクトルになるし、原点が\(\small{ \ \mathrm{O_2} \ }\)の位置なら\(\small{ \ \overrightarrow{a} \ }\)、\(\small{ \ \overrightarrow{b} \ }\)は青いベクトルになる。

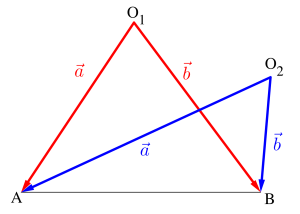
これだとベクトルの長さや向き、二つのベクトルのなす角が違うよね。
だけど、違っても構わないんだ。

位置ベクトルを利用する問題は、点\(\small{ \ \mathrm{A} \ }\)と点\(\small{ \ \mathrm{B} \ }\)の位置に対して、これから求める点\(\small{ \ \mathrm{P} \ }\)がどこにあるかを調べる問題になるから、原点がどこにあっても関係ないし、ベクトルの大きさやなす角も必要ないんだ。

ベクトルの内分点

それじゃベクトルの内分点について考えていこう。
\(\small{ \ \mathrm{A}(\overrightarrow{a}) \ }\)、\(\small{ \ \mathrm{B}(\overrightarrow{b}) \ }\)を\(\small{ \ m:n \ }\)に内分する点\(\small{ \ \mathrm{P}(\overrightarrow{p}) \ }\)のベクトルを考えてみよう。

\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OP}}&=&\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AP}}\\
&=&\overrightarrow{\mathrm{OA}}+\displaystyle\frac{m}{m+n}\overrightarrow{\mathrm{AB}}\\
&=&\overrightarrow{\mathrm{OA}}+\displaystyle\frac{m}{m+n}\left(\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}\right)\\
&=&\displaystyle\frac{n\overrightarrow{\mathrm{OA}}+m\overrightarrow{\mathrm{OB}}}{m+n}\\
&=&\displaystyle\frac{n\overrightarrow{a}+m\overrightarrow{b}}{m+n} \ \end{eqnarray}}\)

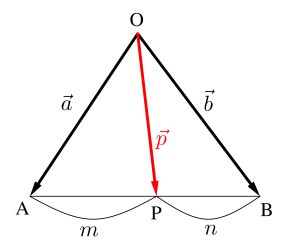
だから\(\small{ \ \mathrm{A}(\overrightarrow{a}) \ }\)、\(\small{ \ \mathrm{B}(\overrightarrow{b}) \ }\)を\(\small{ \ m:n \ }\)に内分する点\(\small{ \ \mathrm{P}(\overrightarrow{p}) \ }\)のベクトルは
\(\small{ \ \overrightarrow{\mathrm{p}}=\displaystyle\frac{n\overrightarrow{a}+m\overrightarrow{b}}{m+n} \ }\)になるんだ。

ベクトルの外分点

次は\(\small{ \ \mathrm{A}(\overrightarrow{a}) \ }\)、\(\small{ \ \mathrm{B}(\overrightarrow{b}) \ }\)を\(\small{ \ m:n \ }\)に外分する点\(\small{ \ \mathrm{P}(\overrightarrow{p}) \ }\)のベクトルを考えてみよう。

\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OP}}&=&\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AP}}\\
&=&\overrightarrow{\mathrm{OA}}+\displaystyle\frac{m}{m-n}\overrightarrow{\mathrm{AB}}\\
&=&\overrightarrow{\mathrm{OA}}+\displaystyle\frac{m}{m-n}\left(\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}\right)\\
&=&\displaystyle\frac{-n\overrightarrow{\mathrm{OA}}+m\overrightarrow{\mathrm{OB}}}{m-n}\\
&=&\displaystyle\frac{-n\overrightarrow{a}+m\overrightarrow{b}}{m+n} \ \end{eqnarray}}\)

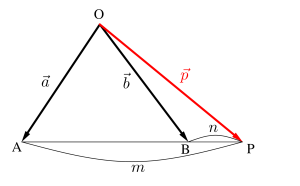
だから\(\small{ \ \mathrm{A}(\overrightarrow{a}) \ }\)、\(\small{ \ \mathrm{B}(\overrightarrow{b}) \ }\)を\(\small{ \ m:n \ }\)に外分する点\(\small{ \ \mathrm{P}(\overrightarrow{p}) \ }\)のベクトルは
\(\small{ \ \overrightarrow{\mathrm{p}}=\displaystyle\frac{-n\overrightarrow{a}+m\overrightarrow{b}}{m+n} \ }\)になるんだ。

\(\small{ \ m\gt n \ }\)のとき、点\(\small{ \ \mathrm{P} \ }\)は半直線\(\small{ \ \mathrm{AB} \ }\)上にあって、\(\small{ \ m\lt n \ }\)のとき、点\(\small{ \ \mathrm{P} \ }\)は半直線\(\small{ \ \mathrm{BA} \ }\)上にあるから注意しよう。

二つの基準のベクトル

平面ベクトルの基本でも話をしたけど、二つの基準のベクトルを用いれば、その他のベクトルは基準のベクトルの実数倍の和、つまり「\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)」の形で表すことができる。

つまり内分や外分によって実数\(\small{ \ s, \ t \ }\)を求めることができるんだ。

ただ、まずは常に基準のベクトルと同じ始点から始まるベクトルに変形して、それぞれの点がどのような点なのか考えていくことが大事になる。

例えば\(\small{ \ \overrightarrow{\mathrm{PQ}}=\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OP}} \ }\)にして、点\(\small{ \ \mathrm{P, \ Q} \ }\)がそれぞれどんな点なのか考えるってことね。

常に基準のベクトルと始点を揃えて問題を考えていこう。

問題解答

\(\small{ \ \triangle\mathrm{ABC} \ }\)の辺\(\small{ \ \mathrm{BC, \ CA} \ }\)を\(\small{ \ 2:3 \ }\)に内分する点をそれぞれ\(\small{ \ \mathrm{D, \ E} \ }\)とし、\(\small{ \ \triangle\mathrm{ABC} \ }\)の重心を\(\small{ \ \mathrm{G} \ }\)とするとき、次のベクトルを\(\small{ \ \overrightarrow{\mathrm{AB}}=\overrightarrow{b}, \ \overrightarrow{\mathrm{AC}}=\overrightarrow{c} \ }\)で表せ。
(1)\(\small{ \ \overrightarrow{\mathrm{AD}} \ }\)
(2)\(\small{ \ \overrightarrow{\mathrm{DE}} \ }\)
(3)\(\small{ \ \overrightarrow{\mathrm{GC}} \ }\)

(1)点\(\small{ \ \mathrm{D} \ }\)は辺\(\small{ \ \mathrm{BC} \ }\)を\(\small{ \ 2:3 \ }\)に内分する点だから
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AD}}&=&\displaystyle \frac{3\overrightarrow{\mathrm{AB}}+2\overrightarrow{\mathrm{AC}}}{5}\\
&=&\displaystyle \frac{3}{5}\overrightarrow{\mathrm{b}}+\displaystyle \frac{2}{5}\overrightarrow{\mathrm{c}} \ \end{eqnarray}}\)

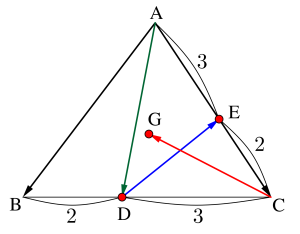
(2)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{DE}}&=&\overrightarrow{\mathrm{AE}}-\overrightarrow{\mathrm{AD}}\\
&=&\displaystyle \frac{3}{5}\overrightarrow{\mathrm{AC}}-\left(\displaystyle \frac{3\overrightarrow{\mathrm{AB}}+2\overrightarrow{\mathrm{AC}}}{5} \right)\\
&=&-\displaystyle \frac{3}{5}\overrightarrow{\mathrm{AB}}+\displaystyle \frac{1}{5}\overrightarrow{\mathrm{AC}}\\
&=&-\displaystyle \frac{3}{5}\overrightarrow{b}+\displaystyle \frac{1}{5}\overrightarrow{c} \ \end{eqnarray}}\)

(3)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{GC}}&=&\overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{AG}}\\
&=&\overrightarrow{\mathrm{AC}}-\displaystyle \frac{\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}}{3}\\
&=&-\displaystyle \frac{1}{3}\overrightarrow{b}+\displaystyle \frac{2}{3}\overrightarrow{c} \ \end{eqnarray}}\)

基準となるベクトル\(\small{ \ \overrightarrow{\mathrm{AB}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{AC}} \ }\)が与えられている場合、すべてのベクトルを\(\small{ \ \mathrm{A} \ }\)を始点とするベクトルで表して、そこから各ベクトルがどのような内分点になっているか考えていこう。

例えば\(\small{ \ \overrightarrow{\mathrm{MN}}=\overrightarrow{\mathrm{AN}}-\overrightarrow{\mathrm{AM}} \ }\)にして、点\(\small{ \ \mathrm{M, \ N} \ }\)がどんな点なのか考えるってことね。

Point　位置ベクトルの基本と内分点・外分点の位置ベクトル

①内分・外分のベクトルの式をしっかりと覚えておこう
②基準のベクトルと始点を揃えてから各点がどんな点なのか考えよう