こんにちは、リンス(@Lins016)です。
今回は三角関数の角の拡張について学習していこう。
弧度法と三角関数
数学Iの図形と計量の三角比では\(\small{ \ 0^{\circ} \ }\)から\(\small{ \ 180^{\circ} \ }\)までいわゆる三角形の角度を取り扱っていたけど、数学Ⅱの三角関数では\(\small{ \ 180^{\circ} \ }\)より大きい角も取り扱っていくんだ。
だから覚える三角関数の値も多いけどきちんと覚えていこう。
・一般角
\(\small{ \ \theta +2n\pi \ }\)(\(\small{ \ n \ }\)は整数)
・度数法から弧度法への変形
\(\small{ \ \alpha^{\circ}→\displaystyle \frac{\alpha^{\circ}}{180^{\circ}}\times \pi \ }\)
・中心角\(\small{ \theta}\)、半径\(\small{ \ r \ }\)の扇型の弧の長さ\(\small{ \ l \ }\)と面積\(\small{ \ \mathrm{S} \ }\)
\(\small{ \ l=r\theta \ }\)
\(\small{ \ \mathrm{S}=\displaystyle \frac{1}{2}r^2\theta \ }\)
一般角と動径
点\(\small{ \ \mathrm{O} \ }\)を中心に半直線\(\small{ \ \mathrm{OP} \ }\)を回転させるとき、この半直線を動径っていうんだ。
動径の最初の位置を始線っていって、始線から動径が反時計回りに回転する方向を正の向き、時計回りに回転する方向を負の向きに定義する。
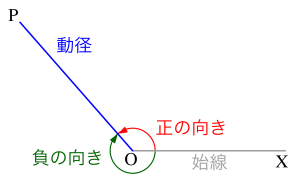
この回転の向きと大きさを持つものを一般角っていって、始線\(\small{ \ \mathrm{OX} \ }\)から\(\small{ \ \theta \ }\)だけ回転した位置にある動径のことを\(\small{ \ \theta \ }\)の動径っていうからね。
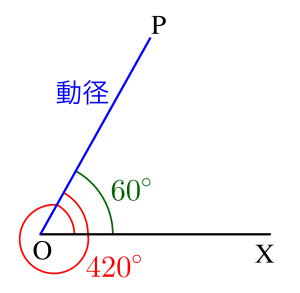
次の図を見てみよう。
この動径は\(\small{ \ 60^{\circ} \ }\)とも\(\small{ \ 420^{\circ} \ }\)ともいえるよね。
動径は\(\small{ \ 360^{\circ} \ }\)回転すると同じ位置になるから、動径と始線のなす角の一つを\(\small{ \ \alpha \ }\)とすると、その表す角は
\(\small{ \ \alpha+360^{\circ}\times n \ }\)って表すことができる。このとき\(\small{ \ n \ }\)は整数だからね。
弧度法とは
数学Iでの学習した三角比では度(\(\small{ \ ^{\circ} \ }\))を単位とする度数法で表された角を利用してきたけど、数学Ⅱではrad(ラジアン)を単位とする弧度法で表された角を利用するからね。
でも急に度数法を弧度法にするのって難しいよね。だから次の式を覚えておこう。
度数法を弧度法に変形
\(\small{ \ \alpha^{\circ}→\displaystyle \frac{\alpha^{\circ}}{180^{\circ}}\times \pi \ }\)
三角比の値も弧度法の値も急に覚えるのは難しいから、まだ弧度法の有名角を覚えていない人は、まず三角比の値とこの度数法を弧度法に変形する式を覚えておこう。
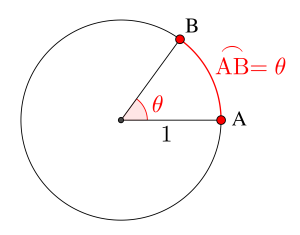
ちなみに円周は直径\(\small{\times \pi \ }\)って教わったよね。だから単位円(半径\(\small{ \ 1 \ }\)の円)の円周は\(\small{ \ 2\pi \ }\)だよね。
この場合、中心角も弧度法では\(\small{ \ 2\pi \ }\)になる。
つまり、弧の長さで角を表す方法が弧度法なんだ。
\(\small{ \ \theta (\mathrm{rad}) \ }\)っていうのは単位円の弧の長さが\(\small{ \ \theta \ }\)になる角度ってことなんだ。
慣れてくると度数法より弧度法の方が理にかなってる感じがするよね。
だって一周がなぜ\(\small{ \ 360^{\circ} \ }\)で定義されてるのかよくわからないよね。別に\(\small{ \ 300^{\circ} \ }\)で定義しても良かったんじゃないのってね笑。
でも弧度法は単位円の円周の長さが\(\small{ \ 2\pi \ }\)だからその角を\(\small{ \ 2\pi \ }\)で定義したってことだもんね。こっちの方が数学的だよね。
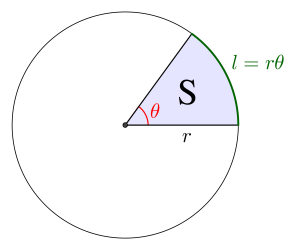
弧度法による扇型の弧の長さと面積
扇型の弧の長さは直径\(\small{\times \pi \times \displaystyle \frac{中心角}{360^{\circ}} \ }\)だったよね。
これを半径\(\small{ \ r \ }\)、中心角\(\small{ \ \theta \ }\)円の弧の長さ\(\small{ \ l \ }\)を弧度法で考えると
\(\small{ \ l=2 \pi r \times \displaystyle \frac{\theta}{2\pi}=r \theta \ }\)
になる。
同じように扇型の面積は
半径\(\small{\times}\)半径\(\small{\times \pi \times \displaystyle \frac{中心角}{360^{\circ}} \ }\)だったから、これを半径\(\small{ \ r \ }\)、中心角\(\small{ \ \theta \ }\)の扇型の面積\(\small{ \ \mathrm{S} \ }\)を弧度法で考えると
\(\small{ \ \mathrm{S}= \pi r^2 \times \displaystyle \frac{\theta}{2\pi}=\displaystyle \frac{1}{2}r^2 \theta \ }\)
になる。
教科書なんかできちんと紹介されてるからここでも書いてるけど、昔覚えた円の円周や面積に\(\small{ \ \displaystyle \frac{中心角}{360^{\circ}} \ }\)をかけることを覚えておけば、わざわざ\(\small{ \ l=r \theta \ }\)や\(\small{ \ \mathrm{S}= \displaystyle \frac{1}{2}r^2 \theta \ }\)を覚えておかなくてもいいからね。
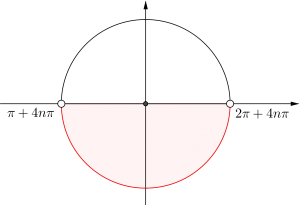
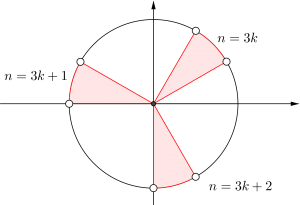
角\(\small{ \ \theta \ }\)の動径が第\(\small{ \ 2 \ }\)象限にあるとき、次の角の動径は第何象限にあるか。
(1)\(\small{ \ 2\theta \ }\)
(2)\(\small{ \ \displaystyle \frac{\theta}{3} \ }\)
\(\small{ \ \theta \ }\)の動径が第\(\small{ \ 2 \ }\)象限にあるとき
\(\small{ \ \displaystyle \frac{\pi}{2}+2n\pi \lt \theta \lt \pi+2n\pi \ }\)
(1)\(\small{ \ \pi+4n\pi \lt 2\theta \lt 2\pi+4n\pi \ }\)
よって第\(\small{ \ 3 \ }\)象限、第\(\small{ \ 4 \ }\)象限
(2)\(\small{ \ \displaystyle \frac{\pi}{6}+\displaystyle \frac{2n}{3}\pi \lt \displaystyle \frac{\theta}{3} \lt \displaystyle \frac{\pi}{3}+\displaystyle \frac{2n}{3}\pi \ }\)
よって第\(\small{ \ 1 \ }\)象限、第\(\small{ \ 2 \ }\)象限、第\(\small{ \ 4 \ }\)象限

Point 三角関数の角の拡張
①一般角\(\small{ \ \theta+2n\pi \ }\)の使い方をマスターしよう

