こんにちは、リンス(@Lins016)です。
今回は連動する点の軌跡の方程式について学習していこう。
動点と求める軌跡の点
今回学習するのは、ある線上を動く点\(\small{ \ \mathrm{Q} \ }\)につられて、ある条件を満たす点\(\small{ \ \mathrm{P} \ }\)の軌跡の問題。この場合、線上を動く点\(\small{ \ \mathrm{Q} \ }\)の座標を\(\small{ \ (a, \ b) \ }\)、求める軌跡の点\(\small{ \ \mathrm{P} \ }\)の座標を\(\small{ \ (x, \ y) \ }\)とおくところから始めよう。
①求める軌跡の点の座標を\(\small{ \ (x, \ y) \ }\)に、線上を動く点を\(\small{ \ (a, \ b) \ }\)に設定。
②\(\small{ \ (a, \ b) \ }\)が線上にあるという式をたてる。
③\(\small{ \ x, \ y \ }\)と\(\small{ \ a, \ b \ }\)の関係式をたてる。
④③の式と②の式から\(\small{ \ a, \ b \ }\)を消去して\(\small{ \ x, \ y \ }\)の式を導く
線上を動く点と求める軌跡の点の座標を異なる文字でおいて、最終的には軌跡の方程式、つまり\(\small{ \ x, \ y \ }\)の関係式を求めるから、動点としておいた\(\small{ \ a, \ b \ }\)を消去していくんだ。
点\(\small{ \ \mathrm{Q} \ }\)が線上にあるという式
まずは与えられた線上に点\(\small{ \ \mathrm{Q} \ }\)があるという式を立てよう。点\(\small{ \ \mathrm{Q} \ }\)の座標\(\small{ \ (a, \ b) \ }\)を線の方程式に代入すればOK。

点\(\small{ \ \mathrm{P} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)の関係式
次に点\(\small{ \ \mathrm{P} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)の関係を式にする。
この関係がなかったら、点\(\small{ \ \mathrm{P} \ }\)は点\(\small{ \ \mathrm{Q} \ }\)につられて動くはずがないから、どういう関係か問題文から読み取ろう。
定期試験によく出題されるパターンは定点\(\small{ \ \mathrm{A} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)の内分点が点\(\small{ \ \mathrm{P} \ }\)や、定点\(\small{ \ \mathrm{A} \ }\)と定点\(\small{ \ \mathrm{B} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)で作られる三角形の重心が点\(\small{ \ \mathrm{P} \ }\)になっていることが多い。

軌跡の方程式を導く
上の二つの式さえたてられたらあとは簡単。
求めたいのは\(\small{ \ x, \ y \ }\)の関係式だから、点\(\small{ \ \mathrm{P} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)の関係式から\(\small{a, \ b}\)をそれぞれ\(\small{ \ x, \ y \ }\)で表そう。
それを点\(\small{ \ \mathrm{Q} \ }\)が線上にあるという式に代入することで\(\small{ \ a, \ b \ }\)が消去されて\(\small{ \ x, \ y \ }\)が残る。これが求める点\(\small{ \ \mathrm{P} \ }\)の軌跡の方程式になるんだ。
このやり方をきちんと覚えて、連動する点の軌跡の方程式をしっかりと解けるようにしておこう。
\(\small{ \ 2 \ }\)定点\(\small{ \ \mathrm{A(6, \ -2)、B(4, \ 5)} \ }\)と円\(\small{ \ (x-2)^2+y^2=9 \ }\)上の動点\(\small{ \ \mathrm{Q} \ }\)に対し、\(\small{ \ \triangle \mathrm{ABQ} \ }\)の重心の軌跡を求めよ。
重心を点\(\small{ \ \mathrm{P} \ }\)、座標を\(\small{ \ (x, \ y) \ }\)、点\(\small{ \ \mathrm{Q} \ }\)の座標を\(\small{ \ (a,b) \ }\)とおく。
\(\small{ \ {(a-2)^2+b^2}=9 \cdots①\ }\)
\(\small{(x,y)=\left(\displaystyle \frac{a+6+4}{3},\frac{b-2+5}{3}\right)\cdots② \ }\)
\(\small{②}\)を変形して、
\(\small{(a, \ b)=(3x-10, \ 3y-2)}\)
これを\(\small{①}\)に代入して
\(\small{(3x-10-2)^2+(3y-3)^2=9}\)
\(\small{9(x-4)^2+9(y-1)^2=9}\)
\(\small{\therefore (x-4)^2+(y-1)^2=1}\)


Point
①求める軌跡の点の座標を\(\small{ \ (x, \ y) \ }\)に、線上を動く点を\(\small{ \ (a, \ b) \ }\)に設定。
②点\(\small{ \ \mathrm{Q} \ }\)が線上にあるという式と点\(\small{ \ \mathrm{P} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)の関係式の2つの式を立てる
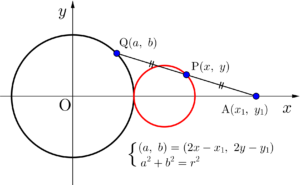
\(\small{ \ xy \ }\)平面上に、原点\(\small{ \ \mathrm{O} \ }\)を中心とする半径\(\small{ \ 1 \ }\)の円\(\small{ \ C \ }\)と、点\(\small{ \ (4, \ 3) \ }\)を中心とする半径\(\small{ \ 1 \ }\)の円\(\small{ \ D \ }\)がある。円\(\small{ \ C \ }\)上に異なる\(\small{ \ 2 \ }\)点\(\small{ \ \mathrm{A} \ }\)、\(\small{ \ \mathrm{B} \ }\)があり、円\(\small{ \ D \ }\)上に点\(\small{ \ \mathrm{P} \ }\)がある。\(\small{ \ 2 \ }\)つの直線\(\small{ \ \mathrm{AP} \ }\)、\(\small{ \ \mathrm{BP} \ }\)は円\(\small{ \ C \ }\)の接線とする。直線\(\small{ \ \mathrm{AB} \ }\)と直線\(\small{ \ \mathrm{OP} \ }\)の交点を\(\small{ \ \mathrm{Q} \ }\)とするとき、以下の問いに答えよ。
(1)点\(\small{ \ \mathrm{P} \ }\)の座標が\(\small{ \ (5, \ 3) \ }\)のとき、直線\(\small{ \ \mathrm{AB} \ }\)の方程式を求めよ。
(2)(1)のとき、点\(\small{ \ \mathrm{Q} \ }\)の座標を求めよ。
(3)点\(\small{ \ \mathrm{P} \ }\)が円\(\small{ \ D \ }\)上を動くとき、点\(\small{ \ \mathrm{Q} \ }\)の軌跡が点\(\small{ \ \left(\displaystyle \frac{1}{6}, \ \displaystyle \frac{1}{8}\right) \ }\)を中心とする半径\(\small{ \ \displaystyle \frac{1}{24} \ }\)の円となることを示せ。
(1)円\(\small{ \ C:x^2+y^2=1 \ }\)
円\(\small{ \ D:(x-4)^2+(y-3)^2=1 \ }\)
点\(\small{ \ \mathrm{A} \ }\)の座標を\(\small{ \ (x_1, \ y_1) \ }\)とおくと、点\(\small{ \ \mathrm{A} \ }\)における接線の方程式は\(\small{ \ x_1x+y_1y=1 \ }\)
これが\(\small{ \ \mathrm{P}(5, \ 3) \ }\)を通るから
\(\small{ \ 5x_1+3y_1=1\cdots① \ }\)
点\(\small{ \ \mathrm{B} \ }\)の座標を\(\small{ \ (x_2, \ y_2) \ }\)とおくと、同様に
\(\small{ \ 5x_2+3y_2=1\cdots② \ }\)
\(\small{ \ ①② \ }\)より直線\(\small{ \ \mathrm{AB} \ }\)の方程式は
\(\small{ \ 5x+3y=1 \ }\)
(2)直線\(\small{ \ \mathrm{OP} \ }\)の方程式は\(\small{ \ y=\displaystyle \frac{3}{5}x \ }\)
これと\(\small{ \ 5x+3y=1 \ }\)の交点を求めると
\(\small{ \ \mathrm{Q}(\displaystyle \frac{5}{34}, \ \displaystyle \frac{3}{34}) \ }\)

(3)円\(\small{ \ D \ }\)上の点\(\small{ \ \mathrm{P} \ }\)の座標を\(\small{ \ (a, \ b) \ }\)とおくと
\(\small{ \ (a-4)^2+(b-3)^2=1\cdots③ \ }\)
直線\(\small{ \ \mathrm{AB} \ }\)の方程式は、(1)と同様にして
\(\small{ \ ax+by=1\cdots④ \ }\)
\(\small{ \ a\neq0 \ }\)より直線\(\small{ \ \mathrm{OP} \ }\)の方程式は\(\small{ \ y=\displaystyle \frac{b}{a}x\cdots⑤ \ }\)
\(\small{④⑤}\)より点\(\small{ \ \mathrm{Q} \ }\)の座標は
\(\small{ \ (x, \ y)=\left(\displaystyle \frac{a}{a^2+b^2}, \ \displaystyle \frac{b}{a^2+b^2}\right) \ }\)
これより\(\small{ \ x^2+y^2=\displaystyle \frac{a^2+b^2}{(a^2+b^2)^2}=\displaystyle \frac{1}{a^2+b^2}\cdots⑥ \ }\)
\(\small{ \ (a, \ b)=\left(\displaystyle \frac{x}{x^2+y^2}, \ \displaystyle \frac{y}{x^2+y^2}\right)\cdots⑦ \ }\)
\(\small{③}\)を展開して\(\small{⑥⑦}\)を代入すると
\(\small{ \ \displaystyle \frac{1}{x^2+y^2}-\displaystyle \frac{8x}{x^2+y^2}-\displaystyle \frac{6y}{x^2+y^2}+24=0 \ }\)
これを整理して
\(\small{ \ x^2+y^2-\displaystyle \frac{1}3{}x-\displaystyle \frac{1}{4}y+\displaystyle \frac{1}{24}=0 \ }\)
\(\small{ \ \left(x-\displaystyle \frac{1}{6}\right)^2+\left(y-\displaystyle \frac{1}{8}\right)^2=\left(\displaystyle \frac{1}{24}\right)^2 \ }\)
よって点\(\small{ \ \mathrm{Q} \ }\)の軌跡は点\(\small{ \ \left(\displaystyle \frac{1}{6}, \ \displaystyle \frac{1}{8}\right) \ }\)を中心とする半径\(\small{ \ \displaystyle \frac{1}{24} \ }\)の円となる

