こんにちは、リンス(@Lins016)です。
今回は空間ベクトルと同一平面上の点について学習していこう。
同一平面上にあるベクトルの条件
空間中の\(\small{ \ 3 \ }\)点を通る平面があるとき、別の\(\small{ \ 4 \ }\)点目がその平面上にあるかっていう条件こそ今回学習するポイントになるからきちんと理解しておこう。
\(\small{ \ 4 \ }\)点\(\small{ \ \mathrm{A, \ B, \ C, \ D} \ }\)が同一平面上にある
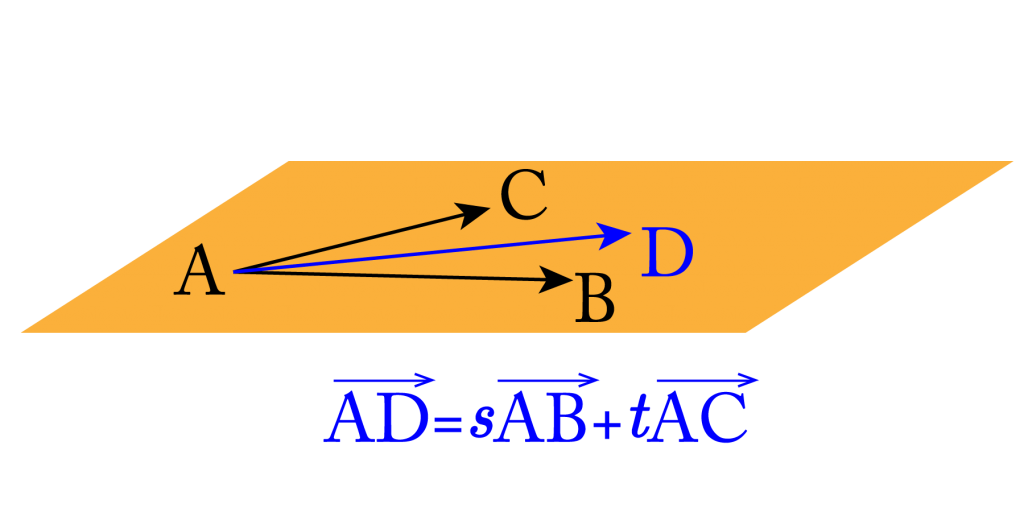
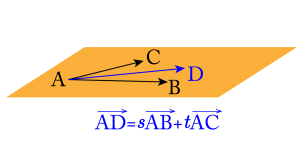
\(\small{ \ \overrightarrow{\mathrm{AD}}=s\overrightarrow{\mathrm{AB}}+t\overrightarrow{\mathrm{AC}} \ }\)を満たす\(\small{ \ s, \ t \ }\)が存在する
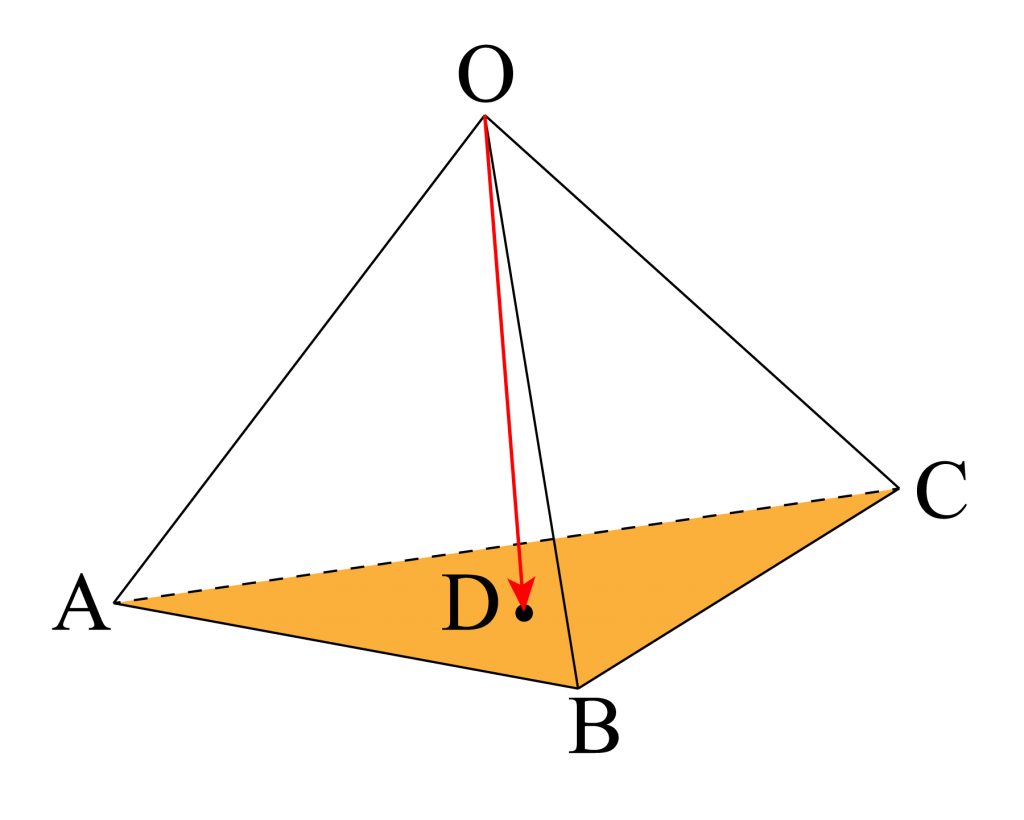
\(\small{ \ \overrightarrow{\mathrm{OD}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)のとき\(\small{ \ 4 \ }\)点\(\small{ \ \mathrm{A, \ B, \ C, \ D} \ }\)が同一平面上にあるなら\(\small{ \ s+t+u=1 \ }\)
4点が同一平面にある
空間中に\(\small{ \ 3 \ }\)点があると、その\(\small{ \ 3 \ }\)点を通る平面って必ず\(\small{ \ 1 \ }\)つ存在する。
つまり\(\small{ \ 3 \ }\)点\(\small{ \ \mathrm{A, \ B, \ C} \ }\)があるとすると\(\small{ \ \overrightarrow{\mathrm{AB}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{AC}} \ }\)はその平面上にあるベクトルってことになるよね。
平面ベクトルの基本で学習したけど、平面ベクトルは平行でない基準のベクトル\(\small{ \ 2 \ }\)つを利用することで、平面上のベクトルを表すことができたよね。
これを利用して空間ベクトルでも空間中の平面の上にある\(\small{ \ 2 \ }\)つのベクトルを利用することでその平面上にあるベクトルを表すことができるんだ。
このことから「\(\small{ \ 4 \ }\)点\(\small{ \ \mathrm{A, \ B, \ C, \ D} \ }\)が同一平面上にある」って言うのは、「\(\small{ \ 3 \ }\)点\(\small{ \ \mathrm{A, \ B, \ C} \ }\)を通る平面上に点\(\small{ \ \mathrm{D} \ }\)がある」って考えればいいんだ。
つまりベクトルを利用すると
\(\small{ \ \overrightarrow{\mathrm{AD}}=s\overrightarrow{\mathrm{AB}}+t\overrightarrow{\mathrm{AC}} \ }\)を満たす\(\small{ \ s, \ t \ }\)が存在するなら\(\small{ \ 4 \ }\)点\(\small{ \ \mathrm{A, \ B, \ C, \ D} \ }\)が同一平面上にあるって言えるんだ。
次の\(\small{ \ 4 \ }\)点が同じ平面上にあるように定数\(\small{ \ a \ }\)の値を求めよ。
\(\small{ \ \mathrm{A}(3, \ 1, \ 2) \ }\)、\(\small{ \ \mathrm{B}(4, \ 2, \ 3) \ }\)、\(\small{ \ \mathrm{C}(5, \ 2, \ 5) \ }\)、\(\small{ \ \mathrm{D}(-2, \ -1, \ a) \ }\)
同一平面上にあるとき
\(\small{ \ \overrightarrow{\mathrm{AD}}=s\overrightarrow{\mathrm{AB}}+t\overrightarrow{\mathrm{AC}} \ }\)が成り立つ
\(\small{\begin{eqnarray} \ (-5, \ -2, \ a-2)&=&s(1, \ 1, \ 1)+t(2, \ 1, \ 3)\\
&=&(s+2t, \ s+t, \ s+3t) \ \end{eqnarray}}\)
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
s+2t=-5\\
s+t=-2\\
s+3t=a-2
\end{array}
\right.
\end{eqnarray}
\ }\)
これを解いて\(\small{ \ s=1, \ t=-3, \ a=-6 \ }\)
係数の和が1になる
「\(\small{ \ 4 \ }\)点\(\small{ \ \mathrm{A, \ B, \ C, \ D} \ }\)が同一平面上にある」って言うのは、「\(\small{ \ 3 \ }\)点\(\small{ \ \mathrm{A, \ B, \ C} \ }\)を通る平面上に点\(\small{ \ \mathrm{D} \ }\)がある」って考えれば良かったから上では\(\small{ \ \overrightarrow{\mathrm{AD}}=s\overrightarrow{\mathrm{AB}}+t\overrightarrow{\mathrm{AC}} \ }\)が言えれば\(\small{ \ 4 \ }\)点\(\small{ \ \mathrm{A, \ B, \ C, \ D} \ }\)ってしたけど、基準のベクトルを\(\small{ \ \mathrm{C} \ }\)から始まるベクトルにしても問題ないんだ。
つまり\(\small{ \ \overrightarrow{\mathrm{CD}}=s\overrightarrow{\mathrm{CA}}+t\overrightarrow{\mathrm{CB}} \ }\)ってことね。
これを\(\small{ \ \mathrm{O} \ }\)から始まるベクトルに変えてみよう。
\(\small{ \ \overrightarrow{\mathrm{OD}}-\overrightarrow{\mathrm{OC}}=s\left(\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OC}}\right)+t\left(\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}\right) \ }\)
\(\small{ \ \overrightarrow{\mathrm{OD}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+(1-s-t)\overrightarrow{\mathrm{OC}} \ }\)
\(\small{ \ 1-s-t=u \ }\)ってすると
\(\small{ \ \overrightarrow{\mathrm{OD}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)で
\(\small{ \ s+t+u=1 \ }\)になるんだ。
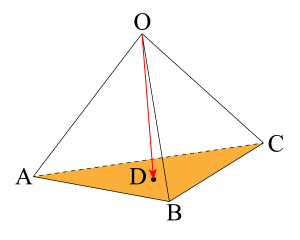
つまり\(\small{ \ \overrightarrow{\mathrm{OD}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)のとき、\(\small{ \ s+t+u=1 \ }\)なら\(\small{ \ 4 \ }\)点\(\small{ \ \mathrm{A, \ B, \ C, \ D} \ }\)が同一平面上にあるって言えるんだ。
四面体\(\small{ \ \mathrm{ABCD} \ }\)がある。\(\small{ \ \mathrm{AB} \ }\)を\(\small{ \ 1:2 \ }\)に、\(\small{ \ \mathrm{AC} \ }\)を\(\small{ \ 2:1 \ }\)に、\(\small{ \ \mathrm{AD} \ }\)を\(\small{ \ 1:1 \ }\)に内分する点をそれぞれ\(\small{ \ \mathrm{L, \ M, \ N} \ }\)とする。
\(\small{ \ \triangle\mathrm{BCD} \ }\)の重心\(\small{ \ \mathrm{G} \ }\)と\(\small{ \ \mathrm{A} \ }\)を結ぶ線分が平面\(\small{ \ \mathrm{LMN} \ }\)と交わる点を\(\small{ \ \mathrm{P} \ }\)とする。\(\small{ \ \overrightarrow{\mathrm{AP}} \ }\)を\(\small{ \ \overrightarrow{\mathrm{AB}} \ }\),\(\small{ \ \overrightarrow{\mathrm{AC}} \ }\),\(\small{ \ \overrightarrow{\mathrm{AD}} \ }\)を用いて表せ。
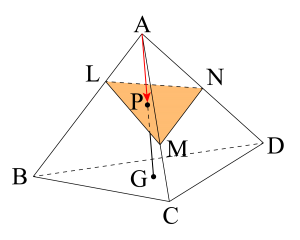
\(\small{ \ \overrightarrow{\mathrm{AL}}=\displaystyle\frac{1}{3}\overrightarrow{\mathrm{AB}} \ }\)
\(\small{ \ \overrightarrow{\mathrm{AM}}=\displaystyle\frac{2}{3}\overrightarrow{\mathrm{AC}} \ }\)
\(\small{ \ \overrightarrow{\mathrm{AN}}=\displaystyle\frac{1}{2}\overrightarrow{\mathrm{AD}} \ }\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AG}}&=&\displaystyle\frac{\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{AD}}}{3}\\
&=&\overrightarrow{\mathrm{AL}}+\displaystyle\frac{1}{2}\overrightarrow{\mathrm{AM}}+\displaystyle\frac{2}{3}\overrightarrow{\mathrm{AN}} \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AP}}&=&k\overrightarrow{\mathrm{AG}}\\
&=&k\overrightarrow{\mathrm{AL}}+\displaystyle\frac{1}{2}k\overrightarrow{\mathrm{AM}}+\displaystyle\frac{2}{3}k\overrightarrow{\mathrm{AN}} \ \end{eqnarray}}\)
\(\small{ \ k+\displaystyle\frac{1}{2}k+\displaystyle\frac{2}{3}k=1 \ }\)
\(\small{ \ k=\displaystyle\frac{6}{13} \ }\)
\(\small{ \ \overrightarrow{\mathrm{AP}}=\displaystyle\frac{6}{13}\overrightarrow{\mathrm{AL}}+\displaystyle\frac{3}{13}\overrightarrow{\mathrm{AM}}+\displaystyle\frac{4}{13}\overrightarrow{\mathrm{AN}} \ }\)
\(\small{ \ \therefore \overrightarrow{\mathrm{AP}}=\displaystyle\frac{2}{13}\overrightarrow{\mathrm{AB}}+\displaystyle\frac{2}{13}\overrightarrow{\mathrm{AC}}+\displaystyle\frac{2}{13}\overrightarrow{\mathrm{AC}} \ }\)
\(\small{ \ \overrightarrow{\mathrm{AL}}=\displaystyle\frac{1}{3}\overrightarrow{\mathrm{AB}} \ }\)
\(\small{ \ \overrightarrow{\mathrm{AM}}=\displaystyle\frac{2}{3}\overrightarrow{\mathrm{AC}} \ }\)
\(\small{ \ \overrightarrow{\mathrm{AN}}=\displaystyle\frac{1}{2}\overrightarrow{\mathrm{AD}} \ }\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AG}}&=&\displaystyle\frac{\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{AD}}}{3}\\
&=&\displaystyle\frac{3\overrightarrow{\mathrm{AL}}+\displaystyle\frac{3}{2}\overrightarrow{\mathrm{AM}}+2\overrightarrow{\mathrm{AN}}}{3}\\
&=&\displaystyle\frac{3+\displaystyle\frac{3}{2}+2}{3}\cdot\displaystyle\frac{3\overrightarrow{\mathrm{AL}}+\displaystyle\frac{3}{2}\overrightarrow{\mathrm{AM}}+2\overrightarrow{\mathrm{AN}}}{3+\displaystyle\frac{3}{2}+2}\\
&=&\displaystyle\frac{13}{6}\cdot\displaystyle\frac{6\overrightarrow{\mathrm{AL}}+3\overrightarrow{\mathrm{AM}}+4\overrightarrow{\mathrm{AN}}}{13} \ \end{eqnarray}}\)
\(\small{ \ \overrightarrow{\mathrm{AP}}=\displaystyle\frac{6\overrightarrow{\mathrm{AL}}+3\overrightarrow{\mathrm{AM}}+4\overrightarrow{\mathrm{AN}}}{13} \ }\)
\(\small{ \ \therefore \overrightarrow{\mathrm{AP}}=\displaystyle\frac{2}{13}\overrightarrow{\mathrm{AB}}+\displaystyle\frac{2}{13}\overrightarrow{\mathrm{AC}}+\displaystyle\frac{2}{13}\overrightarrow{\mathrm{AC}} \ }\)

Point 空間ベクトルと同一平面上の点
①\(\small{ \ \overrightarrow{\mathrm{AD}}=s\overrightarrow{\mathrm{AB}}+t\overrightarrow{\mathrm{AC}} \ }\)を満たす\(\small{ \ s, \ t \ }\)が存在するなら\(\small{ \ 4 \ }\)点\(\small{ \ \mathrm{A, \ B, \ C, \ D} \ }\)が同一平面上にある
②\(\small{ \ \overrightarrow{\mathrm{OD}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)のとき\(\small{ \ s+t+u=1 \ }\)なら\(\small{ \ 4 \ }\)点\(\small{ \ \mathrm{A, \ B, \ C, \ D} \ }\)が同一平面上にある
\(\small{ \ \def\cenBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ }}\def\cenbox#1{\bbox[4px, border:1px solid gray]{\ #1\ }} \ }\)空間に\(\small{ \ 4 \ }\)点\(\small{ \ \mathrm{A}(2, \ 1, \ 3) \ }\)、\(\small{ \ \mathrm{B}(-3, \ 1, \ 5) \ }\)、\(\small{ \ \mathrm{C}(4, \ 2, \ 1) \ }\)、\(\small{ \ \mathrm{D}(8, \ 5, \ 2x-5) \ }\)があり、この\(\small{ \ 4 \ }\)点は同一平面上にある。\(\small{ \ 2 \ }\)直線\(\small{ \ \mathrm{BC} \ }\)、\(\small{ \ \mathrm{AD} \ }\)の交点を\(\small{ \ \mathrm{E} \ }\)とおく。このとき
(i)\(\small{ \ x=\displaystyle\frac{\cenbox{アイ}}{\cenbox{ウ}} \ }\)である
(ii)\(\small{ \ \triangle\mathrm{ACE} \ }\)の面積は\(\small{ \ \displaystyle\frac{ \cenbox{エ}\sqrt{\cenbox{オカ}}}{\cenbox{キク}} \ }\)である。
(i)
\(\small{ \ 4 \ }\)点\(\small{ \ \mathrm{A, \ B, \ C, \ D} \ }\)が同じ平面上にあるとき、
\(\small{ \ \overrightarrow{\mathrm{AD}}=s\overrightarrow{\mathrm{AB}}+t\overrightarrow{\mathrm{AC}} \ }\)(\(\small{ \ s, \ t \ }\))は実数)で表されるので
\(\small{\begin{eqnarray} \ (6, \ 4, \ 2x-8)&=&s(-5, \ 0, \ -8)+t(2, \ 1, \ -2)\\
&=&(-5s+2t, \ t, \ -8s-2t) \ \end{eqnarray}}\)
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
-5s+2t=6\\
t=4\\
-8s-2t=2x-8
\end{array}
\right.
\end{eqnarray}
\ }\)
これを解いて\(\small{ \ s=\displaystyle\frac{2}{5}, \ t=4, \ x=-\displaystyle\frac{8}{5} \ }\)
(ii)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AD}}&=&\displaystyle\frac{2}{5}\overrightarrow{\mathrm{AB}}+4\overrightarrow{\mathrm{AC}}\\
&=&\displaystyle\frac{22}{5}\cdot\displaystyle\frac{\overrightarrow{\mathrm{AB}}+10\overrightarrow{\mathrm{AC}}}{11}\\
&=&\displaystyle\frac{22}{5}\overrightarrow{\mathrm{AE}} \ \end{eqnarray}}\)
\(\small{ \ \mathrm{E} \ }\)は線分\(\small{ \ \mathrm{BC} \ }\)を\(\small{ \ 10:1 \ }\)に内分する点で
\(\small{ \ \triangle\mathrm{ACD}=\displaystyle\frac{1}{11}\triangle\mathrm{ABC} \ }\)

\(\small{\begin{eqnarray} \ \triangle\mathrm{ABC}&=&\displaystyle\frac{1}{2}\sqrt{\vert\overrightarrow{\mathrm{AB}}\vert^2\vert\overrightarrow{\mathrm{AC}}\vert^2-\left(\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}\right)^2}\\
&=&\displaystyle\frac{1}{2}\sqrt{89\cdot9-6^2}\\
&=&\displaystyle\frac{3\sqrt{85}}{2} \ \end{eqnarray}}\)
\(\small{ \ \therefore \triangle\mathrm{ABC}=\displaystyle\frac{3\sqrt{85}}{22} \ }\)

