こんにちは、リンス(@Lins016)です。
今回は空間の位置ベクトルと内分点・外分点のベクトルについて学習していこう。
空間の位置ベクトルと内分点・外分点
空間ベクトルでも位置ベクトルってよく出題されるから、しっかりと押さえておきたい。
\(\small{ \ 2 \ }\)点の内分や外分を求めたりする場合、平面ベクトルの内分や外分の考え方と同じだから、内分・外分の公式を使って解こう。
まずは一度前の平面ベクトルの記事を読んでから進めていこう。
\(\small{ \ \mathrm{P}(\overrightarrow{p}) \ }\)、\(\small{ \ \mathrm{Q}(\overrightarrow{q}) \ }\)のとき
\(\small{ \ \overrightarrow{\mathrm{PQ}}=\overrightarrow{q}-\overrightarrow{p} \ }\)
内分
\(\small{ \ \overrightarrow{r}=\displaystyle\frac{n\overrightarrow{p}+m\overrightarrow{q}}{m+n} \ }\)
外分
\(\small{ \ \overrightarrow{s}=\displaystyle\frac{-n\overrightarrow{p}+m\overrightarrow{q}}{m-n} \ }\)
位置ベクトルの考え方
平面ベクトルでも学習したけど、空間ベクトルの場合も同じで、位置ベクトルって原点\(\small{ \ \mathrm{O} \ }\)と点を結んだベクトルのことで、その点が原点に対してどんな位置にあるかをベクトルで表したものになるんだ。
点\(\small{ \ \mathrm{A} \ }\)の位置ベクトルを\(\small{ \ \mathrm{A}(\overrightarrow{a}) \ }\)のように書く。
これは原点\(\small{ \ \mathrm{O} \ }\)が始点で点\(\small{ \ \mathrm{A} \ }\)が終点のベクトル\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)を\(\small{ \ \overrightarrow{a} \ }\)と表していて、平面の位置ベクトルの考え方と同じだからね。
平面だと「\(\small{ \ \mathrm{A}(\overrightarrow{a}) \ }\)、\(\small{ \ \mathrm{B}(\overrightarrow{b}) \ }\)のとき」って書いてあったのが、空間だと「\(\small{ \ \mathrm{A}(\overrightarrow{a}) \ }\)、\(\small{ \ \mathrm{B}(\overrightarrow{b}) \ }\)、\(\small{ \ \mathrm{C}(\overrightarrow{c}) \ }\)のとき」って基準のベクトルが\(\small{ \ 3 \ }\)つに増えることになるからね。
\(\small{ \ \mathrm{A, \ B, \ C} \ }\)はの3点は一つの平面上にあるけど、この平面上にない、どこかに原点\(\small{ \ \mathrm{O} \ }\)があると、空間ベクトルの問題になるからね。
内分点と外分点と空間ベクトル
空間ベクトルは\(\small{ \ 3 \ }\)つの基準のベクトルが必要だってことは、これまでも散々伝えてきたよね。
だから内分点や外分点を表すベクトルも\(\small{ \ 3 \ }\)つの基準のベクトルを利用して表すことになるんだ。
だけど、そもそも内分点を表すベクトルって\(\small{ \ 2 \ }\)点の内分点だよね?
例えば\(\small{ \ \mathrm{P}(\overrightarrow{p}) \ }\)と\(\small{ \ \mathrm{Q}(\overrightarrow{q}) \ }\)を\(\small{ \ m:n \ }\)に内分する\(\small{ \ \mathrm{R}(\overrightarrow{r}) \ }\)って言われた場合、図を書くと\(\small{ \ \overrightarrow{p} \ }\)と\(\small{ \ \overrightarrow{q} \ }\)が作る平面上に\(\small{ \ \overrightarrow{r} \ }\)もあるのがわかるよね。
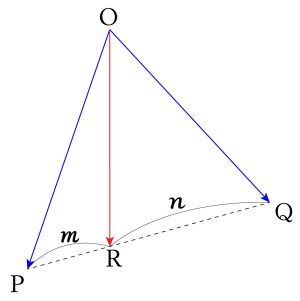
つまりここだけみると空間ベクトルじゃなくて平面ベクトルになるんだ。つまり平面ベクトルの内分点の求め方と同じってことになるよね。
だから空間ベクトルの内分や外分も平面ベクトルと同じように扱ってしまえばいいんだ。そんなに難しいことじゃないよね。
ただ、基準のベクトルを\(\small{ \ \overrightarrow{a}, \ \overrightarrow{b}, \ \overrightarrow{c} \ }\)とすると\(\small{ \ \overrightarrow{p} \ }\)や\(\small{ \ \overrightarrow{q} \ }\)は\(\small{ \ s\overrightarrow{a}+t\overrightarrow{b}+u\overrightarrow{c} \ }\)の形で表されるベクトルになるから、結果として\(\small{ \ \overrightarrow{a}, \ \overrightarrow{b}, \ \overrightarrow{c} \ }\)を利用した空間ベクトルになるんだ。
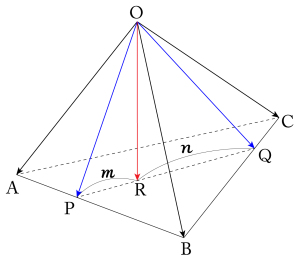
四面体\(\small{ \ \mathrm{ABCD} \ }\)の辺\(\small{ \ \mathrm{AB, \ BC, \ CD} \ }\)をそれぞれ\(\small{ \ 5:3, \ 3:1, \ 7:1 \ }\)に内分する点を\(\small{ \ \mathrm{P, \ Q, \ R} \ }\)とする。\(\small{ \ \triangle\mathrm{BCD}, \ \triangle\mathrm{PQR} \ }\)の重心をそれぞれ\(\small{ \ \mathrm{G, \ H} \ }\)とするとき、\(\small{ \ \mathrm{A, \ H, \ G} \ }\)は一直線上にあることを示せ。
\(\small{ \ \overrightarrow{\mathrm{AP}}=\displaystyle\frac{5}{8}\overrightarrow{\mathrm{AB}} \ }\)
\(\small{ \ \overrightarrow{\mathrm{AQ}}=\displaystyle\frac{1}{4}\overrightarrow{\mathrm{AB}}+\displaystyle\frac{3}{4}\overrightarrow{\mathrm{AC}} \ }\)
\(\small{ \ \overrightarrow{\mathrm{AR}}=\displaystyle\frac{1}{8}\overrightarrow{\mathrm{AC}}+\displaystyle\frac{7}{8}\overrightarrow{\mathrm{AD}} \ }\)
\(\small{ \ \overrightarrow{\mathrm{AG}}=\displaystyle\frac{1}{3}\left(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{AD}}\right) \ }\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AH}}&=&\displaystyle\frac{1}{3}\left(\overrightarrow{\mathrm{AP}}+\overrightarrow{\mathrm{AQ}}+\overrightarrow{\mathrm{AR}}\right)\\
&=&\displaystyle\frac{1}{3}\left(\displaystyle\frac{7}{8}\overrightarrow{\mathrm{AB}}+\displaystyle\frac{7}{8}\overrightarrow{\mathrm{AC}}+\displaystyle\frac{7}{8}\overrightarrow{\mathrm{AD}}\right)\\
&=&\displaystyle\frac{7}{8}\overrightarrow{\mathrm{AG}} \ \end{eqnarray}}\)

また、内分の公式を利用して一つ一つ丁寧にベクトルを求めていこう。
\(\small{ \ \overrightarrow{\mathrm{AH}}=\displaystyle\frac{7}{8}\overrightarrow{\mathrm{AG}} \ }\)から\(\small{ \ \mathrm{AH}:\mathrm{HG}=7:1 \ }\)になるからね。
Point 空間の位置ベクトルと内分点・外分点のベクトル
①位置ベクトルとはある点を基準にしたベクトルのこと
②内分や外分のベクトルは平面ベクトルのときの公式と同じ
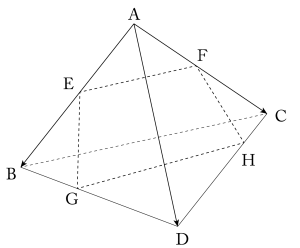
\(\small{ \ 1 \ }\)辺の長さが\(\small{ \ 1 \ }\)の正四面体\(\small{ \ \mathrm{ABCD} \ }\)に対し、辺\(\small{ \ \mathrm{AB} \ }\)の中点を\(\small{ \ \mathrm{E} \ }\)、辺\(\small{ \ \mathrm{AC} \ }\)の中点を\(\small{ \ \mathrm{F} \ }\)、辺\(\small{ \ \mathrm{BD} \ }\)を\(\small{ \ t:(1-t) \ }\)の比に内分する点を\(\small{ \ \mathrm{G} \ }\)、辺\(\small{ \ \mathrm{CD} \ }\)を\(\small{ \ u:(1-u) \ }\)の比に内分する点を\(\small{ \ \mathrm{H} \ }\)とする。ただし\(\small{ \ 0\lt t \lt1 \ }\)、\(\small{ \ 0\lt u \lt1 \ }\)とする
(1)\(\small{ \ 4 \ }\)点\(\small{ \ \mathrm{E, \ F, \ G, \ H} \ }\)が同一平面上にあるならば、\(\small{ \ t=u \ }\)が成り立つことを示せ。
(2)\(\small{ \ t=u \ }\)のとき、\(\small{ \ \mathrm{EF}^2+\mathrm{FH}^2+\mathrm{HG}^2+\mathrm{GE}^2 \ }\)の値の範囲を求めよ。
\(\small{ \ \overrightarrow{\mathrm{AF}}= \displaystyle\frac{1}{2 } \overrightarrow{\mathrm{AC}} \ }\)
\(\small{ \ \overrightarrow{\mathrm{AG}}=(1-t) \overrightarrow{\mathrm{AB}}+t \overrightarrow{\mathrm{AD}} \ }\)
\(\small{ \ \overrightarrow{\mathrm{AH}}=(1-u) \overrightarrow{\mathrm{AC}}+u\overrightarrow{\mathrm{AD}} \ }\)\(\small{ \ 4 \ }\)点\(\small{ \ \mathrm{E, \ F, \ G, \ H} \ }\)が同一平面上にあるとき
\(\small{ \ \overrightarrow{\mathrm{EH}}=\alpha \overrightarrow{\mathrm{EF}}+\beta \overrightarrow{\mathrm{EG}}\cdots① \ }\)
を満たす \(\small{ \ \alpha, \ \beta \ }\)が存在する。
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{EH}}&=& \overrightarrow{\mathrm{AH}}- \overrightarrow{\mathrm{AE}}\\
&=&(1-u) \overrightarrow{\mathrm{AC}}+u\overrightarrow{\mathrm{AD}}-\displaystyle\frac{1}{2 } \overrightarrow{\mathrm{AB}} \ \end{eqnarray}}\)
\(\small{ \ \overrightarrow{\mathrm{EF}}= \displaystyle\frac{1}{2 }\left(\overrightarrow{\mathrm{AC}}- \overrightarrow{\mathrm{AB}}\right) \ }\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{EG}}&=& \overrightarrow{\mathrm{AG}}- \overrightarrow{\mathrm{AE}}\\
&=&(1-t) \overrightarrow{\mathrm{AB}}+t\overrightarrow{\mathrm{AD}}-\displaystyle\frac{1}{2 } \overrightarrow{\mathrm{AB}}\\
&=& \left( \displaystyle\frac{1}{2 }-t\right)\overrightarrow{\mathrm{AB}}+t \overrightarrow{\mathrm{AD}} \ \end{eqnarray}}\)
これを\(\small{ \ ① \ }\)に代入して
=\alpha\cdot \displaystyle\frac{1}{2}\left(\overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{AB}}\right)+\beta \cdot\left\{ \left( \displaystyle\frac{1}{2}-t\right)\overrightarrow{\mathrm{AB}}+t \overrightarrow{\mathrm{AD}} \right\}\\
=\left\{-\displaystyle\frac{\alpha}{2}+\beta\left(\displaystyle\frac{1}{2}-t\right)\right\}\overrightarrow{\mathrm{AB}}+\displaystyle\frac{\alpha}{2}\overrightarrow{\mathrm{AC}}+\beta t \overrightarrow{\mathrm{AD}} \ }\)
\(\small{ \ \overrightarrow{\mathrm{AB}}, \ \overrightarrow{\mathrm{AC}}, \ \overrightarrow{\mathrm{AD}} \ }\)は\(\small{ \ \overrightarrow{0} \ }\)でなく、どの\(\small{ \ 2 \ }\)つも平行でないから、各ベクトルの係数を比較して
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
-\displaystyle\frac{1}{2}=-\displaystyle\frac{\alpha}{2}+\beta\left(\displaystyle\frac{1}{2}-t\right)\\
1-u=\displaystyle\frac{\alpha}{2}\\
u=\beta t
\end{array}
\right.
\end{eqnarray} \ }\)
この式をそれぞれ加えると
\(\small{ \ \displaystyle\frac{1}{2}=\displaystyle\frac{\beta}{2} \ }\)よって\(\small{ \ \beta=1 \ }\)
これより\(\small{ \ t=u \ }\)
(2)\(\small{ \ t=u \ }\)のとき
\(\small{ \ \mathrm{BG=CH=}u \ }\)、\(\small{ \ \mathrm{HG}=1-u \ }\)
さらに\(\small{ \ \mathrm{EF}=\displaystyle\frac{1}{2}\mathrm{BC}=\displaystyle\frac{1}{2} \ }\)
\(\small{ \ \mathrm{BE}=\mathrm{CF}=\displaystyle\frac{1}{2} \ }\)
\(\small{ \ \triangle\mathrm{CFH} \ }\)は\(\small{ \ \angle\mathrm{FCH}=60^{\circ} \ }\)だから余弦定理を用いて
&=&\left(\displaystyle\frac{1}{2}\right)^2+u^2-2\cdot\displaystyle\frac{1}{2}\cdot u\cdot\displaystyle\frac{1}{2}\\
&=&u^2-\displaystyle\frac{1}{2}u+\displaystyle\frac{1}{4} \ \end{eqnarray}}\)
同様に\(\small{ \ \mathrm{GE}^2=u^2-\displaystyle\frac{1}{2}u+\displaystyle\frac{1}{4} \ }\)
したがって
\(\small{ \ \mathrm{EF}^2+\mathrm{FH}^2+\mathrm{HG}^2+\mathrm{GE}^2 \ }\)
\(\small{ \ =3u^2-3u+\displaystyle\frac{7}{4} \ }\)
\(\small{ \ =3\left(u-\displaystyle\frac{1}{2}\right)^2+1 \ }\)
\(\small{ \ 0\lt u \lt 1 \ }\)より
\(\small{ \ 1\leqq \mathrm{EF}^2+\mathrm{FH}^2+\mathrm{HG}^2+\mathrm{GE}^2\lt\displaystyle\frac{7}{4} \ }\)

