円に内接する四角形

こんにちは、リンス(@Lins016)です。
今回は円に内接する四角形について学習していこう。

円に内接する四角形の問題の解き方

ただの四角形じゃなくて、円に内接するってのが一番のポイントで、これは四角形の対角の和が$\small{ \ 180^{\circ} \ }$になるってことだからね。

正弦や余弦の補角($\small{ \ 180^{\circ}-\theta \ }$)の式をうまく利用して問題を解いていこう。

円に内接する四角形

・円に内接する四角形の性質
対角の和が$\small{ \ 180^{\circ}　\ }$
$\small{ \ \sin(180^{\circ}-\theta)=\sin\theta \ }$
$\small{ \ \cos(180^{\circ}-\theta)=-\cos \theta \ }$

円に内接する四角形の対角の和は180°

円に内接する四角形といったらまずは対角の和が$\small{ \ 180^{\circ} \ }$っていうことが一番大切なんだ。
なぜ対角の和が$\small{ \ 180^{\circ} \ }$になるかっていうと、円周角と中心角の関係って覚えてるかな？
弧に対する中心角は円周角の$\small{ \ 2 \ }$倍になるんだ。

図を見れば明らかだけど弧$\small{ \ \mathrm{AC} \ }$に対する円周角を点$\small{ \ \mathrm{B} \ }$と点$\small{ \ \mathrm{D} \ }$にそれぞれとって$\small{ \ \alpha \ }$と$\small{ \ \beta \ }$とすると、中心角は円周角の$\small{ \ 2 \ }$倍だから$\small{ \ 2\alpha \ }$と$\small{ \ 2\beta \ }$になる。

これが$\small{ \ 2\alpha+2\beta360{\circ} \ }$になるから、$\small{ \ \alpha+\beta=180^{\circ} \ }$になるよね。

だから円に内接する四角形の対角の和は$\small{ \ 180^{\circ}\ }$になるんだ。

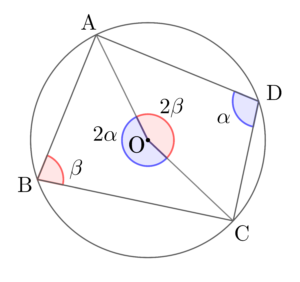
円に内接する四角形は対角線で分割して二つの三角形を作り出す

まずは対角線を引いて二つの三角形を作り出そう。正弦定理や余弦定理は三角形の公式だから対角線で四角形を二分割して三角形を二つの作って、この二つの三角形に公式を利用して値を求めるんだ。

補角の三角比と対角線

円に内接する四角形の対角の和が$\small{ \ 180^{\circ} \ }$になるから補角の三角比の関係を余弦定理や正弦定理に利用しよう。分割した二つの三角形は一辺が共通してることと、補角の三角比の関係が使えることを覚えておこう。
$\small{ \ \sin(180^{\circ}-\theta)=\sin\theta \ }$
$\small{ \ \cos(180^{\circ}-\theta)=-\cos \theta \ }$
すると、それぞれの三角形に余弦定理を利用することで、対角線と余弦を求めることが出来るからね。

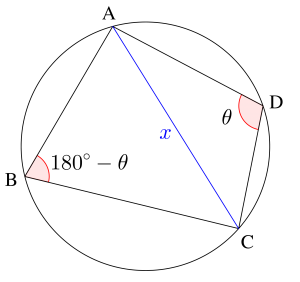
四角形$\small{ \ \mathrm{ABCD} \ }$の各辺の長さが与えられているとき$\small{ \ \mathrm{AB}=a \ }$、$\small{ \ \mathrm{BC}=b \ }$、$\small{ \ \mathrm{CD}=c \ }$、$\small{ \ \mathrm{DA}=d \ }$、$\small{ \ \mathrm{AC}=x \ }$とすると
$\small{\begin{eqnarray} \ x^2&=&a^2+b^2-2ab\cos(180^{\circ}- \theta)\\[4pt] &=&c^2+d^2-2cd\cos \theta \ \end{eqnarray}}$
が言えるから$\small{ \ \cos(180^{\circ}- \theta)=- \cos \theta \ }$を利用すれば、$\small{ \ \cos \theta \ }$を求めることが出来るから対角線の $\small{ \ x \ }$も求めることができるよね。

分割した三角形の外接円が四角形の外接円

円に内接しているのは四角形だけじゃなくて、分割した二つの三角形もそれぞれ円に内接してるから、分割した三角形の正弦定理から円の半径を求めよう。

そのためには対角線の長さを求める必要が出てくるからね。余弦定理で対角線の長さと余弦を求めたら、$\small{ \ \sin^2\theta+\cos^2\theta=1 \ }$から正弦を求めて、正弦定理を利用しよう。

方べきの定理とトレミーの定理

定期試験ではあまり利用することはないと思うけど、入試問題だったら、円に内接する四角形の性質として、方べきの定理やトレミーの定理を使うこともあるから、きちんとおさえておこう。

問題解答

円に内接する四角形$\small{ \ \mathrm{ABCD} \ }$において
$\small{ \ \mathrm{AB}=3, \ \mathrm{BC}=1, \ \mathrm{CD}=3, \ \mathrm{DA}=4 \ }$のとき次の値を求めよ。
(1)$\small{ \ \angle \mathrm{A} \ }$の大きさ
(2)対角線$\small{ \ \mathrm{BD} \ }$の長さ
(3)四角形$\small{ \ \mathrm{ABCD} \ }$の面積
(4)円の半径

(1)$\small{ \ \triangle\mathrm{ABD} \ }$に余弦定理を利用すると
$\small{\begin{eqnarray} \ \mathrm{BD}^2&=&3^2+4^2-2\cdot3\cdot4\cos\mathrm{A}\\ &=&25-24\cos\mathrm{A}\cdots① \ \end{eqnarray}}$
$\small{ \ \triangle\mathrm{BCD} \ }$に余弦定理を利用すると
$\small{ \ \begin{eqnarray}\mathrm{BD}^2&=&1^2+3^2-2\cdot1\cdot3\cos\mathrm{C}\\ &=&10-6\cos(180^{\circ}-\mathrm{A}) \\ \ \ &&(\because \mathrm{A}+\mathrm{C}=180^{\circ})\\ &=&10+6\cos\mathrm{A}\cdots② \ \end{eqnarray}}$
$\small{ \ ①, \ ② \ }$より
$\small{ \ 25-24\cos\mathrm{A}=10+6\cos\mathrm{A} \ }$
$\small{ \ \therefore \cos\mathrm{A}=\displaystyle\frac{1}{2} \ }$
したがって$\small{ \ \mathrm{A}=60^{\circ} \ }$

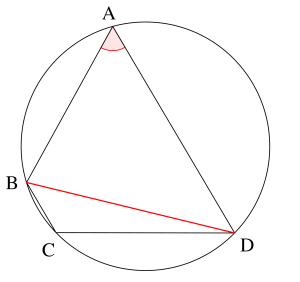
(2)$\small{ \ ① \ }$より
$\small{ \ \mathrm{BD}^2=25-24\cos\mathrm{A}=13 \ }$
よって$\small{ \ \mathrm{BD}=\sqrt{13} \ }$

(3)四角形$\small{ \ \mathrm{ABCD} \ }$の面積を$\small{ \ \mathrm{S} \ }$とすると
$\small{\begin{eqnarray} \ \mathrm{S}&=&\triangle\mathrm{ABD}+\triangle\mathrm{BCD}\\[8pt] &=&\displaystyle\frac{1}{2}\cdot3\cdot4\sin60^{\circ}+\displaystyle\frac{1}{2}\cdot1\cdot3\sin120^{\circ}\\[8pt] &=&\displaystyle\frac{15\sqrt{3}}{4} \ \end{eqnarray}}$

(4)正弦定理より
$\small{ \ \displaystyle \frac{\mathrm{BD}}{\sin \mathrm{A}}=2R \ }$より
$\small{ \ R= \displaystyle \frac{\sqrt{39}}{3} \ }$

今回のこの例題の解き方は定番中の定番の解き方になるから、円に内接する四角形の問題として、丸暗記しててもいいからね。

Point　円に内接する四角形

①円に内接する四角形は対角線で二つの三角形に分割しよう
②二つの三角形に余弦定理を適用しよう