こんにちは、リンス(@Lins016)です。
今回は二次関数の最大・最小の基本について学習していこう。
二次関数の最大値・最小値問題の基本
二次関数の最大最小問題には場合分けの問題など、幾つかのパターンに分けられるけど、まずは基本となる定数が入っていない二次関数の最大・最小について学習していこう。
\(\small{ \ y=a(x-p)^2+q \ }\)
定義域がない場合
\(\small{ \ a\gt0 \ }\)なら最小値\(\small{ \ q \ (x=p \ }\)のとき)
\(\small{ \ a\lt0 \ }\)なら最小値\(\small{ \ q \ (x=p \ }\)のとき)
平方完成とグラフの頂点
まずは基本となる最大値と最小値について学習しよう。
最大値・最小値を求めるためには、二次関数を平方完成してグラフの頂点を求めよう。
定義域が存在しない場合、下に凸のグラフは頂点の\(\normalsize{ \ y \ }\)座標が最小値になって、グラフはそこからずっとに上がっていくから最大値は存在しない。だから最大値は「なし」になるからね。
上に凸のグラフの場合はこの逆で、頂点の\(\normalsize{ \ y \ }\)座標が最大値になって、グラフはそこからずっとに下がっていくから最小値は存在しない。だから最小値は「なし」になるからね。
軸と定義域の位置関係
定義域が存在する場合にはグラフの軸が定義域に対してどの位置にあるかによって最大値や最小値をとる\(\normalsize{ \ x \ }\)の値が変わるからグラフを書いて、軸と定義域の位置関係から判断していこう。
定義域が\(\small{ \ \alpha \leqq x \leqq \beta \ }\)のとき、\(\small{ \ f(x) \ }\)の最大値や最小値は単純に\(\small{ \ f(\alpha) \ }\)、\(\small{f(\beta) \ }\)になるわけじゃないから、きちんと定義域と軸の位置を調べて最大値や最小値をとるときの\(\small{ \ x \ }\)の値を求めよう。
①定義域が軸の左側にある場合
最大値\(\small{ \ f(\alpha) \ }\)、最小値\(\small{ \ f(\beta) \ }\)
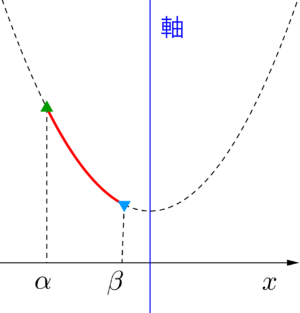
②定義域の内に軸があり、軸が定義域中央より左側にある場合
最大値\(\small{ \ f(\alpha) \ }\)、最小値\(\small{ \ f(軸) \ }\)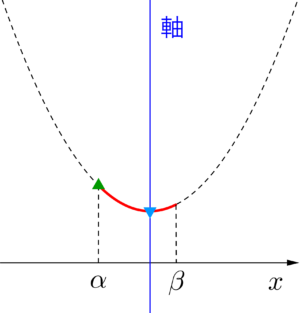
③定義域の内に軸があり、軸が定義域中央より右側にある場合
最大値\(\small{ \ f(\beta) \ }\)、最小値\(\small{ \ f(軸) \ }\)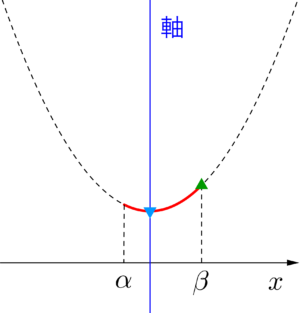
④定義域が軸の左側にある場合
最大値\(\small{ \ f(\beta) \ }\)、最小値\(\small{ \ f(\alpha) \ }\)
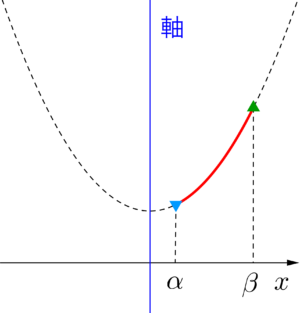
定義域と軸の位置によって最大値や最小値をとる\(\small{ \ x \ }\)が異なるから注意しよう。
次の\(\small{ \ 2 \ }\)次関数の最大値、最小値があればそれを求めよ。またそのときの\(\small{ \ x \ }\)の値も求めよ。
(1)\(\small{ \ y=x^2-6x+5 \ }\)
(2)\(\small{ \ y=2x^2+4x+1 \ (-2\leqq x \leqq 3) \ }\)
(3)\(\small{ \ y=-x^2+2x+1 \ (0 \lt x\lt 2) \ }\)
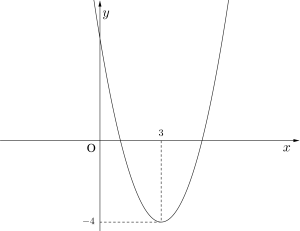
(1)平方完成すると
\(\small{\begin{eqnarray}y=x^2+6x+5\\
=(x-3)^2-4 \ \end{eqnarray}}\)
よって
最小値は\(\small{ \ x=3 \ }\)のとき\(\small{ \ -4 \ }\)
最大値はなし
(2)平方完成すると
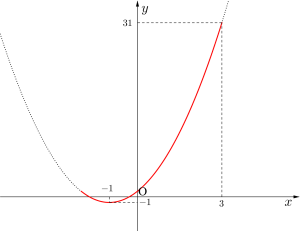
\(\small{\begin{eqnarray}y=2x^2+4x+1\\
=2(x+1)^2-1 \ \end{eqnarray}}\)
よって
最小値は\(\small{ \ x=-1 \ }\)のとき\(\small{ \ -1 \ }\)
最大値は\(\small{ \ x=3 \ }\)のとき\(\small{ \ 31 \ }\)
(3)平方完成すると
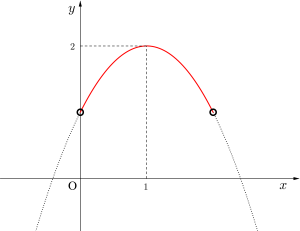
\(\small{\begin{eqnarray}y=-x^2+2x+1\\
=-(x-1)^2+2 \ \end{eqnarray}}\)
よって
最小値はなし
最大値は\(\small{ \ x=1 \ }\)のとき\(\small{ \ 2 \ }\)

だから、軸以外の値を代入するときは一般形に代入するように心がけよう。平方形は分数になる場合が多くて、計算ミスもしやすいからね。
Point 二次関数の最大最小(基本)
①最大最小問題はまずは平方完成する
②軸以外の\(\small{ \ x \ }\)の値を代入するときは一般形に代入する
関数\(\small{ \ y=ax^2-2ax+b(a, \ b \ }\)は定数)は\(\small{ \ (0 \leqq x \leqq 3) \ }\)における最大値が\(\small{ \ 3 \ }\)、最小値が\(\small{ \ -5 \ }\)である。このとき\(\small{ \ a, \ b \ }\)の値の組をすべて求めよ。
平方完成すると
\(\small{\begin{eqnarray} \ y&=&ax^2-2ax+b\\&=&a(x-1)^2-a+b \ \end{eqnarray}}\)
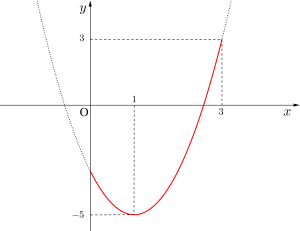
(i)\(\small{ \ a\gt 0 \ }\)のとき
軸の方程式が\(\small{ \ x=1 \ }\)の下に凸の放物線になるので
最小値は\(\small{ \ x=1 \ }\)、最大値は\(\small{ \ x=3 \ }\)のとき
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
-a+b=-5\\
3a+b=3
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて\(\small{ \ a=2, \ b=-3 \ }\)
これは\(\small{ \ a \gt 0 \ }\)を満たす。
(ii)\(\small{ \ a=0 \ }\)のとき
\(\small{ \ y=b \ }\)となり最大値と最小値が一致するから題意を満たさない。
(iii)\(\small{ \ a\lt 0 \ }\)のとき
軸の方程式が\(\small{ \ x=1 \ }\)の上に凸の放物線になるので
最小値は\(\small{ \ x=3 \ }\)、最大値は\(\small{ \ x=1 \ }\)のとき
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
3a+b=-5\\
-a+b=3
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて\(\small{ \ a=-2, \ b=1 \ }\)
これは\(\small{ \ a \lt 0 \ }\)を満たす。
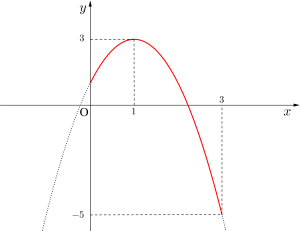
(i)〜(iii)より
\(\small{ \ a=2, \ b=-3 \ }\)、\(\small{ \ a=-2, \ b=1 \ }\)

