こんにちは、リンス(@Lins016)です。
今回は置換を用いた二次関数の最大最小について学習していこう。
四次関数を二次関数に変換して最大値最小値を求める問題
置換が必要な問題を置換しないまま解こうとすると\(\small{ \ x \ }\)の四次関数になってしまうから、微分を利用しないとうまく解くことが出来ないし、微分してもうまく答えを導けない場合がほとんどだから置換することに必ず気付かないといけないよ。
もちろん問題文が\(\small{ \ y=ax^4+bx^3+cx^2+dx+e \ }\)のように展開した形で書いてあることはないから、必ず置換することに気付けるような形で書いてある。
四次関数の問題だったら、二次関数に変換できないか注意して問題文を読もう。
ちなみに現行の教育課程では基本的に四次関数を取り扱うことはないから、四次関数を見たら置換してみようと思うことが大切だ。
・\(\small{ \ y=x^4-2x^2+5 \ }\)の場合
\(\small{ \ t=x^2 \ }\)とすると\(\small{ \ y=t^2-2t+5 \ }\)
・\(\small{ \ y=(x^2-4x)^2+2(x^2-4x)+5 \ }\)の場合
\(\small{ \ t=x^2-4x \ }\)とすると\(\small{ \ y=t^2+2t+5 \ }\)
\(\small{ \ x \ }\)の二次式を\(\small{ \ t \ }\)と置換することで\(\small{ \ t \ }\)の二次関数に変換する
置換した文字の範囲に注意
\(\small{ \ x \ }\)の二次式を\(\small{ \ t \ }\)とおかないと四次関数が二次関数にならないからどの式を置換すれば良いかきちんと考えて置換しよう。
置換して四次関数が二次関数になったら、平方完成して終わりって言いたいところだけど、1つ注意しないといけないことがある。
それは置換した文字の範囲を考えないといけないということ。
高校数学では置換して解く問題って非常に多いけど、置換したら必ず範囲を考えて問題を解くようにしよう。\(\small{ \ t=x^2 \ }\)っておいたら\(\small{ \ t\geqq 0 \ }\)になるから\(\small{ \ t \ }\)は負の値は取らないよね。
次の例題の場合も置換する\(\small{ \ t \ }\)は\(\small{ \ x \ }\)の二次関数だから最大値や最小値が存在することになるよね。置換する文字の範囲に注意して例題を確認してみよう。
\(\small{y=(x^2-2x)^2+4(x^2-2x)+5 \ }\)の最小値を求めよ。
\(\small{y=(x^2-2x)^2+4(x^2-2x)+5}\)
\(\small{t=x^2-2x \ }\)とおくと
\(\small{\begin{eqnarray}y&=&t^2+4t+5\\
&=&(t+2)^2+1\end{eqnarray}}\)
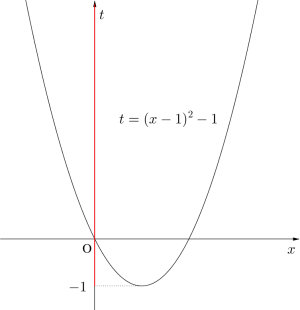
\(\small{t=x^2-2x=(x-1)^2-1}\)より
\(\small{ \ t\geqq-1 \ }\)
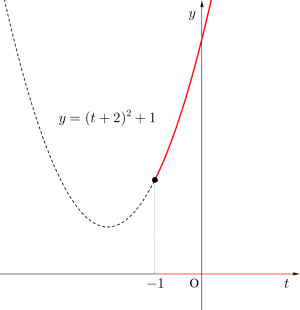
よって最小値は\(\small{ \ t=-1 \quad \therefore x=1\ }\)のとき\(\small{ \ 2 \ }\)となる

Point 置換を用いた二次関数の最大最小
①四次関数の最大最小は置換して二次関数にする
②置換した文字の範囲(最大最小)を求める

