こんにちは、リンス(@Lins016)です。
今回は二項係数について学習していこう。
二項係数とは
二項係数とは二項定理の展開式の各係数のこと。
一般的には\(\small{ \ \binom{ n }{ r } \ }\)と書く。これは\(\small{ \ {}_n\mathrm{ C }_r \ }\)のことで、この値は\(\small{ \ \displaystyle \frac{n!}{r!(n-r)!} \ }\)になる。
二項定理
&=&\displaystyle \sum_{ r = 0}^{ n } {}_n \mathrm{ C }_ra^{n-r}b^r \ \end{eqnarray}}\)
二項係数
\(\small{ \ \binom{ n }{ r }={}_n\mathrm{ C }_r=\displaystyle \frac{n!}{r!(n-r)!} \ }\)
二項係数の性質
①\(\small{ \ {}_ n\mathrm{ C }_r={}_ n\mathrm{ C }_{n-r} \ }\)
②\(\small{ \ {}_ {n+1}\mathrm{ C }_r={}_ n\mathrm{ C }_{r-1}+{}_ n\mathrm{ C }_r \ }\)
二項係数の有名式
②\(\small{ \ 0={}_n \mathrm{ C }_0-{}_n \mathrm{ C }_1+{}_n \mathrm{ C }_2-{}_n \mathrm{ C }_3+{}_n \mathrm{ C }_4-\cdots \ }\)
③\(\small{ \ 2^{n-1}={}_n \mathrm{ C }_0+{}_n \mathrm{ C }_2+{}_n \mathrm{ C }_4+{}_n \mathrm{ C }_6+{}_n \mathrm{ C }_8+\cdots \ }\)
-

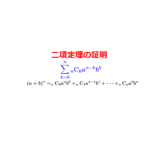
二項定理の証明
数学的帰納法を用いた二項定理の証明について詳しく解説しています。
続きを見る
二項係数の性質
二項係数の性質には次の二つがある。
①二項定理の展開式の初めと終わりからある同じ順番の係数は等しい。
②\(\small{ \ (a+b)^{n+1} \ }\)の展開式の\(\small{ \ r+1 \ }\)番目の項の係数は\(\small{ \ (a+b)^n \ }\)の展開式の\(\small{ \ r \ }\)番目と\(\small{ \ r+1 \ }\)番目の項の係数の和に等しい。
①の証明
\(\small{ \ {}_ n\mathrm{ C }_r=\displaystyle \frac{n!}{r!(n-r)!} \ }\)
\(\small{ \ {}_ n\mathrm{ C }_{n-r}=\displaystyle \frac{n!}{(n-r)!r!} \ }\)
\(\small{ \ \therefore {}_ n\mathrm{ C }_r={}_ n\mathrm{ C }_{n-r} \ }\)
②の証明
\(\small{ \ {}_ n\mathrm{ C }_{r-1}+{}_ n\mathrm{ C }_r\\
=\displaystyle \frac{n!}{(r-1)!(n+1-r)!}+\displaystyle \frac{n!}{r!(n-r)!}\\
=\displaystyle \frac{n!}{(r-1)!(n-r)!}\left(\displaystyle \frac{1}{n+1-r}+\displaystyle \frac{1}{r}\right)\\
=\displaystyle \frac{n!}{(r-1)!(n-r)!}\cdot\displaystyle \frac{n+1}{(n+1-r)r}\\
=\displaystyle \frac{(n+1)!}{r!(n+1-r)!}\\
={}_ {n+1}\mathrm{ C }_r \ }\)
パスカルの三角形
図のように数を並べたものをパスカルの三角形という。
一番左と一番右の数は\(\small{ \ 1 \ }\)で、その他の各数字は左上の数と右上の数の和になっている。
&&&&&&&&\swarrow&&\searrow&&&&&&&\\
n=1\qquad&&&&&&&1&&&&1&&&&&&\\
&&&&&&\swarrow&&\searrow&&\swarrow&&\searrow&&&&&\\
n=2\qquad&&&&&1&&&&2&&&&1&&&&\\
&&&&\swarrow&&\searrow&&\swarrow&&\searrow&&\swarrow&&\searrow&&&\\
n=3\qquad&&&1&&&&3&&&&3&&&&1&&\\
&&\swarrow&&\searrow&&\swarrow&&\searrow&&\swarrow&&\searrow&&\swarrow&&\searrow&\\
n=4\qquad&1&&&&4&&&&6&&&&4&&&&1 \ \end{eqnarray}}\)
この数は二項係数を並べたもので、二項定理\(\small{ \ (a+b)^n \ }\)の展開式の係数を表している。
各数字が左上の数と右上の数の和になっているのは二項係数の性質②を表している。
&&&&&&&&\swarrow&&\searrow&&&&&&&\\
n=1\qquad&&&&&&&{}_1 \mathrm{ C }_0&&&&{}_1 \mathrm{ C }_1&&&&&&\\
&&&&&&\swarrow&&\searrow&&\swarrow&&\searrow&&&&&\\
n=2\qquad&&&&&{}_2 \mathrm{ C }_0&&&&{}_2 \mathrm{ C }_1&&&&{}_2 \mathrm{ C }_2&&&&\\
&&&&\swarrow&&\searrow&&\swarrow&&\searrow&&\swarrow&&\searrow&&&\\
n=3\qquad&&&{}_3 \mathrm{ C }_0&&&&{}_3 \mathrm{ C }_1&&&&{}_3 \mathrm{ C }_2&&&&{}_3 \mathrm{ C }_3&&\\
&&\swarrow&&\searrow&&\swarrow&&\searrow&&\swarrow&&\searrow&&\swarrow&&\searrow&\\
n=4\qquad&{}_4 \mathrm{ C }_0&&&&{}_4 \mathrm{ C }_1&&&&{}_4 \mathrm{ C }_2&&&&{}_4 \mathrm{ C }_3&&&&{}_4 \mathrm{ C }_4 \ \end{eqnarray}}\)

二項係数の有名式
二項定理の\(\small{ \ a, \ b \ }\)に\(\small{ \ 1 \ }\)や\(\small{ \ -1 \ }\)を代入することで有名式を導くことができる。
①\(\small{ \ a=1, \ b=1 \ }\)の場合
②\(\small{ \ a=1, \ b=-1 \ }\)の場合
③①と②を足して