こんにちは、リンス(@Lins016)です。
今回は余弦定理について学習していこう。
余弦定理
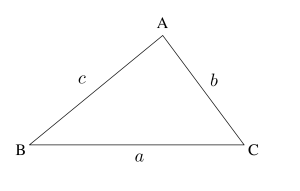
余弦定理は\(\small{ \ \cos \ }\)(余弦)を利用した公式で三角形の3辺から余弦を求めたり、2辺と1つの角からもう1辺を求めることが出来る式になる。
辺を求める場合
\(\small{ \ c^2=a^2+b^2-2ac\cos \mathrm{C} \ }\)
角を求める場合
\(\small{ \ \cos \mathrm{C}=\displaystyle\frac{a^2+b^2-c^2}{2ab} \ }\)
余弦定理の証明も確認しておこう。
余弦定理の利用
余弦定理は\(\small{ \ c^2=a^2+b^2-2ac\cos \mathrm{C} \ }\)を覚えて、これを変形すれば\(\small{ \ \cos \mathrm{C}=\displaystyle\frac{a^2+b^2-c^2}{2ab} \ }\)になるからいいやと思ってる人がよくいるけど、同じ式だけど求める値が違うんだから、しっかりとどちらもパッと出せるようにしておこう。
\(\small{ \ c^2=a^2+b^2-2ac\cos \mathrm{C} \ }\)は辺の長さを求める式として、\(\small{ \ \cos \mathrm{C}=\displaystyle\frac{a^2+b^2-c^2}{2ab} \ }\)は角の大きさを求める式としてきちんと覚えておく必要があるからね。
余弦定理の注意点
余弦定理を利用するとき一つ注意しておくことがある。
まずはこの問題を考えてみよう。
余弦定理を使って
\(\small{ \ \mathrm{BC}^2=2^2+\sqrt{2}^2-2\cdot2\cdot2\cdot\displaystyle\frac{\sqrt{2}}{2}=4 \ }\)
\(\small{ \ \mathrm{BC}=\pm 2 \ }\)
\(\small{ \ \mathrm{BC}\gt 0 \ }\)より\(\small{ \ \mathrm{BC}=2 \ }\)

この形の問題だと答えは1つしかないよね。
それじゃ次の問題を考えてみよう。
余弦定理を使って
\(\small{ \ \mathrm{2}^2=2^2+\mathrm{BC}^2-2\cdot2\cdot\mathrm{BC}\cdot\displaystyle\frac{\sqrt{3}}{2} \ }\)
\(\small{ \ \mathrm{BC}^2-2\sqrt{3}\mathrm{BC}+2=0 \ }\)
\(\small{ \ \therefore \mathrm{BC}=\sqrt{3}\pm1 \ }\)
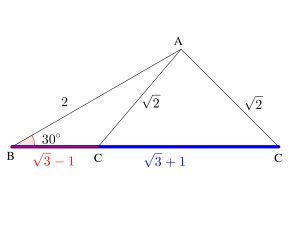
今度はどちらも正の値になるよね。これは\(\small{ \ \sqrt{3}-1 \ }\)でも\(\small{ \ \sqrt{3}+1 \ }\)でも三角形が成り立つんだけど、その場合図のように最大の角が変化したりするから、問題文にその他のヒントがないか注意して答えよう。
つまりこのことから、求める辺の対角とそのはさむ2辺が分かっている場合、求める辺を\(\small{ \ x \ }\)とすると、余弦定理を利用した式は\(\small{ \ x^2=p \gt 0 \ }\)の形になるから答えは一つだよね。
だけど、2辺と求める辺の一端の角が分かっている場合、余弦定理を利用した式は\(\small{ \ x^2+px+q=0 \ }\)の形の二次方程式になるから、答えが正負の場合もあれば、二つとも正の答えになる場合もあるからね。
\(\small{ \ b=6, \ c=4, \ \mathrm{A}=120^{\circ} \ }\)の\(\small{ \ \triangle \mathrm{ABC} \ }\)がある。\(\small{ \ \mathrm{BC} \ }\)の中点を\(\small{ \ \mathrm{M} \ }\)とするとき、次の問いに答えよ。
(1)\(\small{ \ \mathrm{BC} \ }\)の長さ
(2)\(\small{ \ \mathrm{AM} \ }\)の長さ
(1)余弦定理より
\(\small{ \ \mathrm{BC}^2=6^2+4^2-2\cdot6\cdot4\cdot\cos 120^{\circ}=76 \ }\)
\(\small{ \ \therefore \mathrm{BC}=2\sqrt{19} \ }\)
(2)余弦定理より
\(\small{ \ \cos\mathrm{C}=\displaystyle\frac{6^2+\left(2\sqrt{19}\right)^2-4^2}{2\cdot6\cdot2\sqrt{19}}=\displaystyle\frac{4\sqrt{19}}{19} \ }\)
\(\small{ \ \triangle \mathrm{ACM} \ }\)に余弦定理を利用すると
\(\small{ \ \mathrm{AM}^2=6^2+\left(\sqrt{19}\right)^2-2\cdot6\cdot\sqrt{19}\cdot\cos \mathrm{C}=7 \ }\)
\(\small{ \ \therefore \mathrm{AM}=\sqrt{7} \ }\)


Point
①3辺の長さ、2辺と1角がわかっているときは余弦定理を利用
四角形\(\small{ \ \mathrm{ABCD} \ }\)において、\(\small{ \ \angle\mathrm{DAB}=\angle\mathrm{DBC}=90^{\circ} \ }\)、\(\small{ \ \angle\mathrm{BCD}=60^{\circ} \ }\)、\(\small{ \ \mathrm{AB}=\mathrm{AD} \ }\)、\(\small{ \ \mathrm{BC}=1 \ }\)のとき、次の問いに答えよ。
(1)対角線\(\small{ \ \mathrm{BD} \ }\)の長さの\(\small{ \ 2 \ }\)乗\(\small{ \ \mathrm{BD}^2 \ }\)を求めよ。
(2)対角線\(\small{ \ \mathrm{AC} \ }\)の長さの\(\small{ \ 2 \ }\)乗\(\small{ \ \mathrm{AC}^2 \ }\)を求めよ。
(3)\(\small{ \ \angle\mathrm{BAC}=\alpha \ }\)、\(\small{ \ \angle\mathrm{ACD}=\beta \ }\)とおくとき\(\small{ \ \cos^2 \alpha \ }\)と\(\small{ \ \cos^2 \beta \ }\)を求めよ。
(1)直角三角形\(\small{ \ \mathrm{BCD} \ }\)に注目すると
\(\small{ \ \mathrm{BD}=\mathrm{BC}\tan 60^{\circ}=\sqrt{3} \ }\)
\(\small{ \ \therefore \mathrm{BD}^2=3 \ }\)
(2)\(\small{ \ \triangle\mathrm{ABD} \ }\)は\(\small{ \ \mathrm{AB}=\mathrm{AD} \ }\)の直角三角形だから、\(\small{ \ \angle\mathrm{ABD}=\angle\mathrm{ADB}=45^{\circ} \ }\)
\(\small{ \ \therefore \mathrm{AB}=\mathrm{AD}=\mathrm{BD}\cos 45^{\circ}=\sqrt{\displaystyle\frac{3}{2}} \ }\)
\(\small{ \ \triangle\mathrm{ABC} \ }\)に余弦定理を利用して
&=&\displaystyle\frac{5}{2}+\sqrt{3} \ \end{eqnarray}}\)
(3)\(\small{ \ \triangle\mathrm{ABC} \ }\)に余弦定理を利用して
\(\small{\begin{eqnarray} \ \cos \alpha&=&\displaystyle\frac{\displaystyle\frac{3}{2}+\left(\displaystyle\frac{5}{2}+\sqrt{3}\right)-1^2}{2\sqrt{\displaystyle\frac{3}{2}}\sqrt{\displaystyle\frac{5}{2}+\sqrt{3}}}\\
&=&\displaystyle\frac{\sqrt{3}+1}{\sqrt{5+2\sqrt{3}}} \ \end{eqnarray}}\)
\(\small{ \ \therefore \cos^2 \alpha =\displaystyle\frac{\left(\sqrt{3}+1\right)^2}{5+2\sqrt{3}}=\displaystyle\frac{8+2\sqrt{3}}{13} \ }\)
\(\small{ \ \mathrm{CD}=\displaystyle\frac{\mathrm{BC}}{\cos 60^{\circ}}=2 \ }\)より
\(\small{ \ \triangle\mathrm{ACD} \ }\)に余弦定理を利用して
\(\small{\begin{eqnarray} \ \cos \beta&=&\displaystyle\frac{2^2+\left(\displaystyle\frac{5}{2}+\sqrt{3}\right)-\displaystyle\frac{3}{2}}{2\cdot2\cdot\sqrt{\displaystyle\frac{5}{2}+\sqrt{3}}}\\
&=&\displaystyle\frac{5+\sqrt{3}}{4\sqrt{\displaystyle\frac{5}{2}+\sqrt{3}}} \ \end{eqnarray}}\)
\(\small{ \ \therefore \cos^2 \beta=\displaystyle\frac{\left(5+\sqrt{3}\right)^2}{16\left(\displaystyle\frac{5}{2}+\sqrt{3}\right)}=\displaystyle\frac{40-3\sqrt{3}}{52} \ }\)


