こんにちは、リンス(@Lins016)です。
今回は三角関数の最大最小(合成の利用)について学習していこう。
合成を利用した三角関数の最大値と最小値
前回二次関数への置換で三角関数の最大最小を求める問題をやったけど今回は合成を利用する最大最小について考えていこう。
まずは合成について以前の記事で確認しておこう。
・合成
\(\small{\begin{eqnarray} \ y&=&a\sin x+b\cos x\\
&=&R\sin\left(x+\alpha\right) \ \end{eqnarray}}\)
・二倍角の合成
&=&a\cdot\displaystyle\frac{1-\cos2x}{2}+b\cdot\displaystyle\frac{1}{2}\sin2x+c\cdot\displaystyle\frac{1+\cos2x}{2}\\
&=&A\sin2x+B\cos2x+C\\
&=&R\sin\left(2x+\alpha\right)+C \ \end{eqnarray}}\)
合成を利用した最大最小の基本
\(\small{ \ y=\sin x+\cos x \ }\)の最大値と最小値について考えてみよう。
\(\small{ \ \sin x \ }\)と\(\small{ \ \cos x \ }\)の偏角が同じものの和や差は合成することができるんだったよね。
だから\(\small{ \ y=\sin x+\cos x \ }\)は
\(\small{\begin{eqnarray} \ y&=&\sin x+\cos x\\
&=&\sqrt{2}\sin\left(x+\displaystyle\frac{\pi}{4}\right) \ \end{eqnarray}}\)
になる。
これを\(\small{ \ x \ }\)の範囲を\(\small{ \ 0\leqq x \lt 2\pi \ }\)と\(\small{ \ 0\leqq x \leqq \pi \ }\)の場合に分けて考えてみよう。
①\(\small{ \ 0\leqq x \lt 2\pi \ }\)のとき
\(\small{ \ \displaystyle\frac{\pi}{4}\leqq x+\displaystyle\frac{\pi}{4} \lt \displaystyle\frac{9}{4}\pi \ }\)より
\(\small{ \ -1\leqq \sin\left(x+\displaystyle\frac{\pi}{4}\right)\leqq 1 \ }\)になる。
だから\(\small{ \ y=\sqrt{2}\sin\left(x+\displaystyle\frac{\pi}{4}\right) \ }\)は
最大値\(\small{ \ \sqrt{2} \ }\)
最小値\(\small{ \ -\sqrt{2} \ }\)になるよね。
最大値\(\small{ \ \sqrt{2} \ }\)のとき
\(\small{ \ \sin\left(x+\displaystyle\frac{\pi}{4}\right)=1 \ }\)から\(\small{ \ x=\displaystyle\frac{\pi}{4} \ }\)
最小値\(\small{ \ -\sqrt{2} \ }\)のとき
\(\small{ \ \sin\left(x+\displaystyle\frac{\pi}{4}\right)=-1 \ }\)から\(\small{ \ x=\displaystyle\frac{5}{4}\pi \ }\)

②\(\small{ \ 0\leqq x \leqq \pi \ }\)のとき
\(\small{ \ \displaystyle\frac{\pi}{4}\leqq x+\displaystyle\frac{\pi}{4} \leqq \displaystyle\frac{5}{4}\pi \ }\)より単位円を利用して考えると\(\small{ \ \sin \ }\)は単位円の動径の\(\small{ \ y \ }\)座標だから\(\small{ \ -\displaystyle\frac{\sqrt{2}}{2}\leqq \sin\left(x+\displaystyle\frac{\pi}{4}\right)\leqq 1 \ }\)になるよね。
だから\(\small{ \ y=\sqrt{2}\sin\left(x+\displaystyle\frac{\pi}{4}\right) \ }\)は
最大値\(\small{ \ \sqrt{2} \ }\)
最小値\(\small{ \ -1 \ }\)になるよね。
最大値\(\small{ \ \sqrt{2} \ }\)のとき
\(\small{ \ \sin\left(x+\displaystyle\frac{\pi}{4}\right)=1 \ }\)から\(\small{ \ x=\displaystyle\frac{\pi}{4} \ }\)
最小値\(\small{ \ -1 \ }\)のとき
\(\small{ \ \sin\left(x+\displaystyle\frac{\pi}{4}\right)=-\displaystyle\frac{\sqrt{2}}{2} \ }\)から\(\small{ \ x=\pi \ }\)
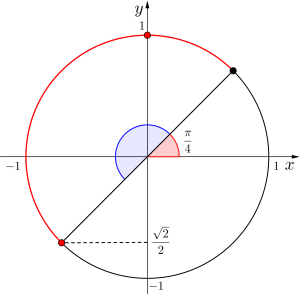
\(\small{ \ 0\leqq x \lt 2\pi \ }\)のとき\(\small{ \ \displaystyle\frac{\pi}{4}\leqq x+\displaystyle\frac{\pi}{4} \lt \displaystyle\frac{9}{4}\pi \ }\)で単位円を一周するから\(\small{ \ -1\leqq \sin\left(x+\displaystyle\frac{\pi}{4}\right)\leqq 1 \ }\)になるけど、\(\small{ \ 0\leqq x \leqq \pi \ }\)のときは\(\small{ \ \displaystyle\frac{\pi}{4}\leqq x+\displaystyle\frac{\pi}{4} \leqq \displaystyle\frac{5}{4}\pi \ }\)で単位円を半周しかしないから、\(\small{ \ -\displaystyle\frac{\sqrt{2}}{2}\leqq \sin\left(x+\displaystyle\frac{\pi}{4}\right)\leqq 1 \ }\)になるよね。
範囲がある場合は単位円を利用して最大値最小値を考えよう。
合成の角が有名角じゃない場合
上の問題では有名角で合成することができたけど、問題によっては有名角にならない場合もある。
次は\(\small{ \ y=2\sin x+3\cos x \ }\)の最大値と最小値について考えてみよう。
まずはこの式を合成すると
\(\small{\begin{eqnarray} \ y&=&2\sin x+3\cos x\\
&=&\sqrt{13}\left(\displaystyle\frac{2}{\sqrt{13}}\sin x+\displaystyle\frac{3}{\sqrt{13}}\cos x\right)\\
&=&\sqrt{13}\sin\left(x+\alpha\right) \ \end{eqnarray}}\)
ここで\(\small{ \ \alpha \ }\)は\(\small{ \ \sin\alpha=\displaystyle\frac{3}{\sqrt{13}}, \ \cos\alpha=\displaystyle\frac{2}{\sqrt{13}} \ }\)を満たす角になる。
\(\small{ \ \alpha \ }\)が有名角にならない場合は上の赤字の部分のように\(\small{ \ \alpha \ }\)がどんな角か言っておく必要があるからね。
それじゃ今度も\(\small{ \ x \ }\)の範囲を\(\small{ \ 0\leqq x \lt 2\pi \ }\)と\(\small{ \ 0\leqq x \leqq \pi \ }\)の場合に分けて考えてみよう。
①\(\small{ \ 0\leqq x \lt 2\pi \ }\)のとき
\(\small{ \ \alpha\leqq x+\alpha \lt 2\pi+\alpha \ }\)より
\(\small{ \ -1\leqq \sin\left(x+\alpha\right)\leqq 1 \ }\)になる。
だから\(\small{ \ y=\sqrt{13}\sin\left(x+\alpha\right) \ }\)は
最大値\(\small{ \ \sqrt{13} \ }\)
最小値\(\small{ \ -\sqrt{13} \ }\)になるよね。
最大値\(\small{ \ \sqrt{13} \ }\)のとき
\(\small{ \ \sin\left(x+\alpha\right)=1 \ }\)から\(\small{ \ x=\displaystyle\frac{\pi}{2}-\alpha \ }\)
最小値\(\small{ \ -\sqrt{13} \ }\)のとき
\(\small{ \ \sin\left(x+\alpha\right)=-1 \ }\)から\(\small{ \ x=\displaystyle\frac{3}{2}\pi-\alpha \ }\)

\(\small{ \ \alpha \ }\)は\(\small{ \ \sin\alpha=\displaystyle\frac{3}{\sqrt{13}}, \ \cos\alpha=\displaystyle\frac{2}{\sqrt{13}} \ }\)を満たす角だから正確な値は言えないからこの言い方なるからね。
②\(\small{ \ 0\leqq x \leqq \pi \ }\)のとき
\(\small{ \ \alpha\leqq x+\alpha \leqq \pi+\alpha \ }\)より単位円を利用して考えると\(\small{ \ \sin \ }\)は単位円の動径の\(\small{ \ y \ }\)座標だから\(\small{ \ -\displaystyle\frac{3}{\sqrt{13}}\leqq \sin\left(x+\alpha \right)\leqq 1 \ }\)になる。
だから\(\small{ \ y=\sqrt{13}\sin\left(x+\alpha\right) \ }\)は
最大値\(\small{ \ \sqrt{13} \ }\)
最小値\(\small{ \ -3 \ }\)になる。
最大値\(\small{ \ \sqrt{13} \ }\)のとき
\(\small{ \ \sin\left(x+\alpha\right)=1 \ }\)から\(\small{ \ x=\displaystyle\frac{\pi}{2}-\alpha \ }\)
ただし\(\small{ \ \alpha \ }\)は\(\small{ \ \alpha \ }\)は\(\small{ \ \sin\alpha=\displaystyle\frac{3}{\sqrt{13}}, \ \cos\alpha=\displaystyle\frac{2}{\sqrt{13}} \ }\)を満たす角
最小値\(\small{ \ -3 \ }\)のとき
\(\small{ \ \sin\left(x+\alpha\right)=-\displaystyle\frac{3}{\sqrt{13}} \ }\)から\(\small{ \ x=\pi \ }\)
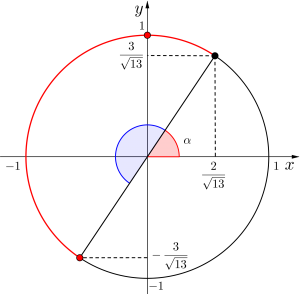
最小値をとるのは単位円から\(\small{ \ x=\pi \ }\)のときってわかるよね。そのときの値は\(\small{ \ y=\sqrt{13}\sin\left(\pi+\alpha\right) \ }\)になるけど\(\small{ \ \sin\left(\pi+\alpha\right)=-\sin\alpha \ }\)だし、合成したときに\(\small{ \ \alpha \ }\)は\(\small{ \ \sin\alpha=\displaystyle\frac{3}{\sqrt{13}} \ }\)を満たす角って定めているから\(\small{ \ -\sin\alpha=-\displaystyle\frac{3}{\sqrt{13}} \ }\)になるからね。
だから有名角じゃない値でも\(\small{ \ \sin\alpha \ }\)や\(\small{ \ \cos\alpha \ }\)がわかっていれば最大値や最小値を\(\small{ \ \alpha \ }\)を利用した値で求めることができるから覚えておこう。
二倍角の合成
次は\(\small{ \ 2x \ }\)の合成について考えていこう。
\(\small{ \ 2x \ }\)の合成って言っても\(\small{ \ y=\sin2x+\cos2x \ }\)のような問題じゃなくて、\(\small{ \ \sin^2x, \ \cos^2x, \ \sin x\cos x \ }\)で作られた関数の問題なんだ。
この問題は\(\small{ \ 2x \ }\)の合成ってわかってないと、\(\small{ \ \sin x=t \ }\)と置換してみたり色々試すことになるんだけど、うまくいかないから時間だけが過ぎて結局解けないんだ。
だから二倍角の合成を利用することを覚えておかないといけない。
だから\(\small{ \ \sin^2x, \ \cos^2x, \ \sin x\cos x \ }\)の三つの項で作られた関数は\(\small{ \ 2x \ }\)の合成って覚えておこう。
\(\small{ \ \cos2x=1-2\sin^2x \ }\)から\(\small{ \ \sin^2x=\displaystyle \frac{1-\cos 2x}{2} \ }\)
\(\small{ \ \cos2x=2\cos^2-1 \ }\)から\(\small{ \ \cos^2x=\displaystyle \frac{1+\cos2x}{2} \ }\)
\(\small{ \ \sin2x=2\sin x\cos x \ }\)から、\(\small{ \ \sin x\cos x=\displaystyle \frac{1}{2}\sin2x \ }\)
これを利用することで
\(\small{\begin{eqnarray} &&\sin^2x+2\sqrt{3}\sin x\cos x+3\cos^2x\\[5pt]
&&=\displaystyle\frac{1-\cos2x}{2}+\sqrt{3}\sin2x+3\cdot\displaystyle\frac{1+\cos2x}{2}\\
&&=\sqrt{3}\sin2x+\cos2x+2\\
&&=2\left(\displaystyle\frac{\sqrt{3}}{2}\sin2x+\displaystyle\frac{1}{2}\cos2x\right)+2\\
&&=2\sin\left(2x+\displaystyle\frac{\pi}{6}\right)+2 \ \end{eqnarray}}\)
って変形できるよね。
これって覚えてないと、この形に変形できないからね。
三角関数の最大最小ってそんなに多くないからこの形は必ず覚えておこう。
ちなみに\(\small{ \ \sin^2x, \ \cos^2x, \ \sin x\cos x \ }\)って言ったけど、\(\small{ \ \sin^2x+\cos^2x=1 \ }\)だから \(\small{ \ \sin^2x, \ \sin x\cos x \ }\)や\(\small{ \ \ \cos^2x, \ \sin x\cos x \ }\)でもこの形になるからね。
次の関数の最大値と最小値を求めよ。
ただし、\(\small{ \ 0\leqq x \leqq \displaystyle\frac{\pi}{2} \ }\)とする。
(1)\(\small{ \ y=3\sin x+\sqrt{3}\cos x \ }\)
(2)\(\small{ \ y=5\cos^2x+6\sqrt{3}\sin x\cos x-3\sin^2x \ }\)
(1)
\(\small{\begin{eqnarray} \ y&=&3\sin x+\sqrt{3}\cos x\\
&=&2\sqrt{3}\left(\displaystyle\frac{\sqrt{3}}{2}\sin x+\displaystyle\frac{1}{2}\cos x\right)\\
&=&2\sqrt{3}\left(\sin x+\displaystyle\frac{\pi}{6}\right) \ \end{eqnarray}}\)
\(\small{ \ 0\leqq x \leqq \displaystyle\frac{\pi}{2} \ }\)より
\(\small{ \ \displaystyle\frac{\pi}{6}\leqq x+\displaystyle\frac{\pi}{6} \leqq \displaystyle\frac{2}{3}\pi \ }\)
最大値\(\small{ \ 2\sqrt{3}\left(x=\displaystyle\frac{\pi}{3}\right) \ }\)
最小値\(\small{ \ \sqrt{3}\left(x=0\right) \ }\)

(2)
&=&5\cdot\displaystyle\frac{1+\cos2x}{2}+6\cdot\displaystyle\frac{1}{2}\sin2x-3\cdot\displaystyle\frac{1-\cos2x}{2}\\
&=&3\sin2x+4\cos2x+1\\
&=&5\left(\displaystyle\frac{3}{5}\sin2x-\displaystyle\frac{4}{5}\cos2x\right)+1\\
&=&5\sin\left(2x+\alpha\right)+1 \ \end{eqnarray}}\)
ここで\(\small{ \ \alpha \ }\)は
\(\small{ \ \sin\alpha=\displaystyle\frac{4}{5}, \ \cos\alpha=\displaystyle\frac{3}{5} \ }\)を満たす角
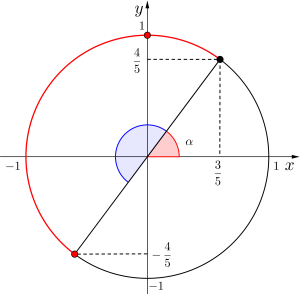
\(\small{ \ 0\leqq x \leqq \displaystyle\frac{\pi}{2} \ }\)より
\(\small{ \ \alpha\leqq 2x+\alpha \leqq \pi+\alpha \ }\)より
最大値\(\small{ \ 6 \ }\)
最小値\(\small{ \ -3 \ }\)

Point 三角関数の最大最小(合成の利用)
①\(\small{ \ \sin \ }\)と\(\small{ \ \cos \ }\)の和は合成を利用する
②単位円から最大値最小値を求める
\(\small{ \ f(x)=a\sin^2x+b\cos^2x+c\sin x\cos x \ }\)の最大値が\(\small{ \ 2 \ }\)、最小値が\(\small{ \ -1 \ }\)になるとき\(\small{ \ a, \ b, \ c \ }\)を求めよ。ただし、\(\small{ \ a \ }\)は整数、\(\small{ \ b, \ c \ }\)は実数とする。
\(\small{ \ f(x) \ }\)を変形すると
&=&a\cdot\displaystyle\frac{1-\cos2x}{2}+b\cdot\displaystyle\frac{1+\cos2x}{2}+c\cdot\displaystyle\frac{1}{2}\sin2x\\
&=&\displaystyle\frac{c}{2}\sin2x+\displaystyle\frac{b-a}{2}\cos2x+\displaystyle\frac{a+b}{2}\\
&=&\sqrt{\left(\displaystyle\frac{c}{2}\right)^2+\left(\displaystyle\frac{b-a}{2}\right)^2}\sin\left(2x+\alpha\right)+\displaystyle\frac{a+b}{2} \ \end{eqnarray}}\)
ただし\(\small{ \ \alpha \ }\)は
\cos\alpha=\displaystyle\frac{\displaystyle\frac{c}{2}}{\sqrt{\left(\displaystyle\frac{c}{2}\right)^2+\left(\displaystyle\frac{b-a}{2}\right)^2}}=\displaystyle\frac{c}{\sqrt{c^2+(b-a)^2}} \ }\)
を満たす角
\(\small{ \ x \ }\)に制限はないので
\(\small{ \ -1\leqq \sin\left(2x+\alpha\right) \leqq 1 \ }\)
よって
最大値\(\small{ \ \sqrt{\left(\displaystyle\frac{c}{2}\right)^2+\left(\displaystyle\frac{b-a}{2}\right)^2}+\displaystyle\frac{a+b}{2} \ }\)
最小値\(\small{ \ -\sqrt{\left(\displaystyle\frac{c}{2}\right)^2+\left(\displaystyle\frac{b-a}{2}\right)^2}+\displaystyle\frac{a+b}{2} \ }\)
\left\{
\begin{array}{l}
\sqrt{\left(\displaystyle\frac{c}{2}\right)^2+\left(\displaystyle\frac{b-a}{2}\right)^2}+\displaystyle\frac{a+b}{2}=2\\
-\sqrt{\left(\displaystyle\frac{c}{2}\right)^2+\left(\displaystyle\frac{b-a}{2}\right)^2}+\displaystyle\frac{a+b}{2}=-1
\end{array}
\right.
\end{eqnarray} \ }\)
上の式をそれぞれ足した式と引いた式は
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
a+b=1\\
\sqrt{c^2+(b-a)^2}=3
\end{array}
\right.
\end{eqnarray} \ }\)
これより
\(\small{ \ c^2+(b-a)^2=9 \ }\)
\(\small{ \ c^2+(1-2a)^2=9 \ }\)
\(\small{ \ c \ }\)は実数より
\(\small{ \ c^2=9-(1-2a)^2\geqq0 \ }\)
\(\small{ \ \therefore 4a^2-4a-8 \leqq0 \ }\)
\(\small{ \ (a+1)(a-2)\leqq0 \ }\)
\(\small{ \ \therefore -1 \leqq a \leqq 2 \ }\)
\(\small{ \ a \ }\)は整数より\(\small{ \ a=-1, \ 0, \ 1, \ 2 \ }\)
これより
\(\small{ \ \begin{eqnarray}
(a, \ b, \ c)
=
\begin{cases}
(-1,\ 2, \ 0 )\\
(0, \ 1, \ \pm2\sqrt{2})\\
(1, \ 0, \ \pm2\sqrt{2})\\
(2, \ -1, \ 0)
\end{cases}
\end{eqnarray} \ }\)

