こんにちは、リンス(@Lins016)です。
今回は集合と集合の記号について学習していこう。
集合の記号の意味を理解しよう
集合には様々な記号が出てくるけど、みんなきちんと覚えてるかな?
なんとなく覚えてるけど・・・って人が多いんじゃないかな。この機会にきちんと記号とその意味を理解しておこう。
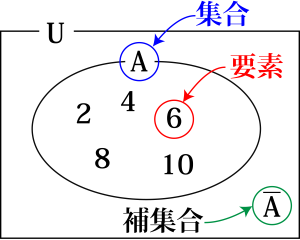

集合とは
集合ってある条件を満たしていて、他のものときちんと区別できるものの集まりの事だよね。
今さら説明なんていらないと思うけど、一応。。。
集合を作る条件は様々で、高校数学では「\(\small{ \ 2 \ }\)で割り切れる数の集まり」や「\(\small{ \ 1 \ }\)から\(\small{ \ 10 \ }\)までの整数」のようないろいろな条件がある。
これを満たすものの集まりを集合っていうからね。
数学じゃないところでは、果物や野菜って言うのも集合の一種とも言えるよね。
集合の要素
集合を作る個々のものを集合の要素っていうから覚えておこう。
「\(\small{ \ a \ }\)は\(\small{ \ A \ }\)の要素である」ってことを\(\small{ \ a \in A \ }\)って書くからね。
「\(\small{ \ a \ }\)が\(\small{ \ A \ }\)の要素でない」場合は\(\small{ \ a \notin A \ }\)って書く。
集合の書き方
集合の書き方って二通りあるからそれをきちんと覚えておこう。
まずは要素を書き並べる書き方で
\(\small{ \ A=\left\{2, \ 4, \ 6, \ 8, \ 10 \right\} \ }\)
のように中括弧の中に要素を書き並べればいいんだ。
ただ、この方法じゃ要素がたくさんある場合書くのが大変だよね。
そこで条件を書く書き方があるんだ。
\(\small{ \ A=\left\{x \ | \ 1\leqq x\leqq10, \ xは整数\right\} \ }\)
のように書く。
これは、集合\(\small{ \ A \ }\)は「|」の左側の文字の要素で作られて、その要素は「|」の右側の条件を満たすすべてのものってことになるから、この書き方は覚えておこう。
要素の数が少なくて整数だけの場合は書き出す方法でもいいけど、整数だけじゃなく\(\small{ \ 1\leqq x \leqq 10 \ }\)とかの整数以外の範囲が必要な場合は条件を書く方法じゃないと表すことができないからね。
ちなみに条件の書き方は、数式(等式や不等式など)だけじゃなく、文章で表されることも多いからね。
部分集合とは
集合\(\small{ \ B \ }\)の要素がすべて集合\(\small{ \ A \ }\)の要素になっているとき、
「\(\small{ \ B \ }\)は\(\small{ \ A \ }\)の部分集合である」といって記号\(\small{ \ B\subset A \ }\)って書くから覚えておこう。
集合\(\small{ \ B \ }\)は集合\(\small{ \ A \ }\)に含まれるってことを意味するからね。
\(\small{ \ A \supset B \ }\)って逆に書いてある場合もあるけど、意味は同じだからね。

また\(\small{ \ B\subset A \ }\)かつ\(\small{ \ A\subset B \ }\)のとき\(\small{ \ A=B \ }\)になる。
これは集合\(\small{ \ A \ }\)の要素と集合\(\small{ \ B \ }\)の要素が全く同じってことだからね。
(1)集合\(\small{ \ A=\left\{p, \ q, \ r\right\} \ }\)の部分集合をすべてかけ。
(2)\(\small{ \ A=\left\{3n-1 \ | \ 1\leqq n \leqq 5, \ nは整数\right\} \ }\)、\(\small{ \ B=\left\{6n+2 \ | \ 0\leqq n \leqq 2, \ nは整数\right\} \ }\)のとき、\(\small{ \ 2 \ }\)つの集合\(\small{ \ A, \ B \ }\)に成り立つ関係を記号\(\small{ \ \subset \ }\)を用いて表せ。
(1)\(\small{ \left\{p\right\} }\)、\(\small{ \left\{q\right\} }\)、\(\small{ \left\{r\right\} }\)、\(\small{ \left\{p, \ q\right\} }\)、\(\small{ \left\{p,r\right\} }\)、\(\small{ \left\{q, \ r\right\} }\)、\(\small{ \left\{p, \ q, \ r\right\} }\)、\(\small{ \left\{\varnothing\right\} }\)
(2)
\(\small{ \ A=\left\{3n-1 \ | \ 1\leqq n \leqq 5, \ nは整数\right\} \ }\)より、\(\small{ \ A=\left\{ 2, \ 5, \ 8, \ 11, \ 14\right\}\ }\)
\(\small{ \ B=\left\{6n+2 \ | \ 0\leqq n \leqq 2, \ nは整数\right\} \ }\)より、\(\small{ \ B=\left\{ 2, \ 8, \ 14\right\}\ }\)
よって\(\small{ \ B\subset A \ }\)

これも部分集合の一つになるから注意しよう。
おまけ 真部分集合とは
高校数学で部分集合は\(\small{ \ B\subset A \ }\)って表すけど、この記号の書き方は本来「真部分集合」って言って、\(\small{ \ A=B \ }\)のものは除くんだ。
つまり、集合\(\small{ \ B \ }\)の要素はすべて集合\(\small{ \ A \ }\)に含まれてかつ集合\(\small{ \ A \ }\)には集合\(\small{ \ B \ }\)の要素以外の要素があることを真部分集合っていうんだ。
だから\(\small{ \ A=B \ }\)になるもの含んだ部分集合は\(\small{ \ B \subseteqq A \ }\)や\(\small{ \ B \subseteq A \ }\)って書き方をするんだ。
でも現行の高校数学の部分集合は\(\small{ \ B\subset A \ }\)の記号で\(\small{ \ A=B \ }\)を含んだものを部分集合として学習しているから注意しよう。
全体集合とは補集合とは
一つの集合\(\small{ \ U \ }\)を定めて、その集合\(\small{ \ U \ }\)の部分集合を考える問題がほとんどで、この集合\(\small{ \ U \ }\)のことを全体集合っていう。
問題で見ると「\(\small{ \ 1 \ }\)から\(\small{ \ 100 \ }\)までの整数のうち・・・・」といった最初に全体集合が定められていることがほとんどだよね。
また、集合\(\small{ \ U \ }\)から集合\(\small{ \ A \ }\)の要素を取り除いた集合を補集合といい、\(\small{ \ \overline{A} \ }\)って書くから覚えておこう。
これはよく使うからね。
有名な集合「自然数、整数、有理数、実数、複素数」
数学でよく使う集合として、「自然数、整数、有理数、実数、複素数」がある。
高校一年生だとまだ複素数は教わっていないかもしれないけどこの五つの集合には次の関係があるから覚えておこう。
\(\small{ \ \mathbb{ N } \ }\):自然数全体の集合
\(\small{ \ \mathbb{ Z } \ }\):整数全体の集合
\(\small{ \ \mathbb{ Q } \ }\):有理数全体の集合
\(\small{ \ \mathbb{ R } \ }\):実数全体の集合
\(\small{ \ \mathbb{ C } \ }\):複素数全体の集合
\(\large{ \ \mathbb{ N } \subset \mathbb{ Z } \subset \mathbb{ Q } \subset \mathbb{ R } \subset \mathbb{ C } \ }\)

自分で答案に集合を定めるときはこのルールにしたがって大文字と小文字でかき分けよう。
Point
①\(\small{ \ a \in A \ }\)は\(\small{ \ a \ }\)は集合\(\small{ \ A \ }\)の要素
②\(\small{ \ B\subset A \ }\)は集合\(\small{ \ B \ }\)は集合\(\small{ \ A \ }\)の部分集合
③\(\small{ \ \overline{A} \ }\)は集合\(\small{ \ A \ }\)の補集合

