こんにちは、リンス(@Lins016)です。
今回は集合の要素の個数について学習していこう。
集合の要素の個数
集合の要素の個数を求める場合、ベン図を利用しよう。視認性に優れてるから問題を考えやすくしてくれるからね。
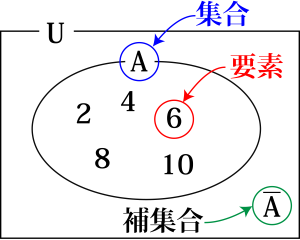
要素の個数
部分集合\(\small{ \ \mathrm{A} \ }\)に属する要素の個数
\(\small{ \ n(\mathrm{A})=5 \ }\)
要素の記号と要素の個数の記号
集合は\(\small{ \ \mathrm{A}=\left\{2, \ 4, \ 6, \ 8, \ 10 \right\} \ }\)のように要素を書き並べる場合と、\(\small{ \ \mathrm{A}=\left\{x \ | \ 1\leqq x\leqq10, \ xは偶数\right\} \ }\)のように要素の条件を書く場合があったよね。
忘れている人は再度チェックしておこう。
要素の個数は集合の記号と合わせて\(\small{ \ n(\mathrm{A})=50 \ }\)のように\(\small{ \ n \ }\)の後ろの括弧内に集合の記号を書くんだ。
\(\small{ \ n(\mathrm{A})=50 \ }\)は集合\(\small{ \ \mathrm{A} \ }\)の要素が\(\small{ \ 50 \ }\)個あることを示している。
\(\small{ \ n(\mathrm{A}) \ }\)は数字だから、\(\small{ \ n(\mathrm{A})+n(\overline{\mathrm{A}})=n(\mathrm{U}) \ }\)のような式も成り立つからね。
ベン図と集合
ベン図と集合の記号を考えてみよう。全体集合\(\small{ \ \mathrm{U} \ }\)と二つの部分集合\(\small{ \ \mathrm{A} \ }\)、\(\small{ \ \mathrm{B} \ }\)が図のように一部重なっている場合、\(\small{ \ \mathrm{A} \ }\)にも\(\small{ \ \mathrm{B} \ }\)にも属している要素の個数は\(\small{ \ n\left(\mathrm{A}\cap \mathrm{B}\right) \ }\)ってかくことができるよね。
集合の問題はベン図を利用して集合の要素の数を考えよう。そのためにもベン図の書き方や使い方をきちんと学習しておかないといけないよ。
このサイトでは斜線を利用してベン図を書くことを推奨しているからチェックしておこう。
\(\small{ \ 1 \ }\)から\(\small{ \ 100 \ }\)までの整数のうち次のような数は何個あるか。
(1)\(\small{ \ 8 \ }\)の倍数
(2)\(\small{ \ 12 \ }\)の倍数
(3)\(\small{ \ 8 \ }\)の倍数であるが\(\small{ \ 12 \ }\)の倍数でない整数
(4)\(\small{ \ 8 \ }\)でも\(\small{ \ 12 \ }\)でも割り切れない整数
(1)\(\small{ \ 100 \div 8=12 \ }\)余り\(\small{ \ 4 \ }\)
よって\(\small{ \ 8 \ }\)の倍数は\(\small{ \ 12 \ }\)個
(2)\(\small{ \ 100 \div 12=8 \ }\)余り\(\small{ \ 4 \ }\)
よって\(\small{ \ 12 \ }\)の倍数は\(\small{ \ 8 \ }\)個
(3)\(\small{ \ 8 \ }\)の倍数の集合を\(\small{ \ \mathrm{A} \ }\)
\(\small{ \ 12 \ }\)の倍数の集合を\(\small{ \ \mathrm{B} \ }\)とする
\(\small{ \ 8 \ }\)の倍数であるが\(\small{ \ 12 \ }\)の倍数でない整数の集合は\(\small{ \ \mathrm{A}\cap \overline{\mathrm{B}} \ }\)
\(\small{ \ n\left(\mathrm{A}\cap \overline{\mathrm{B}}\right)=n(\mathrm{A})-n\left(\mathrm{A}\cap\mathrm{B}\right) \ }\)
ここで\(\small{ \ \mathrm{A}\cap\mathrm{B} \ }\)は\(\small{ \ 24 \ }\)の倍数の集合より
\(\small{ \ 100\div 24=4 \ }\)余り\(\small{ \ 4 \ }\)
\(\small{ \ n\left(\mathrm{A}\cap\mathrm{B}\right)=4 \ }\)
\(\small{\begin{eqnarray} \ n\left(\mathrm{A}\cap \overline{\mathrm{B}}\right)&=&n(\mathrm{A})-n\left(\mathrm{A}\cap\mathrm{B}\right)\\
&=&12-4=8 \ \end{eqnarray}}\)
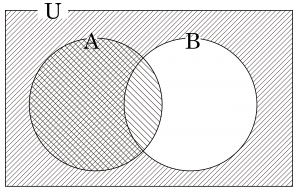
(4)\(\small{ \ 8 \ }\)でも\(\small{ \ 12 \ }\)でも割り切れない
整数の集合は\(\small{ \ \overline{\mathrm{A}}\cap \overline{\mathrm{B}} \ }\)
\(\small{\begin{eqnarray} \ n\left(\overline{\mathrm{A}}\cap \overline{\mathrm{B}}\right)&=&n\left(\overline{\mathrm{A}\cup\mathrm{B}}\right)\\
&=&n\left(\mathrm{U}\right)-n\left(\mathrm{A}\cup\mathrm{B}\right)\\
&=&100-12-8+4\\
&=&84 \ \end{eqnarray}}\)
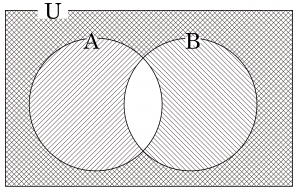

これをド・モルガンの法則っていうからね。
集合の要素の個数の取りうる範囲
次に集合の要素の個数の取りうる範囲について考えてみよう。
全体集合に二つの部分集合\(\small{ \ \mathrm{A} \ }\)と\(\small{ \ \mathrm{B} \ }\)がある場合、\(\small{ \ \mathrm{A} \ }\)にも\(\small{ \ \mathrm{B} \ }\)にも属する集合の要素の個数\(\small{ \ n\left(\mathrm{A}\cap \mathrm{B}\right) \ }\)とどちらにも属さない集合の要素の個数\(\small{ \ n\left(\overline{\mathrm{A}\cup \mathrm{B}}\right) \ }\)を考えてみよう。
\(\small{ \ \mathrm{A} \ }\)にも\(\small{ \ \mathrm{B} \ }\)にも属する集合の要素の個数\(\small{ \ n\left(\mathrm{A}\cap \mathrm{B}\right) \ }\)が最も大きくなるのは、図のように一つの部分集合にもう一つの部分集合がすべて属している場合なんだ。
このとき、\(\small{ \ \mathrm{A} \ }\)にも\(\small{ \ \mathrm{B} \ }\)にも属さない集合の要素の個数\(\small{ \ n\left(\overline{\mathrm{A}\cup \mathrm{B}}\right) \ }\)も最大になる。
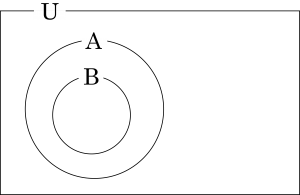
これに対し、二つの部分集合が重ならないとき\(\small{ \ n\left(\mathrm{A}\cap \mathrm{B}\right) \ }\)が最も小さくなる。
このとき、\(\small{ \ \mathrm{A} \ }\)にも\(\small{ \ \mathrm{B} \ }\)にも属さない集合の要素の個数\(\small{ \ n\left(\overline{\mathrm{A}\cup \mathrm{B}}\right) \ }\)も最小になる。

だけど、\(\small{ \ n\left(\mathrm{A}\right) \ }\)、\(\small{ \ n\left(\mathrm{B}\right) \ }\)の数によっては\(\small{ \ n\left(\mathrm{U}\right)\lt n\left(\mathrm{A}\right)+n\left(\mathrm{B}\right) \ }\)になって、\(\small{ \ \mathrm{A} \ }\)にも\(\small{ \ \mathrm{B} \ }\)にも属さない集合の要素の個数\(\small{ \ n\left(\mathrm{A}\cap \mathrm{B}\right) \ }\)が負の値になってしまうよね。
でも負になるのはおかしいから、どちらの部分集合にも属する要素があるからベン図は図のようになるんだ。
このときどちらにも属さない集合の要素の個数\(\small{ \ n\left(\overline{\mathrm{A}\cup \mathrm{B}}\right)=0 \ }\)になるときが、どちらにも属する要素の個数が最小で、どちらにも属さない要素の個数も最小になるんだ。

\(\small{ \ 50 \ }\)人の中で、塾に通っている人は\(\small{ \ 33 \ }\)人、英会話教室に通っている人は\(\small{ \ 27 \ }\)人である。このとき以下の問いについて答えよ。
(1)塾にも英会話教室にも通っていない人は最大何人いるといえるか。
(2)塾と英会話教室どちらにも通っている人は最低何人いるといえるか。
(3)塾だけ通っている人は何人以上何人以下いるといえるか。
(4)英会話教室だけ通っている人は最大何人いるといえるか。
塾に通っている人の集合を\(\small{ \ \mathrm{A} \ }\)、英会話教室に通っている人の集合を\(\small{ \ \mathrm{B} \ }\)とする。
両方に通っている人が最も多くなるのは\(\small{ \ \mathrm{B}\subset \mathrm{A} \ }\)のとき
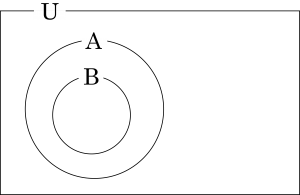
両方に通っている人が最も少なくなるのは\(\small{ \ n(\overline{\mathrm{A}\cup \mathrm{B}})=0 \ }\)のとき

(1)塾にも英会話教室にも通っていない人が最も多いのは\(\small{ \ \mathrm{B}\subset \mathrm{A} \ }\)のとき
\(\small{ \ n(\overline{\mathrm{A}\cup \mathrm{B}})=n(\mathrm{U})-n(\mathrm{A})=17 \ }\)
(2)塾と英会話教室どちらにも通っている人が一番少ないのは\(\small{ \ n(\overline{\mathrm{A}\cup \mathrm{B}})=0 \ }\)のとき
\(\small{\begin{eqnarray} \ n(\mathrm{A}\cap\mathrm{B})&=&n(\mathrm{A})+n(\mathrm{B})-n(\mathrm{U})\\
&=&33+27-50\\
&=&10 \ \end{eqnarray}}\)
(3)塾だけ通っている人は
(i)\(\small{ \ \mathrm{B}\subset \mathrm{A} \ }\)のとき
\(\small{ \ 33-27=6 \ }\)
(ii)\(\small{ \ n(\overline{\mathrm{A}\cup \mathrm{B}})=0 \ }\)のとき
\(\small{ \ 33-10=23 \ }\)
よって\(\small{ \ 6 \ }\)人以上\(\small{ \ 23 \ }\)人以下
(4)英会話だけ通っているひとが一番少ないのは\(\small{ \ n(\overline{\mathrm{A}\cup \mathrm{B}})=0 \ }\)のとき
\(\small{ \ 27-10=17 \ }\)

三つの部分集合の問題
三つの部分集合の問題は連立方程式を作って解く方法がミスをしないから、図のように三つの部分集合の要素の個数を文字でおこう。
そして与えられたヒントから連立方程式を立てて、問題を解こう。
文字の個数と式の数が同じなら連立方程式は解けるからね。

だって集合の記号を使って
なんていちいち書いて計算するの大変だよね。
\(\small{ \ 1 \ }\)から\(\small{ \ 100 \ }\)までの整数のうち、\(\small{ \ 2 \ }\)、\(\small{ \ 5 \ }\)、\(\small{ \ 9 \ }\)の少なくとも一つで割り切れる整数の数を求めよ。
\(\small{ \ 2 \ }\)で割り切れる数の集合を\(\small{ \ \mathrm{A} \ }\)
\(\small{ \ 5 \ }\)で割り切れる数の集合を\(\small{ \ \mathrm{B} \ }\)
\(\small{ \ 9 \ }\)で割り切れる数の集合を\(\small{ \ \mathrm{C} \ }\)
とする。
\(\small{ \ n(\mathrm{A})=50 \ }\)
\(\small{ \ n(\mathrm{B})=20 \ }\)
\(\small{ \ n(\mathrm{C})=11 \ }\)
\(\small{ \ \mathrm{A\cap B} \ }\)は\(\small{ \ 10 \ }\)で割り切れる数
\(\small{ \ \mathrm{A\cap C} \ }\)は\(\small{ \ 18 \ }\)で割り切れる数
\(\small{ \ \mathrm{B\cap C} \ }\)は\(\small{ \ 45 \ }\)で割り切れる数
\(\small{ \ n(\mathrm{A\cap B})=10 \ }\)
\(\small{ \ n(\mathrm{A\cap C})=5 \ }\)
\(\small{ \ n(\mathrm{B\cap C})=2 \ }\)
\(\small{ \ \mathrm{A\cap B\cap C} \ }\)は\(\small{ \ 90 \ }\)で割り切れる数
\(\small{ \ n(\mathrm{A\cap B\cap C})=1 \ }\)
図のように各要素の個数を\(\small{ \ a, \ b, \ c, \ d, \ e, \ f, \ g, \ h \ }\)とすると
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}\\
a+b+c+d+e+f+g+h=100\\
a+b+c+e=50\\
b+c+d+f=20\\
c+e+f+g=11\\
b+c=10\\
c+e=5\\
c+f=2\\
c=1\\
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}\\
a=36\\
b=9\\
c=1\\
d=9\\
e=4\\
f=1\\
g=5\\
h=35
\end{array}
\right.
\end{eqnarray} \ }\)
よって求める答えは\(\small{ \ a+b+c+d+e+f+g=65 \ }\)


Point 集合の要素の個数
①ベン図を利用する
②連立方程式を利用して各部分の集合を求める。

