こんにちは、リンス(@Lins016)です。
今回は余弦定理の証明について学習していこう。
余弦定理
辺の長さや角の大きさを求めるときに利用する余弦定理。
余弦定理がどうやって成り立つのか考えてみよう。
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
a^2=b^2+c^2-2bc\cos \mathrm{A}\\[5pt]
b^2=a^2+c^2-2ac\cos \mathrm{B}\\[5pt]
c^2=a^2+b^2-2ab\cos \mathrm{C}\\[5pt]
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
\cos \mathrm{A}=\displaystyle \frac{b^2+c^2-a^2}{2bc}\\[5pt]
\cos \mathrm{B}=\displaystyle \frac{a^2+c^2-b^2}{2ac}\\[5pt]
\cos \mathrm{C}=\displaystyle \frac{a^2+b^2-c^2}{2ab}\\[5pt]
\end{array}
\right.
\end{eqnarray} \ }\)
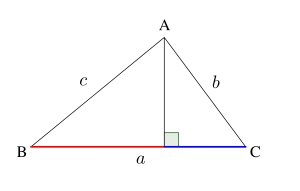
余弦定理の証明(鋭角三角形)
点\(\small{ \ \mathrm{A} \ }\)から辺\(\small{ \ \mathrm{BC} \ }\)に垂線を下ろし、この足を点\(\small{ \ \mathrm{D} \ }\)とする
\(\small{ \ \mathrm{BC}=\mathrm{BD}+\mathrm{CD} \ }\)
\(\small{ \ a=b\cos \mathrm{C}+c\cos\mathrm{B}\cdots① \ }\)
(この式を第一余弦定理という)
同様に残りと点から対辺に垂線を下ろすと
\(\small{ \ b=a\cos \mathrm{C}+c\cos\mathrm{A}\cdots② \ }\)
\(\small{ \ c=a\cos \mathrm{B}+b\cos\mathrm{A}\cdots③ \ }\)
\(\small{ \ -①×a+②×b+③×c\ }\)
\(\small{ \ b^2+c^2-a^2=2bc\cos \mathrm{A} \ }\)
\(\small{ \ ①×a-②×b+③×c\ }\)
\(\small{ \ a^2+c^2-b^2=2ac\cos \mathrm{B} \ }\)
\(\small{ \ ①×a+②×b-③×c\ }\)
\(\small{ \ a^2+b^2-c^2=2ab\cos \mathrm{C} \ }\)
余弦定理の証明(鈍角三角形)
点\(\small{ \ \mathrm{A} \ }\)から直線\(\small{ \ \mathrm{BC} \ }\)に垂線を下ろし、この足を点\(\small{ \ \mathrm{D} \ }\)とすると
\(\small{ \ \mathrm{BC}=\mathrm{BD}-\mathrm{CD} \ }\)
\(\small{ \ a=c\cos \mathrm{B}-b\cos\angle\mathrm{ACD} \ }\)
ここで\(\small{ \ \angle\mathrm{ACD}=180^{\circ}- \angle\mathrm{C}\ }\)より
\(\small{ \ \cos\angle\mathrm{ACD}=\cos(180^{\circ}- \angle\mathrm{C})=-\cos \mathrm{C}\ }\)
\(\small{ \ \therefore a=c\cos \mathrm{B}+b\cos\mathrm{C} \ }\)
よって鈍角三角形のときも\(\small{ \ a=b\cos \mathrm{C}+c\cos\mathrm{B}\cdots① \ }\)は成り立つ
同様に残りと点から対辺に垂線を下ろすと
\(\small{ \ b=a\cos \mathrm{C}+c\cos\mathrm{A}\cdots② \ }\)
\(\small{ \ c=a\cos \mathrm{B}+b\cos\mathrm{A}\cdots③ \ }\)

\(\small{ \ -①×a+②×b+③×c\ }\)
\(\small{ \ b^2+c^2-a^2=2bc\cos \mathrm{A} \ }\)
\(\small{ \ ①×a-②×b+③×c\ }\)
\(\small{ \ a^2+c^2-b^2=2ac\cos \mathrm{B} \ }\)
\(\small{ \ ①×a+②×b-③×c\ }\)
\(\small{ \ a^2+b^2-c^2=2ab\cos \mathrm{C} \ }\)

