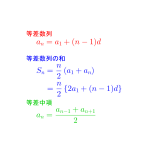こんにちは、リンス(@Lins016)です。
今回は等差数列と階差数列の隣接二項間漸化式について学習していこう。
等差数列と階差数列の漸化式
入試にもよく出題される漸化式だけど、とにかく漸化式の形を覚えよう。
この形ならこの解法っていうのが少なからずあるから、まず最低限の形をおさえておくことが大切なんだ。
その上で応用問題に対応できるように様々な問題の演習をこなしていこう。一気に全部学習するのは大変だから、数回に分けて\(\small{ \ a_{n+1}=pa_n+q \ }\)の形の隣接二項間漸化式を学習していこう。
\(\normalsize{ \ a_{n+1}=pa_n+q \ }\)
①\(\small{ \ p=1 \ }\)、\(\small{ \ q=}\)定数の場合【等差数列】
\(\small{ \ a_{n+1}=a_n+d \ }\)となり、\(\small{a_n=a_1+(n-1)d}\)
②\(\small{ \ p=1 \ }\)、\(\small{ \ q=n \ }\)の式の場合【階差数列】
\(\small{a_{n+1}=a_n+b_n \ }\)となり、\(\small{ \ a_n=a_1+\displaystyle \sum_{ k = 1 }^{ n-1 } b_k \ }\)
今回は\(\small{ \ a_{n+1}=pa_n+q \ }\)の\(\small{ \ p=1 \ }\)のときについての学習になる。
\(\small{ \ a_{n+1}=pa_n+q \ }\)の形のとき、まずは大きく分けて\(\small{ \ p=1、p\neq1 \ }\)、さらに\(\small{ \ q \ }\)が定数か\(\small{ \ n \ }\)の式かに分けて考えていこう。
\(\small{ \ p=1 \ }\)、\(\small{ \ q=}\)定数【等差数列の漸化式】
\(\small{a_{n+1}=a_n+}\)(定数)の式は、第\(\small{ \ n \ }\)項に定数を足すと第\(\small{ \ n+1 \ }\)項になるから、定数\(\small{ \ q \ }\)を公差\(\small{ \ d \ }\)とする等差数列になることがわかるよね。
\(\small{ \ a_{n+1}=a_n+3 \ }\)のような形の漸化式ね。
等差数列といえば\(\small{ \ a_n=a_1+(n-1)d \ }\)になるから、初項と公差を代入して一般項を求めよう。
ちなみに漸化式の問題は必ず初項は与えられてるからね。
\(\small{ \ p=1 \ }\)、\(\small{ \ q=n }\)の式【階差数列の漸化式】
\(\small{a_{n+1}=a_n+(n \ }\)の式)は、(\(\small{ \ n \ }\)の式)\(\small{=b_n \ }\)とおくと、\(\small{b_n=a_{n+1}-a_n \ }\)になるから階差数列って言えるよね。
\(\small{ \ a_{n+1}=a_n+n \ }\)や\(\small{ \ a_{n+1}=a_n+3^n+1 \ }\)のような形の漸化式ね。
階差数列といえば\(\small{ \ a_n=a_1+\displaystyle \sum_{ k = 1 }^{ n-1 } b_k \ }\)になるから、この式に代入して一般項を求めよう。
(1)\(\small{a_1=5,a_{n+1}=a_n-3 \ }\)によって定められる数列\(\small{\{a_n\}}\)の一般項を求めよ。
(2)\(\small{a_1=3,a_{n+1}=a_n+4n+2^n \ }\)によって定められる数列\(\small{\{a_n\}}\)の一般項を求めよ。
(1)\(\small{ \ \{a_n\} \ }\)は初項\(\small{ \ 5 \ }\)、公差\(\small{ \ -3 \ }\)の等差数列だから
\(\small{\begin{eqnarray}a_n&=&5-3(n-1)\\
&=&-3n+8\end{eqnarray}}\)
(2)\(\small{ \ \{a_n\} \ }\)の階差数列\(\small{ \ b_n=4k+2^k \ }\)より
\(\small{ \ n\geqq2 \ }\)のとき
\(\small{\begin{eqnarray}a_n&=&3+\displaystyle \sum_{ k = 1 }^{ n-1 } (4k+2^k)\\
&=&3+4\cdot\displaystyle \frac{1}{2}n(n-1)+\displaystyle \frac{2(2^{n-1}-1)}{2-1}\\
&=&2n^2-2n+2^n+1\end{eqnarray}}\)
これは\(\small{ \ n=1 \ }\)のときも満たす
\(\small{ \ \therefore a_n=2n^2-2n+2^n+1 \ }\)

-

等差数列と等差数列の和
等差数列の一般項とその和や等差中項について詳しく解説しています。
続きを見る
-

階差数列
階差数列の考え方から解き方まで詳しく解説しています。
続きを見る
Point 隣接二項間漸化式\(\small{ \ a_{n+1}=pa_n+q \ }\)
①\(\small{ \ p=1}\)、\(\small{q=}\)定数の場合は、定数を公差とする等差数列
②\(\small{ \ p=1}\)、\(\small{q=n \ }\)の式の場合は、\(\small{q=n \ }\)の式を\(\small{ \ b_n \ }\)とする階差数列
数列\(\small{ \ \{a_n\} \ }\)と\(\small{ \ \{b_n\} \ }\)を
\(\small{ \ a_1=119 \ }\)、\(\small{ \ a_{n+1}-a_n=12n-61(n=1、2、3、\cdots) \ }\)
によって定める。ここで\(\small{ \ c \ }\)は\(\small{ \ 5 \lt c \lt 6 \ }\)を満たす定数とする。以下の問いに答えよ。
(1一般項\(\small{ \ a_n \ }\)と\(\small{ \ b_n \ }\)を求めよ。
(2)\(\small{ \ a_nb_n \gt 0 \ }\)となる\(\small{ \ n \ }\)をすべて求めよ。
(3)\(\small{ \ \displaystyle \sum_{k=1}^{n}a_kb_k \ }\)が最大になる\(\small{ \ n \ }\)を求めよ。
(1)\(\small{ \ a_1=119、a_{n+1}-a_n=12n-61 \ }\)
\(\small{ \ n\geqq2 \ }\)のとき\(\small{ \ a_n=a_1+\displaystyle \sum_{k=1}^{n-1}(12k-61) \ }\)
\(\small{ \ \therefore a_n=6n^2-67n+180 \ }\) これは\(\small{ \ n=1 \ }\)のとき満たす。
次に\(\small{ \ \displaystyle \sum_{k=1}^{n}\displaystyle \frac{1}{b_k}=-\displaystyle \frac{1}{2}n(n-2c+1)\cdots① \ }\)
\(\small{ \ \displaystyle \sum_{k=1}^{n-1}\displaystyle \frac{1}{b_k}=-\displaystyle \frac{1}{2}(n-1)(n-2c) \ }\)
\(\small{ \ n\geqq2 \ }\)のとき辺々引くと
\(\small{ \ \displaystyle \frac{1}{b_n}=\displaystyle \frac{1}{2}\{-(n-2c)-n\}=c-n \ }\)
\(\small{ \ \therefore b_n=\displaystyle \frac{1}{c-n}\cdots② \ }\)
\(\small{ \ ①}\)より\(\small{ \ \displaystyle \frac{1}{b_1}=-\displaystyle \frac{1}{2}\cdot1\cdot(2-2c)=c-1 \ }\)
\(\small{ \ \therefore b_1=\displaystyle \frac{1}{c-1} \ }\)
これは\(\small{ \ n=1 \ }\)のとき\(\small{ \ ②}\)を満たすから
\(\small{ \ \therefore b_n=\displaystyle \frac{1}{c-n} \ }\)
(2)(1)より\(\small{ \ a_nb_n=\displaystyle \frac{6n^2-67n+180}{c-n} \gt 0 \ }\)
\(\small{ \ 5 \lt c \lt 6 \ }\)より\(\small{ \ n\leqq 5 \ }\)のとき\(\small{ \ c \gt n \ }\)
よって\(\small{ \ 6n^2-67n+180 \gt 0 \ }\)
\(\small{ \ (2n-9)(3n-20) \gt 0 \ }\)
\(\small{ \ \therefore n\lt \displaystyle \frac{9}{2}、n\gt\displaystyle \frac{20}{3} \ }\)
\(\small{ \ n\leqq 5 \ }\)より\(\small{ \ n=1、2、3、4 \ }\)
\(\small{ \ n\geqq 6 \ }\)のとき\(\small{ \ c \lt n \ }\)
\(\small{ \ (2n-9)(3n-20) \lt 0 \ }\)
\(\small{ \ \therefore \displaystyle \frac{9}{2} \lt n \lt \displaystyle \frac{20}{3} \ }\)
\(\small{ \ n\geqq 6 \ }\)より\(\small{ \ n=6 \ }\)
よって求める\(\small{ \ n \ }\)は\(\small{ \ n=1、2、3、4、6 \ }\)
(3)
よって\(\small{ \ \displaystyle \sum_{k=1}^{n}a_kb_k \ }\)が最大になる\(\small{ \ n \ }\)の値は
\(\small{ 5 \lt c \lt\displaystyle \frac{60}{11} \ }\)のとき\(\small{ \ n=4 \ }\)
\(\small{ c=\displaystyle \frac{60}{11} \ }\)のとき\(\small{ \ n=4、6 \ }\)
\(\small{ \displaystyle \frac{60}{11} \lt c \lt 6 \ }\)のとき\(\small{ \ n=6 \ }\)

-

数列の和と一般項の関係
こんにちは、リンス(@Lins016)です。 今回は数列の和から一般項を求める方法について学習していこう。 和と一般項の関係 \(\small{ \ \mathrm{S}_n=a_1+a_2+\cdo ...
続きを見る