こんにちは、リンス(@Lins016)です。
今回は三次方程式の解の個数の求め方(定数を含む極値の利用)について学習していこう。
\(\small{ \ x \ }\)の係数に定数を含む三次方程式の解の個数の求め方は極値を利用しよう
今回は「\(\small{ \ x^3-ax-a=0 \ }\)が\(\small{ \ 3 \ }\)つの異なる実数解を持つときの\(\small{ \ a \ }\)の範囲を求めよ」といった定数\(\small{ \ a \ }\)を含んだ解の個数の求め方を学習しよう。
前回の定数分離のものと解き方が違うから注意しよう。
何が違うかっていうと、\(\small{ \ x \ }\)の係数に定数\(\small{ \ a \ }\)がついているってことなんだ。
この形の問題は今回学習する方法で解かないとうまく解けないから、定数分離のように、定数項の部分だけを移行したりしないようにね。
定数項の部分の定数だけ移行しても、\(\small{ \ x \ }\)の係数の定数も移行できないと定数を分離したことにならないからね。
この形の問題は\(\small{ \ x \ }\)の係数に\(\small{ \ a \ }\)がついてるから微分しても\(\small{ \ a \ }\)が残るよね。そこが定数分離の問題と異なるから注意しておこう。
つまり定数を含んだ極大値・極小値と\(\small{ \ x \ }\)軸の関係から解の個数を求めていくんだ。
❶異なる三つの解を持つ場合
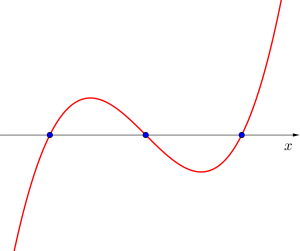
❷異なる実数解を二つ持つ場合
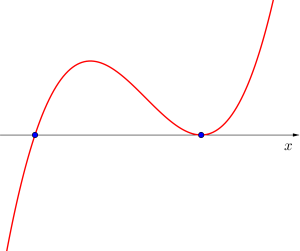
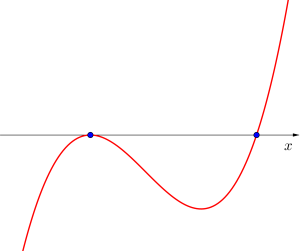
❸異なる実数解を一つ持つ場合
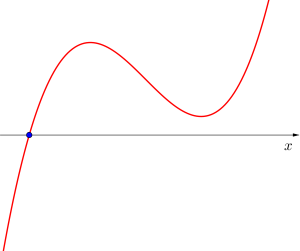
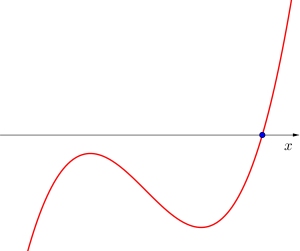
三次関数の極大値×極小値の符号に注目しよう
三次方程式の解の個数の求め方(基本)で学習したように、極大値と極小値の符号によって解をいくつ持つか決まるから、それを利用しよう。
っていっても今回は極大値と極小値にともに定数を含んでいるから、極大値と極小値の符号をひとつずつ考えるより、極大値×極小値の符号を考えよう。
\(\small{ \ f'(x)=0 \ }\)の解には定数が含まれてるから、ひとつずつ考えると解のどっちが大きいかの場合分けも必要になって、かなりめんどくさいよね。でも極大値×極小値を考えることで、どっちが極大でも極小でもいいから、その場合分けも特に必要ないよね。
極大値×極小値が正なら異なる解は一個、\(\small{ \ 0 \ }\)なら異なる解は二個、負なら異なる解は三個になるからね。
三次方程式の解の個数は、1個・2個・3個の計5パターンある
解の個数は定数分離でも、今回のように定数分離しない問題でも解の個数は一個、二個、三個のいずれかになる。
これはグラフから求めるわけだけど、グラフは定数分離なら\(\small{ \ y=a \ }\)と\(\small{ \ y=f(x) \ }\)の位置関係での五通りに、定数分離しない問題でも\(\small{ \ y=f(x,a) \ }\)と\(\small{ \ x \ }\)軸との位置関係の五通りに分かれることが図から分かるよね。
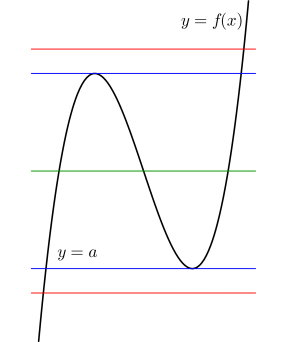
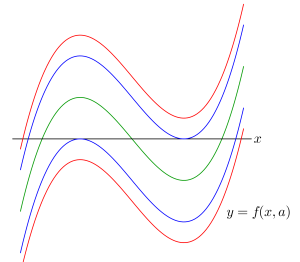
ただ、定数分離しない今回の場合は、極大値×極小値を利用することで\(\small{ \ y=f(x) \ }\)と\(\small{ \ x \ }\)軸との位置関係の五通りを解の個数の三通りにして考えることができるんだ。
ここで注意しておきたいのが、解を二つ以上持つ場合、三次関数のグラフが極値をもたないといけない。極値を持たないグラフだと単調増加や単調減少になるから解は一つしか持たないからね。三次関数が極値を持つ条件も必ず考えよう。
\(\small{ \ x^3+px+4=0 \ }\)が異なる\(\small{ \ 3 \ }\)つの解を持つための定数\(\small{ \ p \ }\)の値の範囲を求めよ。
\(\small{ \ f(x)=x^3+px+4 \ }\)とすると
\(\small{ \ f'(x)=3x^2+p \ }\)
異なる実数解を\(\small{ \ 3 \ }\)つ持つためには\(\small{ \ f(x) \ }\)は極値を持たないといけないので、
\(\small{ \ 3x^2+p=0 \ }\)の判別式\(\small{ \ D=-12p\gt0 \ }\)\(\small{ \ \therefore p \lt 0 \ }\)
\(\small{ \ f'(x)=0 \ }\)とすると
\(\small{ \ x=\pm\sqrt{-\displaystyle \frac{p}{3}} \ }\)
増減表を書くと
\(\small{ \ \begin{array}{c|ccccc}
x & \cdots & -\sqrt{-\displaystyle \frac{p}{3}} & \cdots & \sqrt{-\displaystyle \frac{p}{3}} & \cdots \\
\hline
f’(x) & + & 0 & – & 0 & + \\
\hline
f(x) & \nearrow & f\left(-\sqrt{-\displaystyle \frac{p}{3}}\right) & \searrow & f\left(\sqrt{-\displaystyle \frac{p}{3}}\right) & \nearrow
\end{array} \ }\)
よって\(\small{ \ 3 \ }\)つの解を持つためには
\(\small{ \ f\left(-\sqrt{-\displaystyle \frac{p}{3}}\right)\cdot f\left(\sqrt{-\displaystyle \frac{p}{3}}\right)\lt0 \ }\)
\(\small{ \ \left(-\displaystyle \frac{2p}{3}\sqrt{-\displaystyle \frac{p}{3}}+4\right) \cdot \left(\displaystyle \frac{2p}{3}\sqrt{-\displaystyle \frac{p}{3}}+4\right) \lt 0 \ }\)
\(\small{ \ p^3+108 \lt 0 \ }\)
\(\small{ \ (p+\sqrt[ 3 ]{ 108 })(p^2-\sqrt[ 3 ]{ 108 }p+\sqrt[ 3 ]{ 108^2 }) \lt 0 \ }\)
\(\small{ \ p+\sqrt[ 3 ]{ 108 } \lt 0 \ }\)
\(\small{ \ p \lt -\sqrt[ 3 ]{ 108 }=-3\sqrt[ 3 ]{ 4 } \ }\)

Point
①解を持つ条件を極大値×極小値で確認
②異なる2つ以上の解を持つ場合、極値を持つ条件も忘れない
三次方程式\(\small{ \ x^3-3x^2+3ax+a-2=0 \ }\)が異なる\(\small{ \ 3 \ }\)つの解を持つとき、\(\small{ \ a \ }\)の値の範囲を求めよ。
\(\small{ \ f(x)=x^3-3x^2+3ax+a-2 \ }\)とすると
\(\small{ \ f'(x)=3x^2-6x+3a \ }\)
異なる実数解を\(\small{ \ 3 \ }\)つ持つためには\(\small{ \ f(x) \ }\)は極値を持たないといけないので、
\(\small{ \ 3x^2-6x+3a=0 \ }\)の判別式\(\small{ \ D=36-4\cdot3\cdot3a\gt0 \ }\)より
\(\small{ \ \therefore a \lt 1 \ }\)
\(\small{ \ f'(x)=0 \ }\)とすると
\(\small{ \ x^2-2x+a=0 \ }\)
この2次方程式の解を\(\small{ \ x=\alpha, \ \beta \ }\)とする
\(\small{ \ f(x)=(x^2-2x+a)(x-1)+2(a-1)x+2(a-1) \ }\)より
\(\small{ \ f(\alpha)=2(a-1)\alpha+2(a-1)=2(a-1)(\alpha+1) \ }\)
\(\small{ \ f(\beta)=2(a-1)\beta+2(a-1)=2(a-1)(\beta+1) \ }\)
異なる実数解を\(\small{ \ 3 \ }\)つ持つためには\(\small{ \ f(\alpha)\cdot f(\beta) \lt0 \ }\)であればよい
\(\small{ \ 2(a-1)^2(\alpha+1)(\beta+1)\lt 0 \ }\)
\(\small{ \ \alpha\beta+\alpha+\beta+1 \lt 0 \ }\)
ここで解と係数の関係より
\(\small{ \ \alpha+\beta=2 \ }\)
\(\small{ \ \alpha\beta=a \ }\)
よって\(\small{ \ 2+a+1 \lt 0 \ }\)
\(\small{ \ \therefore a \lt -3 \ }\)

割ることで\(\small{ \ f(x)=f'(x)Q(x)+ax+b \ }\)の形に変形できるよね。
\(\small{ \ f'(x)=0 \ }\)になる値を代入すると、\(\small{ \ f'(x)Q(x) \ }\)の部分は\(\small{ \ 0 \ }\)になるから、結局代入して計算するのは、余りの部分の\(\small{ \ 1 \ }\)次式のところだけでいいからね。
しかも今回のように極大値と極小値の値を両方利用する場合は、代入しなくても解と係数の関係を利用することでより簡単に計算することができるからね。
計算ミスを少しでも減らせるように簡単にできるところはトコトン簡単にするようにしよう。

