こんにちは、リンス(@Lins016)です。
今回はシンプソンの公式の証明について学習していこう。
スポンサーリンク
シンプソンの公式
シンプソンの公式
\(\small{ \ \displaystyle\int_{a}^{b}f(x)dx=\displaystyle\frac{b-a}{6}\left\{f(a)+4f\left(\displaystyle\frac{a+b}{2}\right)+f(b)\right\} \ }\)

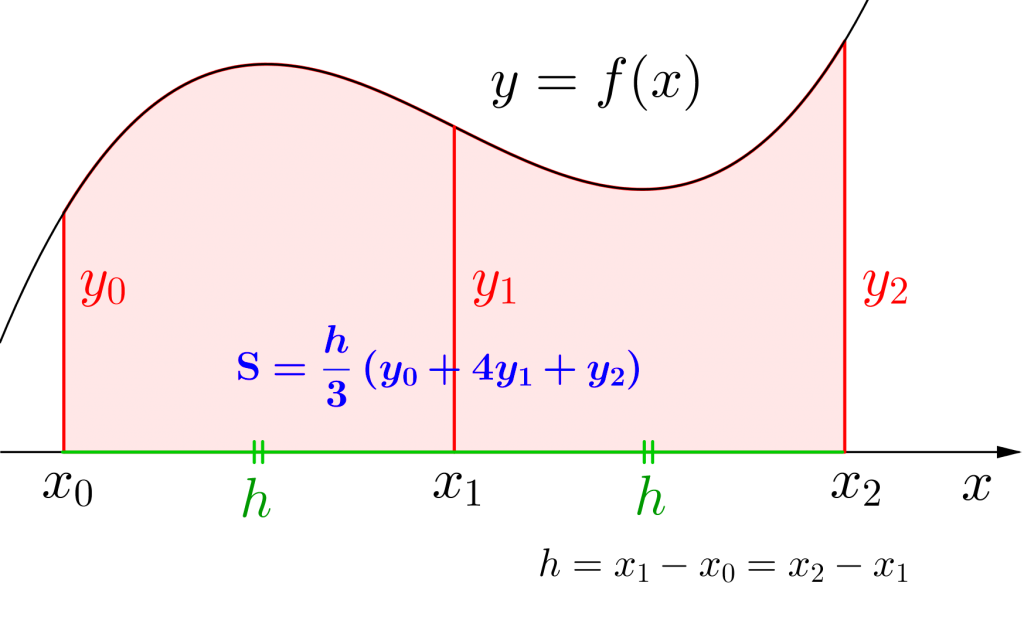
\(\small{ \ \mathrm{S}=\displaystyle\frac{h}{3}(y_0+4y_1+y_2) \ }\)
ただし\(\small{ \ h=\displaystyle\frac{x_2-x_0}{2} \ }\)
シンプソンの公式とは
シンプソンの公式とは
シンプソンの公式(シンプソンのこうしき、Simpson's rule) とは、数値解析の分野において、\(\small{ \ \displaystyle\int_{a}^{b}f(x)dx \ }\)の近似値を得る方法である。
上にもあるように近似値を得る方法だから本当は誤差が生じることになるんだけど、三次以下の多項式関数なら誤差なしで成り立つことが言えるんだ。
シンプソンの公式の証明
\(\small{ \ f(x)=Ax^3+Bx^2+Cx+D \ }\)とする。
\(\small{ \ \displaystyle\int_{a}^{b}f(x)dx\\
=\displaystyle\int_{a}^{b}(Ax^3+Bx^2+Cx+D)dx\\
=\left[\displaystyle \frac{1}{4}Ax^4+\displaystyle \frac{1}{3}Bx^3+\displaystyle \frac{1}{2}Cx+dx\right]_{a}^{b}\\
=\displaystyle \frac{1}{12}\left[3Ax^4+4Bx^3+6Cx+12Dx\right]_{a}^{b}\\
=\displaystyle \frac{1}{12}\left\{3A\left(b^4-a^4\right)+4B\left(b^3-a^3\right)+6C\left(b^2-a^2\right)+12D\left(b-a\right)\right\}\\
=\displaystyle \frac{b-a}{12}\left\{3A\left(a+b\right)\left(a^2+b^2\right)+4B\left(a^2+ab+b^2\right)+6C\left(a+b\right)+12D\right\}\\
=\displaystyle \frac{b-a}{6}\left\{\displaystyle \frac{3}{2}A\left(a+b\right)\left(a^2+b^2\right)+2B\left(a^2+ab+b^2\right)+3C\left(a+b\right)+6D\right\} \ }\)
=\displaystyle\int_{a}^{b}(Ax^3+Bx^2+Cx+D)dx\\
=\left[\displaystyle \frac{1}{4}Ax^4+\displaystyle \frac{1}{3}Bx^3+\displaystyle \frac{1}{2}Cx+dx\right]_{a}^{b}\\
=\displaystyle \frac{1}{12}\left[3Ax^4+4Bx^3+6Cx+12Dx\right]_{a}^{b}\\
=\displaystyle \frac{1}{12}\left\{3A\left(b^4-a^4\right)+4B\left(b^3-a^3\right)+6C\left(b^2-a^2\right)+12D\left(b-a\right)\right\}\\
=\displaystyle \frac{b-a}{12}\left\{3A\left(a+b\right)\left(a^2+b^2\right)+4B\left(a^2+ab+b^2\right)+6C\left(a+b\right)+12D\right\}\\
=\displaystyle \frac{b-a}{6}\left\{\displaystyle \frac{3}{2}A\left(a+b\right)\left(a^2+b^2\right)+2B\left(a^2+ab+b^2\right)+3C\left(a+b\right)+6D\right\} \ }\)
\(\small{ \ f(a)=Aa^3+Ba^2+Ca+D \ }\)
\(\small{ \ f(b)=Ab^3+Bb^2+Cb+D \ }\)
\(\small{ \ f\left(\displaystyle \frac{a+b}{2}\right)=A\left(\displaystyle \frac{a+b}{2}\right)^3+B\left(\displaystyle \frac{a+b}{2}\right)^2+C\left(\displaystyle \frac{a+b}{2}\right)+D \ }\)
\(\small{ \ 4f\left(\displaystyle \frac{a+b}{2}\right)=A\cdot\displaystyle \frac{(a+b)^3}{2}+B(a+b)^2+2C(a+b)+4D \ }\)
\(\small{ \ f(a)+4f\left(\displaystyle \frac{a+b}{2}\right)+f(b)\\
=A\left\{a^3+b^3+\displaystyle\frac{1}{2}(a+b)^2\right\}+B\left\{a^2+b^2+(a+b)^2\right\}+C\left\{a+b+2(a+b)\right\}+6D\\
=\displaystyle\frac{3}{2}A(a^3+b^3+a^2b+ab^2)+2B\left(a^2+ab+b^2\right)+3C\left(a+b\right)+6D\\
=\displaystyle\frac{3}{2}A(a+b)(a^2+b^2)+2B\left(a^2+ab+b^2\right)+3C\left(a+b\right)+6D}\)
=A\left\{a^3+b^3+\displaystyle\frac{1}{2}(a+b)^2\right\}+B\left\{a^2+b^2+(a+b)^2\right\}+C\left\{a+b+2(a+b)\right\}+6D\\
=\displaystyle\frac{3}{2}A(a^3+b^3+a^2b+ab^2)+2B\left(a^2+ab+b^2\right)+3C\left(a+b\right)+6D\\
=\displaystyle\frac{3}{2}A(a+b)(a^2+b^2)+2B\left(a^2+ab+b^2\right)+3C\left(a+b\right)+6D}\)
\(\small{ \ \therefore \displaystyle\int_{a}^{b}f(x)dx=\displaystyle\frac{b-a}{6}\left\{f(a)+4f\left(\displaystyle\frac{a+b}{2}\right)+f(b)\right\} \ }\)

特に三次関数の定積分を計算するとき、\(\small{ \ a, \ b \ }\)の偶奇が一致していると計算が非常に楽になるから検算用に覚えておくといいからね。
またこの式の文字を変換した
\(\small{ \ \mathrm{S}=\displaystyle\frac{h}{3}(y_0+4y_1+y_2) \ }\)
(ただし\(\small{ \ h=\displaystyle\frac{x_2-x_0}{2} \ }\))
も参考書等に取り上げられているけど、同じ意味になるからね。

