こんにちは、リンス(@Lins016)です。
今回は三角関数の極限の証明を学習していこう。
三角関数の極限の証明
面積を利用した三角関数の極限の証明方法
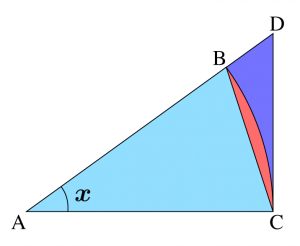
\(\small{ \ \mathrm{AB=AC}=1、\angle \mathrm{ACD}= \displaystyle \frac{\pi}{2} \ }\)とすると
三角形\(\small{ \ \mathrm{ABC} \ }\)の面積
\(\small{ \ S_1=\displaystyle \frac{1}{2}\cdot1\cdot1\cdot \sin x=\displaystyle \frac{1}{2}\sin x \ }\)
おうぎ形\(\small{ \ \mathrm{ABC} \ }\)の面積
\(\small{ \ S_2=\displaystyle \frac{1}{2}\cdot1^2\cdot x=\displaystyle \frac{1}{2}x \ }\)
三角形\(\small{ \ \mathrm{ACD} \ }\)の面積
\(\small{ \ S_3=\displaystyle \frac{1}{2}\cdot1\cdot\tan x=\displaystyle \frac{1}{2}\tan x \ }\)
図より\(\small{ \ S_1 \lt S_2 \lt S_3 \ }\)
\(\small{ \ \displaystyle \frac{1}{2}\sin x \lt \displaystyle \frac{1}{2}x \lt \displaystyle \frac{1}{2}\tan x \ }\)
\(\small{ \ \sin x \lt x \lt \tan x \ }\)
\(\small{ \ \sin x \gt 0 \ }\)より逆数をとると
\(\small{ \ \displaystyle \frac{\cos x}{\sin x} \lt \displaystyle \frac{1}{x} \lt \displaystyle \frac{1}{\sin x}\ }\)
\(\small{ \ \sin x \ }\)をかけて
\(\small{ \ \cos x \lt \displaystyle \frac{\sin x}{x} \lt 1 \ }\)
\(\small{ \ \displaystyle \lim_{ x \to 0 } \cos x =1 \ }\)からはさみうちの原理より
\(\small{ \ \displaystyle \lim_{ x \to 0 }\displaystyle \frac{\sin x}{x} =1 \ }\)