加法定理の証明

2016年11月11日

こんにちは、リンス(@Lins016)です。
今回は加法定理の証明について学習していこう。

加法定理

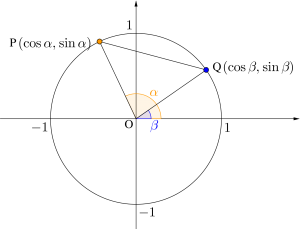
三角関数で一番重要な加法定理の証明は、以前東京大学の入試にも出題されたこともある。単位円を利用して考えてみよう。

加法定理

sin (α + β) = sin α cos β + cos α sin β

$\small{ \ \sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta \ }$

sin (α - β) = sin α cos β - cos α sin β

$\small{ \ \sin(\alpha-\beta)=\sin \alpha \cos \beta-\cos\alpha \sin \beta \ }$

cos (α + β) = cos α cos β - sin α sin β

$\small{ \ \cos(\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta \ }$

cos (α - β) = cos α cos β + sin α sin β

$\small{ \ \cos(\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta \ }$

tan (α + β) = \frac{tan α + tan β}{1 - tan α tan β}

$\small{ \ \tan(\alpha+\beta)=\displaystyle \frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta} \ }$

tan (α - β) = \frac{tan α - tan β}{1 + tan α tan β}

$\small{ \ \tan(\alpha-\beta)=\displaystyle \frac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta} \ }$

加法定理の証明

三平方の定理より
$\small{ \ \mathrm{PQ}^2=(\cos\alpha-\cos\beta)^2+(\sin\alpha-\sin\beta)^2 \ }$

単位円より $\small{ \ \mathrm{OP}=\mathrm{OQ}=1 \ }$
$\small{ \ \mathrm{OP}^2+ \mathrm{OQ}^2-2\mathrm{OP}\cdot\mathrm{OQ}\cos (\alpha-\beta) \ }$
$\small{ \ =1^2+1^2-2\cdot1\cdot1 \cos(\alpha-\beta) \ }$

余弦定理より
$\small{ \ \mathrm{PQ}^2=\mathrm{OP}^2+ \mathrm{OQ}^2-2\mathrm{OP}\cdot\mathrm{OQ}\cos (\alpha-\beta) \ }$

よって $\small{ \ 2-\cos \alpha \cos \beta-2\sin \alpha \sin\beta=2-\cos(\alpha-\beta) \ }$
$\small{ \ \therefore \cos(\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\cdots① \ }$

$\small{ \ \cos(\alpha-(-\beta) )=\cos \alpha \cos(-\beta)+\sin \alpha \sin (-\beta) \ }$
$\small{ \ \therefore \cos(\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta\cdots② \ }$

$\small{ \ \cos\left(90^{\circ}-\theta\right)=\sin\theta \ }$ より
$\small{ \ \cos(90^{\circ}-\alpha-\beta)=\sin(\alpha+\beta) \ }$
$\small{ ①}$ より

cos (90^{\circ} - α - β) = cos (90^{\circ} - α) cos β + sin (90^{\circ} - α) cos β

$\small{ \ \cos(90^{\circ}-\alpha-\beta)=\cos(90^{\circ}-\alpha)\cos\beta+\sin(90^{\circ}-\alpha)\cos\beta \ }$

$\small{ \ \cos(90^{\circ}-\alpha)=\sin\alpha \ }$
$\small{ \ \sin(90^{\circ}-\alpha)=\cos\alpha \ }$
よって
$\small{ \ \sin(\alpha+\beta) =\sin \alpha \cos\beta+ \cos \alpha \sin \beta\cdots③ \ }$

$\small{ \ \sin(\alpha-\beta) =\sin \alpha \cos(-\beta)+ \cos \alpha \sin(-\beta) \ }$
$\small{ \ \sin(-\theta)=-\sin\theta \ }$ より
$\small{ \ \therefore \sin(\alpha-\beta) =\sin \alpha \cos\beta- \cos \alpha \sin\beta\cdots④ \ }$

tan (α + β) = \frac{sin (α + β)}{cos (α + β)} = \frac{sin α cos β + cos α sin β}{cos α cos β - sin α sin β}

$\small{ \ \tan(\alpha+\beta)=\displaystyle \frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}=\displaystyle \frac{\sin \alpha \cos\beta+ \cos \alpha \sin \beta}{\cos \alpha \cos \beta-\sin \alpha \sin \beta} \ }$

右辺の分子と分母にそれぞれ $\small{ \ \displaystyle \frac{1}{\cos \alpha \cos \beta} \ }$ をかけると
$\small{ \ \tan(\alpha+\beta)=\displaystyle \frac{\displaystyle \frac{\sin \alpha \cos\beta+ \cos \alpha \sin \beta}{\cos \alpha \cos \beta}}{\displaystyle \frac{\cos \alpha \cos \beta-\sin \alpha \sin \beta}{\cos \alpha \cos \beta}} \ }$
これを整理すると
$\small{ \ \tan(\alpha+\beta)=\displaystyle \frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\cdots⑤ \ }$

$\small{ \ \tan(\alpha-\beta)=\displaystyle \frac{\tan\alpha+(-\tan\beta)}{1-\tan\alpha(-\tan\beta)} \ }$
$\small{ \ \tan(-\theta)=-\tan\theta \ }$ より
$\small{ \ \therefore \tan(\alpha-\beta)=\displaystyle \frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\cdots⑥ \ }$