こんにちは、リンス(@Lins016)です。
今回は条件付き確率について学習していこう。
条件付き確率
条件付き確率は名前の通り、「条件の付いた確率」のこと。
条件って言うとなんか難しい感じがするけど、そんなことなくて「事象\(\small{ \ A \ }\)が起こるとき事象\(\small{ \ B \ }\)が起こる確率\(\small{ \ P_A(B) \ }\)」の場合、「事象\(\small{ \ A \ }\)が起こるとき」っていうのが条件になる。
今回は条件付き確率の理解と、どんな問題文が条件付き確率になっているのかなど、条件付き確率の基本事項をおさえていこう。
\(\small{ \ P_A(B)=\displaystyle\frac{P(A\cap B)}{P(A)} \ }\)
\(\small{ \ P_A(B)=\displaystyle\frac{n(A\cap B)}{n(A)} \ }\)
条件付き確率の試行と事象
一般に\(\small{ \ 1 \ }\)つの試行における\(\small{ \ 2 \ }\)つの事象\(\small{ \ A \ }\)と\(\small{ \ B \ }\)について、事象\(\small{ \ A \ }\)が起こったとして、そのときに事象\(\small{ \ B \ }\)が起こる確率を、\(\small{ \ A \ }\)が起こったときの\(\small{ \ B \ }\)が起こる条件付き確率というんだ。この確率を記号で\(\small{ \ P_A(B) \ }\)って書く。
この\(\small{ \ 1 \ }\)つの試行ってことが大切で、独立した試行が\(\small{ \ 2 \ }\)つあると、それぞれの結果の事象は独立になるから、条件付き確率の問題にならないんだ。
確率の試行と事象については、下の記事を読んで確認しておこう。 試行と事象の違いや排反、独立について詳しく解説しています。 続きを見る

確率における独立
「事象\(\small{ \ A \ }\)が起こるときの事象\(\small{ \ B \ }\)が起こる確率」が条件付き確率で、これは事象\(\small{ \ A \ }\)が起こる場合を全事象としたとき、事象\(\small{ \ B \ }\)の起こる確率だから、\(\small{ \ P_A(B)= \displaystyle\frac{n(A \cap B)}{n(A)} \ }\)になる。
これを全事象\(\small{ \ n(U) \ }\)で割ると\(\small{ \ P_A(B)=\displaystyle\frac{\displaystyle\frac{n(A\cap B)}{n(U)}}{\displaystyle\frac{n(A)}{n(U)}}= \displaystyle\frac{P(A\cap B)}{P(A)} \ }\)ってなるから、「事象\(\small{ \ A \ }\)と事象\(\small{ \ B \ }\)が同時に起こる確率\(\small{ \ P(A\cap B) \ }\)」を「事象\(\small{ \ A \ }\)が起こる確率\(\small{ \ P(A) \ }\)」で割ればいいんだ。これが\(\small{ \ A \ }\)が起こったときの\(\small{ \ B \ }\)が起こる条件付き確率の値になる。
勘違いしやすい問題文
条件付き確率の計算方法がわかったけど、これだけじゃだめなんだ。どの問題が条件付き確率なのかわからないといけない。だって問題文には「条件付き確率を求めよ。」とは書いていない。条件付き確率の問題も普通の確率の問題と同じ様に「〜である確率を求めよ。」って書いてあるんだ。だから問題文を読んでこの問題は条件付き確率の問題だって自分で判断する必要がある。
条件付き確率の問題文を「〇〇〇のとき、△△△である確率」って覚えている人も多いと思う。それじゃ次の\(\small{ \ 2 \ }\)つの問題を見てみよう。
当たりくじ\(\small{ \ 4 \ }\)本を含む\(\small{ \ 20 \ }\)本のくじがある。引いたくじはもとに戻さないものとして、\(\small{ \ \mathrm{A} \ }\)、\(\small{ \ \mathrm{B} \ }\)の\(\small{ \ 2 \ }\)人がこの順に1本ずつくじを引く。
(1)\(\small{ \ \mathrm{A} \ }\)が当たりを引いたとき、\(\small{ \ \mathrm{B} \ }\)が当たりを引く確率を求めよ。
(2)\(\small{ \ \mathrm{A} \ }\)、\(\small{ \ \mathrm{B} \ }\)の後に\(\small{ \ \mathrm{C} \ }\)がくじを引いたとき、はずれる確率を求めよ。
(1)も(2)も「〇〇〇のとき、△△△である確率」の形になっているよね。でもきちんと確認すると(1)の〇〇〇のとき、は「\(\small{ \ \mathrm{A} \ }\)が当たりを引いたとき」って事象を表しているよね。それに対して(2)は「\(\small{ \ \mathrm{C} \ }\)がくじを引いたとき」って試行を表している。
条件付き確率の「〇〇〇のとき」は事象を表すから、(1)は条件付き確率の問題、(2)は単純な確率の問題になるんだ。
きちんと理解している人には大したことない問題かもしれないけど、大切なことだから、上にあるリンク先の記事「確率における独立」を読んでいない人は一度読んで試行と事象について確認しておこう。
血液型が\(\small{ \ \mathrm{A} \ }\)型、\(\small{ \ \mathrm{B} \ }\)型である\(\small{ \ 100 \ }\)人を調べると、男子\(\small{ \ 60 \ }\)人、女子\(\small{ \ 40 \ }\)人で、\(\small{ \ \mathrm{A} \ }\)型は男子\(\small{ \ 35 \ }\)人、女子\(\small{ \ 14 \ }\)人であった。次の確率を求めよ。
(1) 選ばれた\(\small{ \ 1 \ }\)人が女子のとき、その人が\(\small{ \ \mathrm{A} \ }\)型である確率
(2) 選ばれた\(\small{ \ 1 \ }\)人が\(\small{ \ \mathrm{B} \ }\)型のとき、その人が男子である確率
女子である事象を\(\small{ \ E \ }\)、血液型が\(\small{ \ \mathrm{A} \ }\)型である事象を\(\small{ \ F \ }\)とする。
(1)求める確率は
\(\small{ \ P_E(F)= \displaystyle\frac{P(E\cap F)}{P(E)}=\displaystyle\frac{\displaystyle\frac{14}{100}}{\displaystyle\frac{40}{100}}=\displaystyle\frac{7}{20} \ }\)
(2)求める確率は
\(\small{ \ P_{\overline{F}}(\overline{E})=\displaystyle\frac{P(\overline{F}\cap \overline{E})}{P(\overline{F})}=\displaystyle\frac{\displaystyle\frac{25}{100}}{\displaystyle\frac{51}{100}}=\displaystyle\frac{25}{51} \ }\)
条件付き確率とベン図とカルノー図
条件付き確率を考えるとき視覚的にベン図やカルノー図を利用することで確率がわかりやすくなる。これについては下の記事を確認しておこう。 ベン図とカルノー図の違いやカルノー図の簡単な使い方について詳しく解説しています。 続きを見る

カルノー図
さっきの例題をカルノー図で書くと次のようになる。与えられた情報は黒字の部分だけど、黒字の部分から赤字の部分もすぐに調べることができるよね。こうなると問題はあっさり解ける。
男子\(\small{ \ 60 \ }\)人、女子\(\small{ \ 40 \ }\)人の合計\(\small{ \ 100 \ }\)人
\(\small{\mathrm{A} \ }\)型は男子\(\small{ \ 35 \ }\)人、女子\(\small{ \ 14 \ }\)人
女子が選ばれる事象を\(\small{ \ E \ }\)
血液型が\(\small{ \ \mathrm{A} \ }\)型である事象を\(\small{ \ F \ }\)
としてカルノー図をかくと
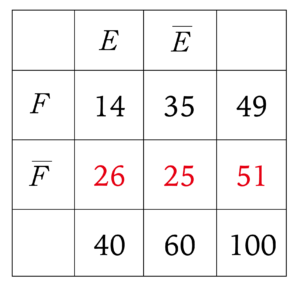
上のカルノー図は確率じゃなくて要素の個数を書いたけど、欄に確率を記入する場合は、次のように書けるから覚えておこう。
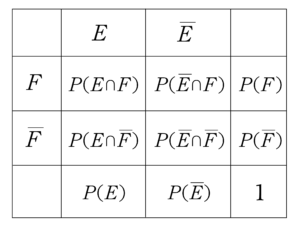
Point 条件付き確率
①条件付き確率の計算式\(\small{ \ P_E(F)= \displaystyle\frac{P(E\cap F)}{P(E)} \ }\)を覚える。
②問題が条件付き確率の問題か判断できるようにする。
③カルノー図を書ける様にする。
胎児の性別を判定するための検査法がある。この検査法は、
・産まれてくる子どもの性別が男の場合、男と判定する確率が\(\small{ \ \displaystyle\frac{17}{20} \ }\)
・産まれてくる子どもの性別が女の場合、女と判定する確率が\(\small{ \ \displaystyle\frac{3}{4} \ }\)
・検査結果は、男か女かのいずれか
であるとする。以下の問いに答えよ。ただし、産まれてくる子どもの性別が男である確率と女である確率は等しいとする。
(1)産まれてくる子どもの性別が女であるとき、誤って男と判定される確率を求めよ。
(2)検査結果が男である確率を求めよ。
(3)検査結果が男である場合と女である場合とでは、どちらがより高い確率で正しいか答えよ。
(1)産まれてくる子どもの性別が女であるとき、女と判定する確率が\(\small{ \ \displaystyle\frac{3}{4} \ }\)であるから、誤って男と判定される確率は、
\(\small{ \ 1-\displaystyle\frac{3}{4}=\displaystyle\frac{1}{4} \ }\)
(2)検査結果が男であるのは、次の場合である。
(i)産まれてくる子ともの性別が男であり、検査結果が男である場合。
(ii)産まれてくる子どもの性別が女であり、検査結果が男である場合。
よって、求める確率は
\(\small{ \ \displaystyle\frac{1}{2}\times\displaystyle\frac{17}{20}+\displaystyle\frac{1}{2}\times\displaystyle\frac{1}{4}=\displaystyle\frac{11}{20} \ }\)
(3)検査結果が男であるとき、産まれてくる子どもの性別が男である条件付き確率は、(2)より、
\(\small{ \ \displaystyle\frac{\displaystyle\frac{1}{2}\times\displaystyle\frac{17}{20}}{\displaystyle\frac{11}{20}}=\displaystyle\frac{17}{22}\cdots① \ }\)
また、検査結果が女である確率は、(2)と同様に考えて、
\(\small{ \ \displaystyle\frac{1}{2}\times\left(1-\displaystyle\frac{17}{20}\right)+\displaystyle\frac{1}{2}\times\displaystyle\frac{3}{4}=\displaystyle\frac{9}{20} \ }\)
であるから、検査結果が女であるとき、産まれてくる子どもの性別が女である条件付き確率は
\(\small{ \ \displaystyle\frac{\displaystyle\frac{1}{2}\times\displaystyle\frac{3}{4}}{\displaystyle\frac{9}{20}}=\displaystyle\frac{5}{6}\cdots② \ }\)
①、②より、検査結果が女である場合の方が男である場合より高い確率で正しい。
産まれてくる子どもの性別が男である事象を\(\small{ \ E \ }\)、検査結果が男である事象を\(\small{ \ F \ }\)として、カルノー図を書くと次のようになる。
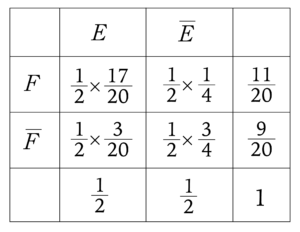
(1)産まれてくる子どもの性別が女であるとき、誤って男と判定される確率は、
\(\small{ \ P_{\overline{E}}(F)=\displaystyle\frac{P(\overline{E}\cap F)}{P(\overline{E})}=\displaystyle\frac{\displaystyle\frac{1}{2}\times\displaystyle\frac{1}{4}}{\displaystyle\frac{1}{2}}=\displaystyle\frac{1}{4} \ }\)
(2)検査結果が男である確率は
\(\small{ \ P(F)=\displaystyle\frac{11}{20} \ }\)
(3)検査結果が男であるとき、産まれてくる子どもの性別が男である条件付き確率は
\(\small{ \ P_F(E)=\displaystyle\frac{P(E\cap F)}{P(F)}=\displaystyle\frac{\displaystyle\frac{1}{2}\times\displaystyle\frac{17}{20}}{\displaystyle\frac{11}{20}}=\displaystyle\frac{17}{22} \ }\)
検査結果が女であるとき、産まれてくる子どもの性別が女である条件付き確率は
\(\small{ \ P_\overline{F}(\overline{E})=\displaystyle\frac{P(\overline{E}\cap \overline{F})}{P(\overline{F})}=\displaystyle\frac{\displaystyle\frac{1}{2}\times\displaystyle\frac{3}{4}}{\displaystyle\frac{9}{20}}=\displaystyle\frac{5}{6} \ }\)
よって、検査結果が女である場合の方が男である場合より高い確率で正しい。

カルノー図がなくても解けるけど、視覚的に考えやすくなるし、計算もしやすい。カルノー図が書けた時点で大体の計算が終わってるからね。色々な条件付き確率の問題にカルノー図を取り入れてみよう。

