こんにちは、リンス(@Lins016)です。今回は確率の基本性質について学習していこう。
確率の基本性質
確率の問題を解く上で重要になる積事象、和事象、余事象、排反についてきちんと理解して、確率の計算を確実にできるようにしよう。
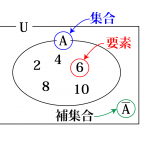
ある試行における全事象を\(\small{ \ \mathrm{U} \ }\)、空事象を\(\small{ \ \varnothing \ }\)、事象を\(\small{ \ \mathrm{A}、\mathrm{B} \ }\)とするとき
積事象
「事象\(\small{ \ \mathrm{A} \ }\)と事象\(\small{ \ \mathrm{B} \ }\)がともに起こる」事象のことで\(\small{ \ \mathrm{A}\cap \mathrm{B} \ }\)で表す
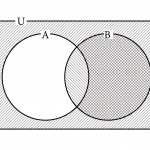
和事象
「事象\(\small{ \ \mathrm{A} \ }\)または事象\(\small{ \ \mathrm{B} \ }\)が起こる」事象のことで\(\small{ \ \mathrm{A}\cup \mathrm{B} \ }\)で表す
排反
「事象\(\small{ \ \mathrm{A} \ }\)と事象\(\small{ \ \mathrm{B} \ }\)が決して同時に起こらないとき」事象\(\small{ \ \mathrm{A} \ }\)と事象\(\small{ \ \mathrm{B} \ }\)は互いに排反であるという\(\small{ \ \mathrm{A}\cap \mathrm{B}=\varnothing \ }\)
和事象の確率
\(\small{ \ P(\mathrm{A}\cup \mathrm{B})= P(\mathrm{A})+P(\mathrm{B})-P(\mathrm{A}\cap \mathrm{B}) \ }\)
ただし、事象\(\small{ \ \mathrm{A} \ }\)と事象\(\small{ \ \mathrm{B} \ }\)は互いに排反のとき\(\small{ \ P(\mathrm{A}\cup \mathrm{B})=P(\mathrm{A})+P(\mathrm{B}) \ }\)
余事象の確率
\(\small{ \ P(\mathrm{A})=1-P(\overline{\mathrm{A}}) \ }\)
積事象と和事象の確率
\(\small{ \ 1 \ }\)つの事象\(\small{ \ \mathrm{A} \ }\)の確率を求めるのは\(\small{ \ \displaystyle\frac{n(\mathrm{A})}{n(\mathrm{U})} \ }\)の値を求めれば良かったよね。
でも\(\small{ \ 2 \ }\)つの事象があるとき、求める確率は複数あるんだ。その中で大切なのが積事象の確率と和事象の確率。
積事象っていうのは「\(\small{ \ 2 \ }\)つの事象がともに起こる」こと。\(\small{ \ 2 \ }\)つの事象を事象\(\small{ \ \mathrm{A} \ }\)が事象\(\small{ \ \mathrm{B} \ }\)とすると、\(\small{ \ \mathrm{A}\cap \mathrm{B} \ }\)で表される。
これに対し、和事象っていうのは「\(\small{ \ 2 \ }\)つの事象の少なくとも一方が起こる」こと。\(\small{ \ \mathrm{A}\cup \mathrm{B} \ }\)で表される。これらの確率を具体的に見てみよう。
\(\small{ \ 1 \ }\)個のサイコロを投げるとき、事象\(\small{ \ \mathrm{A} \ }\):偶数の目が出る事象\(\small{ \ \mathrm{B} \ }\):\(\small{ \ 3 \ }\)の倍数が出るとすると、事象\(\small{ \ \mathrm{A} \ }\)は\(\small{ \ 2, \ 4, \ 6 \ }\)のいずれかの目が出ることで、事象\(\small{ \ \mathrm{B} \ }\)は\(\small{ \ 3, \ 6 \ }\)のいずれかの目が出ることになる。
\(\small{ \ \mathrm{A}\cap \mathrm{B} \ }\)は\(\small{ \ 6 \ }\)の目が出ることになるし、\(\small{ \ \mathrm{A}\cup \mathrm{B} \ }\)は\(\small{ \ 2, \ 3, \ 4, \ 6 \ }\)の目が出ることになる。
だから積事象の確率\(\small{ \ P\left(\mathrm{A}\cap \mathrm{B}\right)=\displaystyle\frac{1}{6} \ }\)で、和事象の確率\(\small{ \ P\left(\mathrm{A}\cup \mathrm{B}\right)=\displaystyle\frac{4}{6}=\displaystyle\frac{2}{3} \ }\)になる。
積事象・和事象については集合やベン図を利用することもあるから復習しておこう。
-

集合の要素の個数
ベン図や連立方程式の利用など様々な問題について詳しく解説しています。
続きを見る
-

ベン図の書き方
和集合や共通部分のベン図を利用した考え方について詳しく解説しています。
続きを見る
排反の事象の確率
\(\small{ \ 2 \ }\)つの事象を事象\(\small{ \ \mathrm{A} \ }\)が事象\(\small{ \ \mathrm{B} \ }\)が同時に起こることがないとき、この\(\small{ \ 2 \ }\)つの事象は互いに排反であるっていう。
例えば、\(\small{ \ 1 \ }\)個のサイコロを投げるとき、事象\(\small{ \ \mathrm{A} \ }\):偶数の目が出る事象、\(\small{ \ \mathrm{B} \ }\):奇数の目が出るとすると、\(\small{ \ 2 \ }\)つの事象は同時に起こることはないよね、
つまり\(\small{ \ \mathrm{A}\cap \mathrm{B}=\varnothing \ }\)だよね。だからこの\(\small{ \ 2 \ }\)つの事象は排反ってことになるんだ。
次に別な例で考えてみよう。
赤玉\(\small{ \ 4 \ }\)個、白玉\(\small{ \ 3 \ }\)個の合計\(\small{ \ 7 \ }\)個の球が入っている袋から玉を\(\small{ \ 4 \ }\)個取り出すとき、赤玉を\(\small{ \ 3 \ }\)個以上取り出す確率を考えてみよう。
赤玉\(\small{ \ 3 \ }\)個以上っていうのは「赤玉\(\small{ \ 3 \ }\)個と白玉\(\small{ \ 1 \ }\)個取り出すとき」(事象\(\small{ \ \mathrm{A} \ }\))と、「赤玉\(\small{ \ 4 \ }\)個、白玉\(\small{ \ 0 \ }\)個取り出す」(事象\(\small{ \ \mathrm{B} \ }\))ときになる。
この\(\small{ \ 2 \ }\)つの事象は同時に起こることはないから排反になるんだ。
事象\(\small{ \ \mathrm{A} \ }\)の確率は\(\small{ \ P(\mathrm{A})=\displaystyle\frac{{}_4\mathrm{C}_3\cdot{}_3\mathrm{C}_1}{{}_7\mathrm{C}_4}=\displaystyle\frac{12}{35} \ }\)
事象\(\small{ \ \mathrm{B} \ }\)の確率は\(\small{ \ P(\mathrm{B})=\displaystyle\frac{{}_4\mathrm{C}_4}{{}_7\mathrm{C}_4}=\displaystyle\frac{1}{35} \ }\)
これらは排反だから求める赤玉を\(\small{ \ 3 \ }\)個以上取り出す確率は\(\small{ \ P(\mathrm{A})+P(\mathrm{B})=\displaystyle\frac{13}{35} \ }\)になるんだ。
排反の事象の確率は掛け算することはないから注意しよう。上の計算みたいに足し算になる場合がほとんどだからね。よく排反の確率を掛けて失敗してる生徒見かけるからね。

余事象を利用した確率
事象\(\small{ \ \mathrm{A} \ }\)に対して、「事象\(\small{ \ \mathrm{A} \ }\)が起こらない」ことを「\(\small{ \ \mathrm{A} \ }\)の余事象」っていうんだ。
この余事象を利用することで確率がより簡単に求められるときがあるんだ。例えば、赤玉\(\small{ \ 4 \ }\)個、白玉\(\small{ \ 5 \ }\)個の合計\(\small{ \ 9 \ }\)個の球が入っている袋から玉を\(\small{ \ 4 \ }\)個取り出すとき、赤玉を\(\small{ \ 2 \ }\)個以上取り出す確率を考えてみよう。
赤玉\(\small{ \ k \ }\)個とり出す確率を\(\small{ \ P_k \ }\)とすると、赤玉を\(\small{ \ 2 \ }\)個以上取り出す確率は\(\small{ \ P_2+P_3+P_4 \ }\)になる。
このとき全事象の確率は\(\small{ \ P_0+P_1+P_2+P_3+P_4=1 \ }\)だから、\(\small{ \ 2 \ }\)個以上取り出す確率\(\small{ \ P_2+P_3+P_4 \ }\)を直接求めるより、\(\small{ \ 2 \ }\)個未満取り出す確率\(\small{ \ P_0+P_ 1 \ }\)を求めて、\(\small{ \ 1-P_0-P_1 \ }\)を計算した方が計算量が少ないのがわかるよね。
こんな風に求める事象の確率を\(\small{ \ P(\mathrm{A}) \ }\)とすると、\(\small{ \ P(\mathrm{A}) \ }\)を直接求めるよりも、\(\small{ \ P(\overline{\mathrm{A}}) \ }\)を求めて、\(\small{ \ P(A)+P(\overline{\mathrm{A}})=1 \ }\)から\(\small{ \ P(\mathrm{A}) \ }\)を求める方が簡単な場合って結構あるんだ。
もちろん直接\(\small{ \ P_2+P_3+P_4 \ }\)を求めても答えは出るんだけど、計算量が多くなるから、余事象の確率が使えるときは常に使うように心がけよう。
じゃあ、いつ余事象の確率が利用できるかというと、問題文に「少なくとも〜」って言葉が入っていたら余事象を考えよう。
それ以外にも使えるところはあるけど、まずは「少なくとも〜」って言葉を見たら余事象を考えるって覚えておこう。
上の問題も「\(\small{ \ 2 \ }\)個以上」って言い方は「少なくとも\(\small{ \ 2 \ }\)個」って言いかえられるよね。
\(\small{ \ 3 \ }\)個のさいころを同時に投げて出た目の積が次の数となる確率を求めよ。
(1)奇数
(2)\(\small{ \ 2 \ }\)の倍数
(3)\(\small{ \ 4 \ }\)の倍数
(1)積が奇数になるのは奇数だけ出るとき\(\small{ \ \left(\displaystyle\frac{1}{2}\right)^3=\displaystyle\frac{1}{8} \ }\)
(2)積が\(\small{ \ 2 \ }\)の倍数になるのは、少なくとも\(\small{ \ 1 \ }\)回は偶数の目が出るときよって余事象を考えて「偶数の目が出ない確率」を\(\small{ \ 1 \ }\)から引けばよい\(\small{ \ 1-\left(\displaystyle\frac{1}{2}\right)^3=\displaystyle\frac{7}{8} \ }\)
(3)余事象「\(\small{ \ 4 \ }\)で割り切れない確率」を考える\(\small{ \ 4 \ }\)で割り切れないのは
(i)奇数の目しか出ない
(ii)\(\small{ \ 2 \ }\)の目が\(\small{ \ 1 \ }\)回、奇数の目が\(\small{ \ 2 \ }\)回出る
(iii)\(\small{ \ 6 \ }\)の目が\(\small{ \ 1 \ }\)回、奇数の目が\(\small{ \ 2 \ }\)回出る
この(i)~(iii)\(\small{ \ 3 \ }\)通り
(i)の確率は\(\small{ \ \left(\displaystyle\frac{1}{2}\right)^3=\displaystyle\frac{1}{8} \ }\)
(ii)の確率は\(\small{ \ \displaystyle\frac{1}{6}\times\left(\displaystyle\frac{1}{2}\right)^2\times3=\displaystyle\frac{1}{8} \ }\)
(iii)の確率は\(\small{ \ \displaystyle\frac{1}{6}\times\left(\displaystyle\frac{1}{2}\right)^2\times3=\displaystyle\frac{1}{8} \ }\)
よって求める確率は
\(\small{ \ 1-\left(\displaystyle\frac{1}{8}+\displaystyle\frac{1}{8}+\displaystyle\frac{1}{8}\right)=\displaystyle\frac{5}{8} \ }\)
Point 確率の基本性質
①積事象・和事象の計算に注意する
②排反を利用したの計算は掛け算ではなく足し算
③「少なくとも」は余事象を利用する
サイコロをくり返し\(\small{ \ n \ }\)回振って、出た目の数を掛け合わせた積を\(\small{ \ X \ }\)とする。すなわち\(\small{ \ k \ }\)回目に出た目の数を\(\small{ \ Y_k \ }\)とすると、\(\small{ \ X=Y_1Y_2\cdots Y_n \ }\)である。
このとき次の問いに答えよ。
(1)\(\small{ \ X \ }\)が\(\small{ \ 3 \ }\)で割り切れる確率\(\small{ \ p_n \ }\)を求めよ。
(2)\(\small{ \ X \ }\)が\(\small{ \ 4 \ }\)で割り切れる確率\(\small{ \ q_n \ }\)を求めよ。
(3)\(\small{ \ X \ }\)が\(\small{ \ 6 \ }\)で割り切れる確率\(\small{ \ r_n \ }\)を求めよ。
(1)
\(\small{ \ X \ }\)が\(\small{ \ 3 \ }\)で割り切れるのは少なくとも\(\small{ \ 1 \ }\)回は\(\small{ \ 3 \ }\)か\(\small{ \ 6 \ }\)がでるとき
だから余事象の\(\small{ \ 1, \ 2, \ 4, \ 5 \ }\)しかでない確率を\(\small{ \ 1 \ }\)から引けばよい
よって求める確率は
\(\small{ \ p_n=1-\left(\displaystyle\frac{4}{6}\right)^n=1-\left(\displaystyle\frac{2}{3}\right)^n \ }\)
(2)
\(\small{ \ X \ }\)が\(\small{ \ 4 \ }\)で割り切れないのは
(i)\(\small{ \ n \ }\)回とも奇数がでる
(ii)\(\small{ \ 2 \ }\)または\(\small{ \ 6 \ }\)が\(\small{ \ 1 \ }\)回だけでて、残りは奇数がでる
(i)の確率は\(\small{ \ \left(\displaystyle\frac{3}{6}\right)^n=\left(\displaystyle\frac{1}{2}\right)^n \ }\)
(ii)の確率は\(\small{ \ {}_n\mathrm{C}_1\displaystyle\frac{2}{6}\cdot\left(\displaystyle\frac{3}{6}\right)^{n-1}=\displaystyle\frac{n}{3}\left(\displaystyle\frac{1}{2}\right)^{n-1} \ }\)
よって求める確率は
\(\small{ \ q_n=1-\left(\displaystyle\frac{1}{2}\right)^n-\displaystyle\frac{n}{3}\left(\displaystyle\frac{1}{2}\right)^{n-1} \ }\)
(3)
積が\(\small{ \ 2 \ }\)の倍数である確率を\(\small{ \ P(A) \ }\)
積が\(\small{ \ 3 \ }\)の倍数である確率を\(\small{ \ P(B) \ }\)とする
求める確率\(\small{ \ r_n=P(A\cap B) \ }\)

\(\small{ \ P(A) \ }\)は少なくとも偶数が\(\small{ \ 1 \ }\)回は出る確率だから
\(\small{ \ P(A)=1-\left(\displaystyle\frac{3}{6}\right)^n=1-\left(\displaystyle\frac{1}{2}\right)^n \ }\)
\(\small{ \ P(B) \ }\)は少なくとも\(\small{ \ 3 \ }\)の倍数が\(\small{ \ 1 \ }\)回は出る確率だから
\(\small{ \ P(B)=1-\left(\displaystyle\frac{4}{6}\right)^n=1-\left(\displaystyle\frac{2}{3}\right)^n \ }\)
\(\small{ \ P(\overline{A\cup B}) \ }\)は積が偶数でも\(\small{ \ 3 \ }\)の倍数でもない確率だから\(\small{ \ 1 \ }\)と\(\small{ \ 5 \ }\)だけ出る確率になる
\(\small{ \ P(\overline{A\cup B})=\left(\displaystyle\frac{2}{6}\right)^n=\left(\displaystyle\frac{1}{3}\right)^n \ }\)
よって求める確率は