組立除法の仕組みと使い方

こんにちは、リンス(@Lins016)です。
今回は組立除法の仕組みと使い方について学習していこう。

組立除法とは

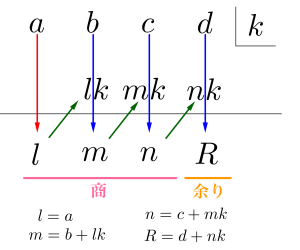
組立除法とは多項式$\small{ \ P(x) \ }$を一次式$\small{ \ x-k \ }$で割ったときの商$\small{ \ Q(x) \ }$と余り$\small{ \ R \ }$を簡単に求めることが出来る計算方法のこと。

整式の割り算でも代用することができるけど、組立除法の方が楽で早く計算できるから組立除法を使っていない人は使いこなせるように練習しよう。

組立除法

$\small{ \ ax^3+bx^2+cx+d=(x-k)(lx^2+mx+n)+R \ }$のとき

$$\begin{eqnarray} \left\{ \begin{array}{l} l=a\\ m=b+lk\\ n=c+mk\\ R=d+nk \end{array} \right. \end{eqnarray}$$

組立除法のやり方

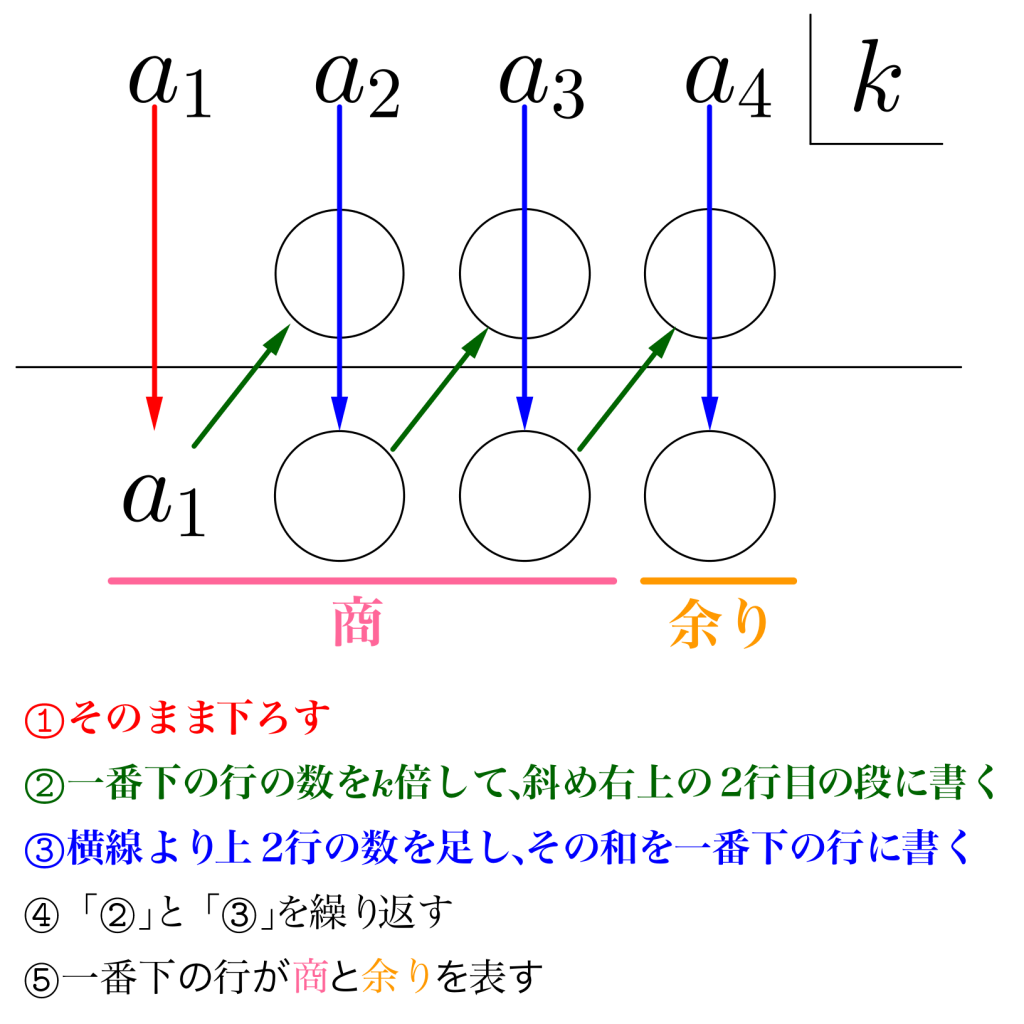
$\small{ \ a_1x^3+a_2x^2+a_3x+a_4 \ }$を$\small{ \ x-k \ }$で割った商と余りを組立除法で計算してみよう。
まずは一行目に割られる式の係数$\small{ \ a_1, \ a_2, \ a_3, \ a_4 \ }$を書き、その右に$\small{ \ k \ }$を書こう。

組立除法の利用（基本）

$\small{ \ (x^3-7x-6)\div (x+2) \ }$の商と余りを組立除法で求めてみよう。
一行目に割られる式を降べきの順に並べ、その係数$\small{ \ 1, \ 0, \ -7, \ -6 \ }$を左から順に書き、その右に割る式$\small{ \ x+2 \ }$を$\small{ \ 0 \ }$にするときの$\small{ \ x \ }$の値$\small{ \ -2 \ }$を書こう。

$\small{ \ x^2 \ }$の項は式にないけど、$\small{ \ 0x^2 \ }$のことだから、係数$\small{ \ 0 \ }$を書くのを忘れないようにしよう。

・計算のやり方
一番左の$\small{ \ 1 \ }$はそのまま下に下ろす。
この数$\small{ \ (1) \ }$と右上の数$\small{ \ (-2) \ }$を掛けた$\small{ \ 1\times(-2)=-2 \ }$を次の列の$\small{ \ 0 \ }$の下に書き、$\small{ \ 0 \ }$と$\small{ \ -2 \ }$の和をその下に書く。
更にその和$\small{ \ (-2) \ }$と右上の数$\small{ \ (-2) \ }$を掛けた$\small{ \ -2\times(-2)=4 \ }$を$\small{ \ -7 \ }$の下に書き、$\small{ \ -7 \ }$と$\small{ \ 4 \ }$の和をその下に書く。
更にその和$\small{ \ (-3) \ }$と右上の数$\small{ \ (-2) \ }$を掛けた$\small{ \ -3\times(-2)=6 \ }$を$\small{ \ -6 \ }$の下に書き、$\small{ \ -6 \ }$と$\small{ \ 6 \ }$の和をその下に書く。

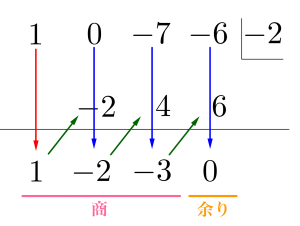
これで一番下の行にある数$\small{ \ 1, \ -2, \ -3, \ 0 \ }$から、$\small{ \ 1, \ -2, \ -3 \ }$が商の係数、つまり商が$\small{ \ x^2-2x-3 \ }$、一番右の数字$\small{ \ 0 \ }$が余りになるから、余り$\small{ \ 0 \ }$ってことが分かる。
つまり$\small{ \ (x^3-7x-6)=(x+2)(x^2-2x+3) \ }$が成り立つんだ。

組立除法の図の赤の矢印はそのまま下ろす、緑の矢印は右上の$\small{ \ -2 \ }$と掛ける、青い矢印は$\small{ \ 1 \ }$行目と$\small{ \ 2 \ }$行目を足すを表してるからね。

組立除法の仕組み

組立除法の計算がなぜ成り立つのか考えてみよう。

$\small{ \ ax^3+bx^2+cx+d \ }$を$\small{ \ x-k \ }$で割った商を$\small{ \ lx^2+mx+n \ }$、余りを$\small{ \ R \ }$とすると

右辺を展開して整理すると

係数を比較して
$\small{ \ \begin{eqnarray} \left\{ \begin{array}{l} a=l\\ b=m-lk\\ c=n-mk\\ d=R-nk \end{array} \right. \end{eqnarray} \ }$
よって
$\small{ \ \begin{eqnarray} \left\{ \begin{array}{l} l=a\\ m=b+lk\\ n=c+mk\\ R=d+nk \end{array} \right. \end{eqnarray} \ }$
が成り立つ。

この式が組立除法の計算を表してるんだ。

組立除法の利用（分数の場合）

$\small{ \ (8x^3-4x^2-10x-1)\div (2x+1) \ }$の商と余りを計算しよう。
この計算の場合、割る一次式の係数が$\small{ \ 1 \ }$でじゃないから分数を代入することになるよね。
この場合、最後に工夫が必要になるから注意しよう。

組立除法を使って計算すると

$\small{\begin{eqnarray} \ &&8x^3-4x^2-10x-1\\ &=&\left(x+\displaystyle\frac{1}{2}\right)(8x^2-8x-6)+2 \ \end{eqnarray}}$

ってことになるよね。
でも商の$\small{ \ 8x^2-8x-6 \ }$は$\small{ \ x+\displaystyle\frac{1}{2} \ }$で割った商を示してるんだ。

$\small{\begin{eqnarray} \ &&8x^3-4x^2-10x-1\\ &=&\left(x+\displaystyle\frac{1}{2}\right)(8x^2-8x-6)+2\\[8pt] &=&\left(2x+1\right)(4x^2-4x-3)+2 \ \end{eqnarray}}$
って変形する必要があるから注意しよう。

だから組立除法の計算では最後にこの商の部分を$\small{ \ 2 \ }$で割ることで$\small{ \ 2x+1 \ }$で割った商を求めることができるからね。

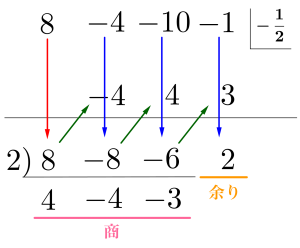
割る一次式の係数が$\small{ \ 1 \ }$じゃないときに組立除法を利用する場合は注意して答えを出そう。

組立除法と整式の割り算の違い

多項式$\small{ \ P(x) \ }$を一次式$\small{ \ x-k \ }$で割ったときの商$\small{ \ Q(x) \ }$と余り$\small{ \ R \ }$を求めるのは組立除法じゃなくて整式の割り算でもいいよね。

この組立除法と整式の割り算の違いを$\small{ \ x^3-7x-6 \ }$を$\small{ \ x+2 \ }$で割った商と余りを求める場合で考えてみよう。

組立除法は$\small{ \ x+2 \ }$の$\small{ \ +2 \ }$を$\small{ \ -2 \ }$にして、かけて足していくのに対して、整式の割り算は$\small{ \ x+2 \ }$のまま、かけて引いていくのが分かるよね。
やっていることは同じだけど、引き算するより足し算した方が簡単だよね。

数学はただ解けるだけじゃダメで、早くミスなく解く必要があるよね。整式の割り算でいつも計算している人は、組立除法を使えるように練習しておこう。
慣れたら絶対こっちのほうが早く計算できるようになるからね。

Point 組立除法の仕組みと使い方

①組立除法は必ずマスターする
②整式の割り算よりも組立除法を利用する