空間ベクトルの位置ベクトル応用

こんにちは、リンス(@Lins016)です。
今回は空間ベクトルの位置ベクトル応用について学習していこう。

空間ベクトルの位置ベクトル応用

今回は一つの問題を解きながら今まで学習した内容を確認していこう。

問題の確認

始点の変更

空間ベクトルに限らずベクトルの問題ではまずは始点を揃えることから始めよう。

四面体\(\small{ \ \mathrm{ABCD} \ }\)の場合、点\(\small{ \ \mathrm{O} \ }\)を始点にするんじゃなくて、点\(\small{ \ \mathrm{A} \ }\)を始点にする方が文字が少なくて済むから点\(\small{ \ \mathrm{A} \ }\)を始点にしよう。

\(\small{ \ \overrightarrow{\mathrm{AP}}+2 \overrightarrow{\mathrm{BP}}+3 \overrightarrow{\mathrm{CP}}+4 \overrightarrow{\mathrm{DP}}= \overrightarrow{\mathrm{0}} \ }\)

\(\small{\begin{eqnarray} \ 10\overrightarrow{\mathrm{AP}}&=&2 \overrightarrow{\mathrm{AB}}+3 \overrightarrow{\mathrm{AC}}+4 \overrightarrow{\mathrm{AD}}\\
&=&\displaystyle\frac{1}{5} \overrightarrow{\mathrm{AB}}+ \displaystyle\frac{3}{10} \overrightarrow{\mathrm{AC}}+ \displaystyle\frac{2}{5}\overrightarrow{\mathrm{AD}} \ \end{eqnarray}}\)

これはベクトルを表しただけで、まだ問題文の「位置について答えよ。」の答えにはなってないから注意してね。

存在範囲の利用

次に点\(\small{ \ \mathrm{P} \ }\)と平面\(\small{ \ \mathrm{BCD} \ }\)の位置関係について考えてみよう。
\(\small{ \ \overrightarrow{\mathrm{AP}}=\displaystyle\frac{1}{5} \overrightarrow{\mathrm{AB}}+ \displaystyle\frac{3}{10} \overrightarrow{\mathrm{AC}}+ \displaystyle\frac{2}{5}\overrightarrow{\mathrm{AD}} \ }\)

このとき各ベクトルの係数の和は
\(\small{ \ \displaystyle\frac{1}{5}+ \displaystyle\frac{3}{10}+ \displaystyle\frac{2}{5}= \displaystyle\frac{9}{10}\lt1 \ }\)だから平面\(\small{ \ \mathrm{BCD} \ }\)より点\(\small{ \ \mathrm{A} \ }\)側にあるっていえる。

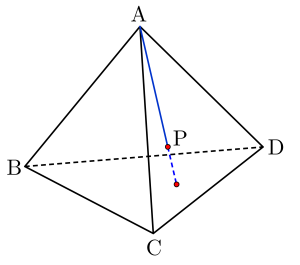
これは空間ベクトルの存在範囲で学習した点\(\small{ \ \mathrm{P} \ }\)が\(\small{ \ \overrightarrow{\mathrm{AP}}=s\overrightarrow{\mathrm{AB}}+t\overrightarrow{\mathrm{AC}}+u \overrightarrow{\mathrm{AD}} \ }\)のとき\(\small{ \ s+t+u=1 \ }\)なら点\(\small{ \ \mathrm{P} \ }\)は平面\(\small{ \ \mathrm{BCD} \ }\)上にあるってことの応用になるからね。

これを利用して平面\(\small{ \ \mathrm{BCD} \ }\)と点\(\small{ \ \mathrm{P} \ }\)の位置関係を考えてみよう。
まずは係数を通分しよう。
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AP}}&=&\displaystyle\frac{1}{5} \overrightarrow{\mathrm{AB}}+ \displaystyle\frac{3}{10} \overrightarrow{\mathrm{AC}}+ \displaystyle\frac{2}{5}\overrightarrow{\mathrm{AD}}\\[10pt] &=&\displaystyle\frac{2 \overrightarrow{\mathrm{AB}}+3 \overrightarrow{\mathrm{AC}}+4\overrightarrow{\mathrm{AD}}}{10} \ \end{eqnarray}}\)

次に分母を前にだして、分子の係数の和を前の分子と後ろの分母につける。
\(\small{ \ \overrightarrow{\mathrm{AP}}=\displaystyle\frac{9}{10 }\cdot\displaystyle\frac{2 \overrightarrow{\mathrm{AB}}+3 \overrightarrow{\mathrm{AC}}+4\overrightarrow{\mathrm{AD}}}{9} \ }\)

これで\(\small{ \ \displaystyle\frac{2 \overrightarrow{\mathrm{AB}}+3 \overrightarrow{\mathrm{AC}}+4\overrightarrow{\mathrm{AD}}}{9} \ }\)の各ベクトルの係数の和は\(\small{ \ 1 \ }\)になるから\(\small{ \ \overrightarrow{\mathrm{AQ}}=\displaystyle\frac{2 \overrightarrow{\mathrm{AB}}+3 \overrightarrow{\mathrm{AC}}+4\overrightarrow{\mathrm{AD}}}{9} \ }\)とすると点\(\small{ \ \mathrm{Q} \ }\)は平面\(\small{ \ \mathrm{BCD} \ }\)上にあるって言えるよね。

\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AP}}&=&\displaystyle\frac{9}{10 }\cdot\displaystyle\frac{2 \overrightarrow{\mathrm{AB}}+3 \overrightarrow{\mathrm{AC}}+4\overrightarrow{\mathrm{AD}}}{9}\\[10pt] &=&\displaystyle\frac{9}{10 }\overrightarrow{\mathrm{AQ}} \ \end{eqnarray}}\)
ってなるから
点\(\small{ \ \mathrm{P} \ }\)は点\(\small{ \ \mathrm{A} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)を\(\small{ \ 9:1 \ }\)に内分する点ってことがわかったよね。

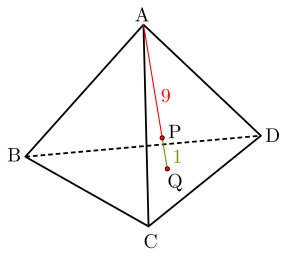
内分の公式を利用

次に内分の公式を利用して、点\(\small{ \ \mathrm{Q} \ }\)の位置を考えていこう。
\(\small{ \ \overrightarrow{\mathrm{AQ}}=\displaystyle\frac{2 \overrightarrow{\mathrm{AB}}+3 \overrightarrow{\mathrm{AC}}+4\overrightarrow{\mathrm{AD}}}{9} \ }\)

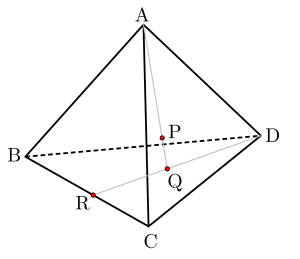
点\(\small{ \ \mathrm{Q} \ }\)は平面\(\small{ \ \mathrm{BCD} \ }\)上の点で、直線\(\small{ \ \mathrm{QD} \ }\)と線分\(\small{ \ \mathrm{BC} \ }\)の交点を\(\small{ \ \mathrm{R} \ }\)として
\(\small{ \ \mathrm{BR:RC} \ }\)と\(\small{ \ \mathrm{RQ:QD} \ }\)を考えてみよう。

\(\small{ \ \overrightarrow{\mathrm{AQ}}=\displaystyle\frac{2 \overrightarrow{\mathrm{AB}}+3 \overrightarrow{\mathrm{AC}}+4\overrightarrow{\mathrm{AD}}}{9} \ }\)
を式変形すると
\(\small{ \ \overrightarrow{\mathrm{AQ}}=\displaystyle\frac{5}{9}\cdot \displaystyle\frac{2\overrightarrow{\mathrm{AB}}+3 \overrightarrow{\mathrm{AC}}}{5}+ \displaystyle\frac{4}{9}\overrightarrow{\mathrm{AD}} \ }\)
ってなるよね。

このとき\(\small{ \ \displaystyle\frac{2\overrightarrow{\mathrm{AB}}+3 \overrightarrow{\mathrm{AC}}}{5} \ }\)は係数の和が \(\small{ \ 1 \ }\)だから\(\small{ \ \mathrm{BC} \ }\)上にあって、内分の式から\(\small{ \ \mathrm{BC} \ }\)を\(\small{ \ 3:2 \ }\)に内分するって言えるよね。

内分や外分はベクトルで最頻出な範囲だから、きちんと理解しておこう。

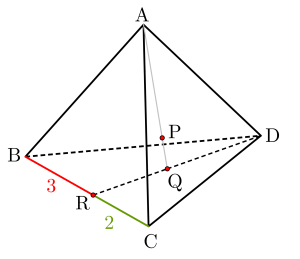
この\(\small{ \ \mathrm{BC} \ }\)を\(\small{ \ 3:2 \ }\)に内分する点を\(\small{ \ \mathrm{R} \ }\)とすると\(\small{ \ \overrightarrow{\mathrm{AR}}=\displaystyle\frac{2\overrightarrow{\mathrm{AB}}+3 \overrightarrow{\mathrm{AC}}}{5} \ }\)になるから
\(\small{ \ \overrightarrow{\mathrm{AQ}}=\displaystyle\frac{5}{9}\overrightarrow{\mathrm{AR}}+\displaystyle\frac{4}{9}\overrightarrow{\mathrm{AD}} \ }\)になるよね。
この式も係数の和が\(\small{ \ 1 \ }\)になるから点\(\small{ \ \mathrm{Q} \ }\)は\(\small{ \ \mathrm{RD} \ }\)上にあって、内分の式から\(\small{ \ \mathrm{RD} \ }\)を\(\small{ \ 4:5 \ }\)に内分する点って言えるよね。

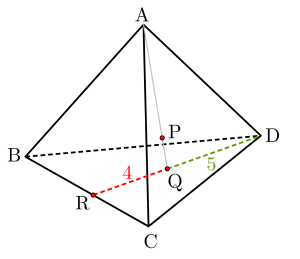
だから答えは「求める点\(\small{ \ \mathrm{P} \ }\)の位置は、線分\(\small{ \ \mathrm{BC} \ }\)を\(\small{ \ 3:2 \ }\)に内分する点を\(\small{ \ \mathrm{R} \ }\)、線分\(\small{ \ \mathrm{RD} \ }\)を\(\small{ \ 4:5 \ }\)に内分する点を\(\small{ \ \mathrm{Q} \ }\)とすると、線分\(\small{ \ \mathrm{AQ} \ }\)を\(\small{ \ 9:1 \ }\)に内分する点」になるんだ。

この問題はどの問題集にも取り上げられている問題で、簡単に係数を変形して答えてる問題だけど、空間ベクトルの位置ベクトルの大切な考え方を理解するのにいい問題だから、今まで学習した範囲のリンク先もチェックしておこう。

補足

\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AQ}}&=&\displaystyle\frac{2 \overrightarrow{\mathrm{AB}}+3 \overrightarrow{\mathrm{AC}}+4\overrightarrow{\mathrm{AD}}}{9}\\[8pt] &=&\displaystyle\frac{5}{9}\cdot \displaystyle\frac{2\overrightarrow{\mathrm{AB}}+3\overrightarrow{\mathrm{AC}}}{5}+ \displaystyle\frac{4}{9}\overrightarrow{\mathrm{AD}}\\[8pt] &=&\displaystyle\frac{5}{9}\overrightarrow{\mathrm{AR}}+\displaystyle\frac{4}{9}\overrightarrow{\mathrm{AD}} \ \end{eqnarray}}\)
この式変形の部分だけど、一行目の\(\small{ \ \displaystyle\frac{2\overrightarrow{\mathrm{AB}}+3 \overrightarrow{\mathrm{AC}}}{9} \ }\)の部分は\(\small{ \ \overrightarrow{\mathrm{AR}} \ }\)の実数倍になることは内分点のベクトルの式からわかっているからね。

だって\(\small{ \ \mathrm{RD} \ }\)を内分する\(\small{ \ \overrightarrow{\mathrm{AQ}} \ }\)は\(\small{ \ \overrightarrow{\mathrm{AR}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{AD}} \ }\)からできていて、\(\small{ \ \overrightarrow{\mathrm{AB}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{AC}} \ }\)は\(\small{ \ \overrightarrow{\mathrm{AD}} \ }\)には含まれないから、一行目の\(\small{ \ \displaystyle\frac{2\overrightarrow{\mathrm{AB}}+3 \overrightarrow{\mathrm{AC}}}{9} \ }\)の部分は\(\small{ \ \overrightarrow{\mathrm{AR}} \ }\)の実数倍になるってことだよね。

つまり\(\small{ \ \overrightarrow{\mathrm{AB}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{AC}} \ }\)の係数の比が\(\small{ \ \mathrm{BC} \ }\)の内分の比になるってことなんだ。

Point　空間ベクトル位置ベクトル応用

①係数の和を\(\small{ \ 1 \ }\)にして平面上や直線上の点を表すベクトルを求める