こんにちは、リンス(@Lins016)です。
今回は三角形の成立条件と鋭角・直角・鈍角三角形について学習していこう。
三角形の成立条件や角の大きさは辺の長さを利用
今回は三角形の成立条件や角の大きさについて考えていこう。
角の大きさ
鋭角\(\small{ \ 0^{\circ} \lt \theta \lt 90^{\circ} \ }\)
直角\(\small{ \ \theta =90^{\circ} \ }\)
鈍角\(\small{ \ 90^{\circ} \lt \theta \lt 180^{\circ} \ }\)
三角形の成立条件
\(\small{ \ |b-c| \lt a \lt b+c \ }\)
辺と対角の関係
\(\small{ \ a \gt b \ \ \Longleftrightarrow \ \angle \mathrm{A} \gt \angle \mathrm{B} \ }\)
\(\small{ \ a =b \ \ \Longleftrightarrow \ \angle \mathrm{A} = \angle \mathrm{B} \ }\)
\(\small{ \ a \lt b \ \ \Longleftrightarrow \ \angle \mathrm{A} \lt \angle \mathrm{B} \ }\)
三角形の成立条件
三角形ができるためには1辺の長さがその他の2辺の長さの和より短くないといけない。1辺の長さがその他の2辺の和より長くなると2辺を結ぶことが出来ないよね。
だから次の式が成り立つんだ。
\(\small{ \ a\lt b+c \ }\)
\(\small{ \ b\lt a+c \ }\)
\(\small{ \ c\lt a+b \ }\)
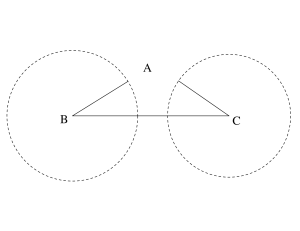
これを一つの文字に注目すると\(\small{ \ |b-c| \lt a \lt b+c \ }\)になる。この式が三角形の成立条件になるからね。
ただ、一番長い辺が分かっている場合は、一番長い辺がその他の2辺の和より短いっていう右側の\(\small{ \ a\lt b+c \ }\)の不等式だけでいいよ。だって一番長いって分かっているから\(\small{ \ |b-c| \lt a \ }\)は成り立つに決まってるからね。
三角形の辺の長さを\(\small{ \ x \ }\)として求めるときは成立条件にも気をつけるようにしよう。
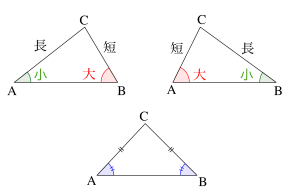
辺の長さと対角の関係
辺の長さと対角の大きさには次の関係式が成り立つ。
\(\small{ \ a \gt b \ \ \Longleftrightarrow \ \angle \mathrm{A} \gt \angle \mathrm{B} \ }\)
\(\small{ \ a =b \ \ \Longleftrightarrow \ \angle \mathrm{A} = \angle \mathrm{B} \ }\)
\(\small{ \ a \lt b \ \ \Longleftrightarrow \ \angle \mathrm{A} \lt \angle \mathrm{B} \ }\)
つまり辺の長さが長い方が対角が大きいってことが言えるからね。
正弦定理や余弦定理で辺の長さや角度を求める場合、このことを頭に入れて答えを導こう。
鋭角三角形・直角三角形・鈍角三角形
三角形には鋭角三角形・直角三角形・鈍角三角形がある。ここで注意しないといけないのが、どの三角形も2つの角は鋭角ってこと。だから一番長い辺の対角が鋭角か直角か鈍角かってことを判断しないといけないからね。
ちなみに何で判断するかということ余弦定理を利用しよう。
\(\small{ \ \cos \theta \ }\)(余弦)が正だと鋭角、\(\small{ \ 0 \ }\)だと直角、負だと鈍角になるからね。正弦だとどの角も正になるから判断できないよね。
\(\small{ \ \cos \mathrm{C}= \displaystyle \frac{a^2+b^2-c^2}{2ab} \ }\)より右辺の分母は常に正だから、分子が正か0か負になることを考えればいいから\(\small{ \ a^2+b^2-c^2 \ }\)の符号を考えればいい。ってことはここから直角三角形の三平方の定理も言えることがわかるね。
\(\small{ \ \triangle \mathrm{ABC} \ }\)の\(\small{ \ 3 \ }\)辺が\(\small{ \ 2a+3b-3c=0\cdots① \ }\)、\(\small{ \ 3a+b-2c=0\cdots② \ }\)を満たすとき、\(\small{ \ \triangle \mathrm{ABC} \ }\)は鋭角三角形、直角三角形、鈍角三角形のうちどれか答えよ。
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
2a+3b-3c=0\cdots①\\
3a+b-2c=0\cdots②
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて\(\small{ \ c=\displaystyle \frac{7}{3}a, \ b=\displaystyle \frac{5}{3}a \ }\)
よって\(\small{ \ a \lt b \lt c \ }\)より
一番大きい\(\small{ \ \angle \mathrm{C} \ }\)の余弦を調べると
\(\small{\begin{eqnarray} \ \cos \mathrm{C}&=&\displaystyle \frac{a^2-\left(\displaystyle \frac{5}{3}a\right)^2-\left(\displaystyle \frac{7}{3}a\right)^2}{2\cdot a \cdot\displaystyle \frac{5}{3}a}\\
&=&\displaystyle \frac{-\displaystyle \frac{5}{3}a^2}{\displaystyle \frac{10}{3}a^2}=-\displaystyle \frac{1}{2} \ \end{eqnarray}}\)
つまり\(\small{ \ \angle\mathrm{C}=120^{\circ} \ }\)より\(\small{ \ \triangle \mathrm{ABC} \ }\)は鈍角三角形である

Point
①辺や角の大きさを求めるときは三角形の成立条件や対角(辺)との大小関係に注意しよう
②鋭角・直角・鈍角の見極めは余弦定理を利用しよう
長さ\(\small{ \ a , \ b \ }\)の二つの線分と大きさ\(\small{ \ \theta \ (0^{\circ}\lt \theta \lt 180^{\circ}) \ }\)の角が与えられている。
\(\small{ \ \mathrm{BC}=a \ }\)、\(\small{ \ \mathrm{AC}=b \ }\)、\(\small{ \ \angle\mathrm{A}=\theta \ }\)となる\(\small{ \ \triangle \mathrm{ABC} \ }\)が作れるための\(\small{ \ a , \ b, \ \theta \ }\)の条件を求めよ。
\(\small{ \ a\gt0, \ b\gt0, \ 0^{\circ}\lt \theta \lt 180^{\circ} \ }\)
\(\small{ \ \mathrm{AB}=x\gt0 \ }\)とする。
余弦定理より
\(\small{ \ a^2=x^2+b^2-2bx\cos\theta \ }\)
\(\small{ \ \therefore x^2-2(b\cos\theta)x+b^2-a^2=0\ }\)
よってこの二次方程式が正の解を持てば三角形が作れる。
\(\small{ \ f(x)= x^2-2(b\cos\theta)x+b^2-a^2 \ }\)とすると
\(\small{ \begin{eqnarray}\ f(x)&=&(x-b\cos\theta)^2-b^2\cos^2\theta+b^2-a^2\\
&=&(x-b\cos\theta)^2+b^2\sin^2\theta-a^2 \ \end{eqnarray}}\)
(i)\(\small{ \ b\cos \theta \gt 0 \ }\)\(\small{ \ \therefore 0^{\circ}\lt \theta \lt 90^{\circ} \ }\)のとき
\(\small{ \ b^2\sin^2\theta-a^2 \leqq0 \ }\)であればよい
\(\small{ \ (b\sin\theta-a)(b\sin\theta+a)\leqq 0 \ }\)
\(\small{ \ -a \leqq b\sin \theta \leqq a \ }\)
\(\small{ \ b\sin \theta \gt 0) \ }\)より
\(\small{ \ \therefore 0 \lt b\sin\theta \leqq a \ }\)
(ii)\(\small{ \ b\cos \theta \leqq 0 \ }\)\(\small{ \ \therefore 90^{\circ}\leqq \theta \lt 180^{\circ} \ }\)のとき
\(\small{ \ f(0)=b^2-a^2 \lt 0 \ }\)であればよいので
\(\small{ \ \therefore 0 \lt b \lt a \ }\)

