こんにちは、リンス(@Lins016)です。
今回は三角方程式と単位円とグラフについて学習していこう。
グラフと単位円
前回学習した三角方程式の解き方では、三角関数の値を覚えて、置き換えや一般解を利用した解き方を学習したけど、今回は三角方程式を単位円とグラフを利用して考えてみよう。
三角方程式と単位円
単位円を利用した基本的な考え方は数学Ⅰの図形と計量で学習したところを利用するから、まずは次の記事を確認してから進めていこう。
-

三角比の方程式と不等式(基本)
単位円を利用した方程式・不等式の解き方について詳しく解説しています。
続きを見る
それじゃ次の三角方程式を単位円で考えていこう。
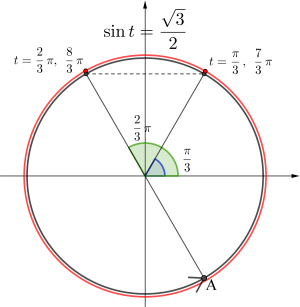
\(\small{ \ 0 \leqq \theta \lt 2\pi \ }\)のとき、\(\small{ \ \sin\left(2\theta-\displaystyle\frac{\pi}{3}\right)=\displaystyle\frac{\sqrt{3}}{2} \ }\)を解け。
\(\small{ \ 2\theta-\displaystyle\frac{\pi}{3}=t \ }\)とおくと、\(\small{ \ 0 \leqq \theta \lt 2\pi \ }\)より、
\(\small{ \ -\displaystyle\frac{\pi}{3} \leqq t \lt \displaystyle\frac{11}{3}\pi \ }\)になる。
つまり動径は図の点\(\small{ \ \mathrm{A} \ }\)から\(\small{ \ 2 \ }\)周回ることになるからね。
\(\small{ \ \theta \ }\)が\(\small{ \ 0 \leqq \theta \lt 2\pi \ }\)のとき、\(\small{ \ \theta \ }\)の係数が\(\small{ \ 2 \ }\)なら\(\small{ \ 2 \ }\)周回って、\(\small{ \ \theta \ }\)の係数が\(\small{ \ 3 \ }\)だったら\(\small{ \ 3 \ }\)周回ることになるんだ。
動径が\(\small{ \ y=\displaystyle\frac{\sqrt{3}}{2} \ }\)と交わる点が\(\small{ \ t \ }\)の解になる。

\(\small{ \ \sin t=\displaystyle\frac{\sqrt{3}}{2} \ }\)より\(\small{ \ t=\displaystyle\frac{\pi}{3}、\displaystyle\frac{2}{3}\pi、\displaystyle\frac{7}{3}\pi、\displaystyle\frac{8}{3}\pi \ }\)
この\(\small{ \ t \ }\)の解は動径が同じ位置の解なら\(\small{ \ 2\pi \ }\)ずつ離れているのが分かるよね。
あとはこれを\(\small{ \ \theta \ }\)の式に戻して解けばいいから、
\(\small{ \ 2\theta-\displaystyle\frac{\pi}{3}=\displaystyle\frac{\pi}{3}、\displaystyle\frac{2}{3}\pi、\displaystyle\frac{7}{3}\pi、\displaystyle\frac{8}{3}\pi \ }\)
\(\small{ \ \therefore \theta=\displaystyle\frac{\pi}{3}、\displaystyle\frac{\pi}{2}、\displaystyle\frac{4}{3}\pi、\displaystyle\frac{3}{2}\pi \ }\)
三角方程式とグラフ
さっきと同じ問題を今度はグラフのことを考えながら解いてみよう。
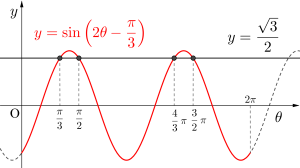
\(\small{ \ 0 \leqq \theta \lt 2\pi \ }\)のとき、\(\small{ \ \sin\left(2\theta-\displaystyle\frac{\pi}{3}\right)=\displaystyle\frac{\sqrt{3}}{2} \ }\)を解け。
\(\small{\begin{eqnarray} \ y&=&\sin\left(2\theta-\displaystyle\frac{\pi}{3}\right)\\[3pt]
&=&\sin2\left(\theta-\displaystyle\frac{\pi}{6}\right) \ \end{eqnarray}}\)
つまり\(\small{ \ y=\sin\left(2\theta-\displaystyle\frac{\pi}{3}\right) \ }\)のグラフは、\(\small{ \ y=\sin 2\theta \ }\)のグラフを\(\small{ \ x \ }\)軸方向に\(\small{ \ \displaystyle\frac{\pi}{6} \ }\)平行移動したグラフになる。
\(\small{ \ y=\sin 2\theta \ }\)の周期は\(\small{ \ \pi \ }\)だから、\(\small{ \ 0 \leqq \theta \lt 2\pi \ }\)では\(\small{ \ 2 \ }\)周期分になる。
だから\(\small{ \ \sin\left(2\theta-\displaystyle\frac{\pi}{3}\right) \ }\)と\(\small{ \ y=\displaystyle\frac{\sqrt{3}}{2} \ }\)との共有点は\(\small{ \ 4 \ }\)つある。
周期が\(\small{ \ \pi \ }\)だから一つ先の共有点との間隔は\(\small{ \ \pi \ }\)なのがわかるよね。

ただこのグラフの場合、\(\small{ \ \theta \ }\)の値を求めるためには、置き換えて単位円を利用するか、一般解を利用した\(\small{ \ 2\theta-\displaystyle\frac{\pi}{3}=\displaystyle\frac{\pi}{3}+2n\pi, \ \displaystyle\frac{2}{3}\pi+2n\pi \ }\)を解いて値を求める必要があるんだ。
だから、単に三角方程式を解くだけならグラフはあまり役立たないかもしれないけど、解の個数を求めたりする問題にはグラフを利用したりするから、きちんとグラフの形を頭に入れておこう。
グラフがきちんと書けない人はもう一度グラフの書き方を復習しておこう。
-

三角関数のグラフ(1)
sinとcosのグラフの注意する点について詳しく解説しています。
続きを見る
三角方程式と単位円とグラフ
三角方程式と単位円とグラフの関係が確認できたと思うけど、どの方法で三角方程式を解いても構わないからね。
ただ漠然と解き方だけ覚えるよりも、単位円を一緒に考えてみたり、グラフを考えてみたりすることで、より三角方程式を理解できるようになると思うからこの記事を書いたんだ。
だってより柔軟な考え方ができるようになれば、いろいろな対応できるかもしれないからね。
\(\small{ \ 0\leqq \theta \lt2\pi \ }\)のとき、\(\small{ \ 2\sin\left(2\theta+\displaystyle\frac{\pi}{4}\right)=1 \ }\)を解け。
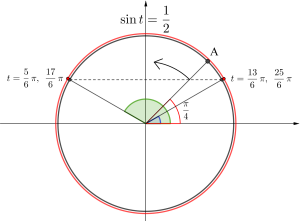
\(\small{ \ 2\sin\left(2\theta+\displaystyle\frac{\pi}{4}\right)=1 \ }\)
\(\small{ \ \sin\left(2\theta+\displaystyle\frac{\pi}{4}\right)=\displaystyle\frac{1}{2} \ }\)
\(\small{ \ t=2\theta+\displaystyle\frac{\pi}{4} \ }\)とする。
\(\small{ \ 0\leqq \theta \lt2\pi \ }\)より
\(\small{ \ \displaystyle\frac{\pi}{4}\leqq t \lt \displaystyle\frac{17}{4}\pi \ }\)
\(\small{ \ \sin t=\displaystyle\frac{1}{2} \ }\)より
\(\small{ \ t=\displaystyle\frac{5}{6}\pi, \ \displaystyle\frac{13}{6}\pi, \ \displaystyle\frac{17}{6}\pi, \ \displaystyle\frac{25}{6}\pi \ }\)
\(\small{ \ \theta=\displaystyle\frac{t-\displaystyle\frac{\pi}{4}}{2} \ }\)より
\(\small{ \ \theta=\displaystyle\frac{7}{24}\pi, \ \displaystyle\frac{23}{24}\pi, \ \displaystyle\frac{31}{24}\pi, \ \displaystyle\frac{47}{24}\pi \ }\)

Point 三角方程式と単位円とグラフ
①単位円を利用して三角方程式を解けるようになる
②三角方程式とグラフの関係を考える