点と直線の距離

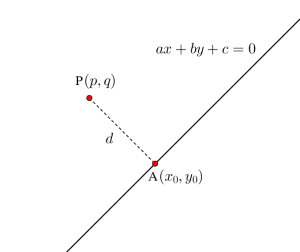
\(\small{ \ \mathrm{P}(p,q) \ }\)から直線に下ろした垂線の足の座標を\(\small{ \ \mathrm{A}(x_0,y_0) \ }\)とすると、求める長さ\(\small{ \ d \ }\)は
\(\small{ \ d=\sqrt{(p-x_0)^2+(q-y_0)^2} \cdots①\ }\)となる。
直線\(\small{ \ \mathrm{AP} \ }\)と\(\small{ \ ax+by+c=0 \ }\)は垂直だから、\(\small{ \ \mathrm{AP} \ }\)の傾きと直線の傾きの積は\(\small{ \ -1 \ }\)になる。
\(\small{ \ \displaystyle \frac{q-y_0}{p-x_0} \cdot \left(-\displaystyle \frac{a}{b}\right) =-1\ }\)
これを変形して
\(\small{ \ \displaystyle \frac{p-x_0}{a}=\displaystyle \frac{q-y_0}{b}=k \ }\)とおくと
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
x_0=p-ka\\
y_0=q-kb\\
\end{array}
\right.　\cdots②
\end{eqnarray} \ }\)
となる。
ここで点\(\small{ \ \mathrm{A}(x_0,y_0) \ }\)は直線上にあるから、\(\small{ \ ax_0+by_0+c=0 \ }\)を満たす。
これに②を代入すると、
\(\small{ \ a(p-ka)+b(q-kb)+c=0 \ }\)
\(\small{ \ k(a^2+b^2)=ap+bq+c \ }\)
\(\small{ \ \therefore k=\displaystyle \frac{ap+bq+c}{a^2+b^2}\cdots③ \ }\)
また\(\small{ \ ② \ }\)を\(\small{ \ ① \ }\)に代入すると
\(\small{\begin{eqnarray}
d&=&\sqrt{(p-x_0)^2+(q-y_0)^2} \\
&=&\sqrt{(ka)^2+(kb)^2}\\
&=&\vert k \vert \sqrt{a^2+b^2}
\end{eqnarray}　}\)
これに\(\small{ \ ③ \ }\)を代入して
\(\small{ \ d=\displaystyle \frac{\vert ap+bq+c \vert}{\sqrt{a^2+b^2}} \ }\)