こんにちは、リンス(@Lins016)です。
今回は二つの等差数列の共通項について学習していこう。
二つの等差数列の共通項も等差数列
二つの等差数列の共通項の数列も等差数列になってるから共通項の初項と公差を求めれば、一般項を求めることができるよね。
共通項の公差は、二つの数列の公差の最小公倍数になっていることに気付けば、あとは最初の共通項を見つければいいからね。
\(\small{ \ a_n=a_1+(n-1)d_1 \ }\)
\(\small{ \ b_n=b_1+(n-1)d_2 \ }\)
二つの等差数列の共通項の公差は\(\small{ \ d_1 \ }\)と\(\small{ \ d_2 \ }\)の最小公倍数
等差数列の一般項は\(\small{ \ pn+q \ }\)のような\(\small{ \ n \ }\)の一次式になっていて、\(\small{ \ n \ }\)の係数が公差になるから、二つの数列の一般項が与えられているときは\(\small{ \ n \ }\)の係数の最小公倍数を求めよう。
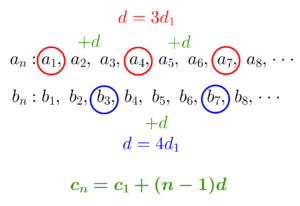
共通項の初項を見つけよう
共通項の公差は簡単に求めることができるけど、初項は公差のように簡単に求めることができない。
等差数列は初項が違うと全く異なる数列になるから、正確に初項を求めないといけないからね。
初項の求め方は書き出して求めてもいいし、計算式で求めても良い。
とにかく最初の共通項を間違いなく求めることが大切だ。
求めた共通項が元の二つの数列の項なのか必ず確認しよう。
初項\(\small{ \ 2 \ }\)公差\(\small{ \ 3 \ }\)の等差数列\(\small{ \ \{a_n\} \ }\)と初項\(\small{ \ 4 \ }\)公差\(\small{ \ 5 \ }\)の等差数列\(\small{ \ \{b_n\} \ }\)について、これらの数列に共通に含まれる項を順に並べてできた数列\(\small{ \ \{c_n\} \ }\)の一般項を求めよ。
共通項の公差は\(\small{ \ 3 \ }\)と\(\small{ \ 5 \ }\)の最小公倍数の\(\small{ \ 15 \ }\)である。
数列\(\small{ \ \{a_n\} \ }\)と\(\small{ \ \{b_n\} \ }\)を書き出すと
\(\small{ \ \{a_n\}:2、5、8、11、14、17、20、23\cdots \ }\)
\(\small{ \ \{b_n\}:4、9、14、19、24、29、34、39\cdots \ }\)
より共通項の初項は\(\small{ \ 14 \ }\)であることがわかる。
よって求める共通項\(\small{ \ \{c_n\} \ }\)の一般項は
\(\small{\begin{eqnarray} \ c_n&=&14+(n-1)\cdot15\\
&=&15n-1 \ \end{eqnarray}}\)
計算式での共通項の求め方
上の例題の共通項を計算で求めてみよう。数列\(\small{ \ \{a_n\} \ }\)の\(\small{ \ l \ }\)番目の項と\(\small{ \ \{b_n\} \ }\)の\(\small{ \ m \ }\)番目の項が共通だとすると\(\small{ \ a_l=b_m \ }\)より\(\small{ \ 3l-1=5m-1 \therefore 3l=5m \ }\)になる。
\(\small{ \ l, \ m \ }\)ともに整数で\(\small{ \ 3 \ }\)と\(\small{ \ 5 \ }\)は互いに素だから、\(\small{ \ l \ }\)は\(\small{ \ 5 \ }\)の倍数、\(\small{ \ m \ }\)は\(\small{ \ 3 \ }\)の倍数だよね。だから求める数列は\(\small{ \ \{a_n\} \ }\)の第\(\small{ \ 5n \ }\)項になるから\(\small{ \ c_n=3(5n)-1=15n-1 \ }\)になるんだ。
同様に\(\small{ \ \{b_n\} \ }\)で求めると\(\small{ \ \{b_n\} \ }\)の第\(\small{ \ 3n \ }\)項になるから\(\small{ \ c_n=5(3n)-1=15n-1 \ }\)になって同じになることがわかるよね。
ただ、与えられた数列によってはこの式のように簡単に処理しづらい問題もある。
例えば、\(\small{ \ a_n=3m-1 \ }\)、\(\small{ \ b_n=4n \ }\)のような数列の場合は、\(\small{ \ 3l-1=4m \ }\)にして、\(\small{ \ 3(l+1)=4(m+1) \ }\)という変形に気づけばいいけど、気付けなかったら\(\small{ \ 3l=4m+1 \ }\)に変形してもどうしようもないからね。
うまい変形に気付けなかったら一次不定方程式を解かないといけないから、それだったら書き出して初項を求めよう。

必ずもとの数列で成り立つか確認しよう。
Point 二つの等差数列の共通項
①二つの数列の公差の最小公倍数を共通項の数列の公差にしよう。
②共通項の初項を正確に求めよう。
自然数全体の集合を\(\small{ \ U \ }\)の部分集合の\(\small{ \ P=\{5n-3|n \ }\)は自然数\(\small{ \ \} \ }\)、\(\small{ Q=\{7n-3|n \ }\)は自然数\(\small{ \ \} \ }\)について次の問いに答えよ。
(1)\(\small{ \ P \cap Q \ }\)の要素を小さい順に\(\small{ \ a_1、a_2、a_3、\cdots、a_n、\cdots \ }\)とするとき\(\small{ \ \{a_n\} \ }\)の一般項を求めよ。
(2)\(\small{ \ U \ }\)に関する\(\small{ \ Q \ }\)の補集合を\(\small{ \ \overline{ Q } \ }\)とする。\(\small{ \ P\cap\overline{ Q } \ }\)の要素を小さい順に\(\small{ \ b_1、b_2、b_3、\cdots、b_n、\cdots \ }\)とするとき\(\small{ \ \{b_n\} \ }\)の値が\(\small{ \ 100 \ }\)を初めて超える\(\small{ \ n \ }\)を求めよ。
(1)\(\small{ \ P \ }\)の要素を小さい順に並べた数列を\(\small{ \ \{p_n\} \ }\)、\(\small{ \ Q \ }\)の要素を小さい順に並べた数列を\(\small{ \ \{q_n\} \ }\)とすると、共通項は\(\small{ \ p_l=q_m \ }\)を満たすから
\(\small{ \ 5l-3=7m-3 \quad \therefore 5l=7m\ }\)
\(\small{ \ 5 \ }\)と\(\small{ \ 7 \ }\)は互いに素だから\(\small{ \ l \ }\)は\(\small{ \ 7 \ }\)の倍数である。
よって求める共通項は\(\small{ \ \{p_n\} \ }\)の第\(\small{ \ 7n \ }\)項になるので
\(\small{\begin{eqnarray} \ a_n&=&5(7n)-3\\
&=&35n-3 \ \end{eqnarray}}\)
(2)\(\small{ \ P \ }\)の要素で\(\small{ \ 100 \ }\)以下の要素は\(\small{ \ 5n-3\lt 100 \ }\)より\(\small{ \ 20 \ }\)個あり、\(\small{ \ p_{20}=97 \ }\)である。
この\(\small{ \ 20 \ }\)個のうち\(\small{ \ P \cap Q \ }\)の要素は(1)より\(\small{ \ 32 \ }\)と\(\small{ \ 67 \ }\)の\(\small{ \ 2 \ }\)個だけであるから\(\small{ \ p_{20}=b_{18} \ }\)となる。
\(\small{ \ p_{21}=102 \ }\)でこれは\(\small{ \ P \cap Q \ }\)の要素だから\(\small{ \ p_{22}=107=b_{19} \ }\)となる。
よって初めて\(\small{ \ 100 \ }\)を超える\(\small{ \ n \ }\)は\(\small{ \ 19 \ }\)である。

