こんにちは、リンス(@Lins016)です。
今回は加法定理と二直線のなす角について学習していこう。
二直線のなす角と三角関数
二直線のなす角の問題は三角関数の加法定理を利用する解き方以外にもベクトルを利用したりとか色々あるけど、今回は加法定理の\(\small{ \ \tan\left(\alpha-\beta\right) \ }\)を利用した方法を学習していくからきちんと理解しておこう。
\(\small{ \ \tan \ }\)の加法定理を利用する問題の中でも、この二直線のなす角を求める問題は、かなり有名な問題になるからね。
・直線と\(\small{ \ x \ }\)軸のなす角
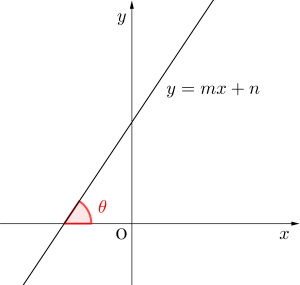
\(\small{ \ y=mx+n \ }\)と\(\small{ \ x \ }\)軸とのなす角を\(\small{ \ \theta \ }\)とするとき\(\small{ \ \tan\theta=m \ }\)
・二直線のなす角
\(\small{ \ y=m_1x+n_1 \ }\)と\(\small{ \ y=m_2x+n_2 \ }\)のなす角\(\small{ \ \theta \ }\)
\(\small{\begin{eqnarray} \ \tan\theta&=&\left|\tan\left(\theta_1-\theta_2\right)\right|\\[5pt] &=&\left|\displaystyle\frac{\tan\theta_1-\tan\theta_2}{1+\tan\theta_1\tan\theta_2}\right|\\[5pt] &=&\left|\displaystyle\frac{m_1-m_2}{1+m_1m_2}\right| \ \end{eqnarray}}\)
直線の傾きとx軸のなす角
直線\(\small{ \ y=mx+n \ }\)は傾き\(\small{ \ m \ }\)の直線だよね。
直線の傾きは\(\small{ \ y \ }\)の変化量÷\(\small{ \ x \ }\)の変化量で与えられるから、\(\small{ \ x \ }\)の変化量が\(\small{ \ 1 \ }\)のとき、\(\small{ \ y \ }\)の変化量は\(\small{ \ m \ }\)になる。
このとき直線と\(\small{ \ x \ }\)軸のなす角を\(\small{ \ \theta \ }\)とすると、\(\small{ \ \tan\theta=\displaystyle\frac{m}{1}=m \ }\)になるんだ。
つまり直線の傾きは直線と\(\small{ \ x \ }\)軸のなす角を\(\small{ \ \theta \ }\)とすると\(\small{ \ y=(\tan\theta)x+n \ }\)って書くことができるんだ。

この\(\small{ \ \tan\theta \ }\)の有名角の値は\(\small{ \ 0, \ \pm\displaystyle\frac{1}{\sqrt{3}}, \ \pm1, \ \pm\sqrt{3} \ }\)にだから、この数値の傾きの直線が出てきたら\(\small{ \ x \ }\)軸とのなす角を求めることができるってことを頭に入れておこう。
特にこのことは三角関数より、「図形と方程式」や「積分法」で円と絡めた問題に出題されることも多いからね。
加法定理を利用した二直線のなす角
\(\small{ \ x \ }\)軸と直線のなす角の正接(\(\small{ \ \tan \ }\))が傾きってことがわかったから、今度はこれを利用して二直線のなす角を求めてみよう。
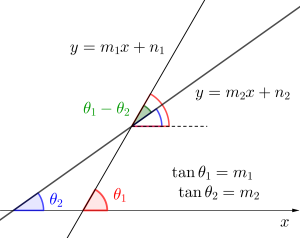
図のように二つの直線の\(\small{ \ x \ }\)軸とのなす角をそれぞれ\(\small{ \ \theta_1, \ \theta_2 \ }\)とすると二直線のなす角は\(\small{ \ \theta_1-\theta_2 \ }\)になることがわかるよね。
二つの直線の方程式が\(\small{ \ y=m_1x+n_1 \ }\)と\(\small{ \ y=m_2x+n_2 \ }\)とすると、\(\small{ \ \tan\theta_1=m_1 \ }\)、\(\small{ \ \tan\theta_2=m_2 \ }\)になるから、加法定理を利用して
\(\small{\begin{eqnarray} \ \tan\theta&=&\tan\left(\theta_1-\theta_2\right)\\[5pt]
&=&\displaystyle\frac{\tan\theta_1-\tan\theta_2}{1+\tan\theta_1\tan\theta_2}\\[5pt]
&=&\displaystyle\frac{m_1-m_2}{1+m_1m_2}\end{eqnarray} \ }\)
でなす角の正接を求めることができるんだ。

もちろん問題が「なす角を求めよ。」ってことなら、この\(\small{ \ \theta_1-\theta_2 \ }\)の値は有名角になるはずだから、もし\(\small{ \ \tan\theta=\tan\left(\theta_1-\theta_2\right) \ }\)の値が変な値になっていれば計算ミスしている可能性が高いからもう一度計算を確認しよう。
また図を見てもわかるけど、二直線のなす角の問題では直線の\(\small{ \ y \ }\)切片の値は角度に関係ないから注意しよう。
平行移動してもなす角の大きさは変わらないから\(\small{ \ y \ }\)切片は無視することが出来るんだ。

負の傾きの直線のなす角
直線の傾きが\(\small{ \ x \ }\)軸と直線のなす角の正接\(\small{ \ \tan \ }\)で与えられることがわかったけど、負の値の傾きの場合は注意が必要なんだ。
直線と\(\small{ \ x \ }\)軸のなす角は\(\small{ \ x \ }\)軸から反時計回りに回転することになるから、負の値の傾きのなす角\(\small{ \ \theta \ }\)は図の\(\small{ \ \theta_2 \ }\)のように鈍角になるから注意しよう。

二直線のなす角と絶対値
二直線のなす角って、直線が交差してるわけだから、鋭角と鈍角の二つの角があるよね。でも二直線のなす角って言われたら鋭角を答えるからね。
\(\small{ \ \tan\theta \ }\)は\(\small{ \ \theta \ }\)が鋭角だと\(\small{ \ \tan\theta\gt0 \ }\)だし、鈍角だと\(\small{ \ \tan\theta\lt0 \ }\)になるから、二直線のなす角は\(\small{ \ \tan\theta \ }\)が正になるように設定すればいいよね。
\(\small{ \ \theta \ }\)が鈍角の場合、求めるなす角は\(\small{ \ \pi-\theta \ }\)になる。
ここで、\(\small{ \ \tan\left(\pi-\theta\right)=-\tan\theta \ }\)だから、求めたなす角\(\small{ \ \theta_1-\theta_2 \ }\)が鈍角だったとき、\(\small{ \ \tan\left(\theta_1-\theta_2\right) \ }\)が負になるから、その値を正にすれば、鋭角の値の角\(\small{ \ \pi-(\theta_1-\theta_2) \ }\)がわかる。
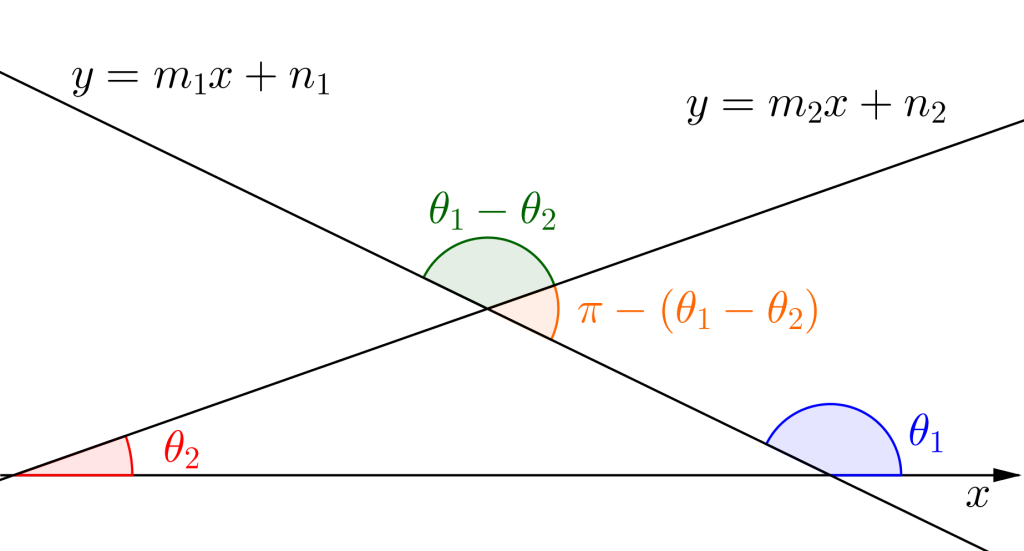
ってことは常に鋭角の値を求めたかったら、正の値を求めればいいから、\(\small{ \ \left| \tan\left(\theta_1-\theta_2\right)\right| \ }\)から角度を求めればいいんだ。
つまり\(\small{ \ y=m_1x+n_1 \ }\)と\(\small{ \ y=m_2x+n_2 \ }\)のなす角の求め方は、
\(\small{\begin{eqnarray} \ \left|\tan\theta\right|&=&\left|\tan\left(\theta_1-\theta_2\right)\right|\\[5pt]
&=&\left|\displaystyle\frac{\tan\theta_1-\tan\theta_2}{1+\tan\theta_1\tan\theta_2}\right|\\[5pt]
&=&\left|\displaystyle\frac{m_1-m_2}{1+m_1m_2}\right| \ \end{eqnarray}}\)
を計算すればいいんだ。
また、傾きが根号を含んだ複雑な式だと\(\small{ \ \theta_1 \ }\)と\(\small{ \ \theta_2 \ }\)のどっちの角が大きいか分かりにくい問題もあるよね。
でも\(\small{ \ \tan(-\theta)=-\tan\theta \ }\)だから絶対値をつけると\(\small{ \ \left|\tan(-\theta)\right|=\left|\tan\theta\right| \ }\)になって、小さいほうから大きいほうの角を引いて角度が負になっても、絶対値をつけて\(\small{ \ \tan \ }\)の値を正に書き換えることで角を求めることができるんだ。
つまり絶対値さえつけておけば、わざわざ直線の傾きの大きさを比べる必要もないんだ。
だから単純に
\(\small{\begin{eqnarray} \ \tan\theta&=&\left|\tan\left(\theta_1-\theta_2\right)\right|\\[5pt]
&=&\left|\displaystyle\frac{\tan\theta_1-\tan\theta_2}{1+\tan\theta_1\tan\theta_2}\right|\\[5pt]
&=&\left|\displaystyle\frac{m_1-m_2}{1+m_1m_2}\right| \ \end{eqnarray}}\)
に傾きを代入してしまおう。それで答えがきちんと求められるからね。
\(\small{ \ x-2y+2=0 \ }\)と\(\small{ \ 3x-y-3=0 \ }\)のなす角\(\small{ \ \theta \ }\)を求めよ。ただし、\(\small{ \ \theta \ }\)は鋭角とする。
\(\small{ \ x-2y+2=0 \ }\)を変形すると
\(\small{ \ y=\displaystyle\frac{1}{2}x+1 \ }\)
\(\small{ \ 3x-y-3=0 \ }\)を変形すると
\(\small{ \ y=3x-3 \ }\)
\(\small{ \ \tan\theta_1=\displaystyle\frac{1}{2} \ }\)、\(\small{ \ \tan\theta_2=3 \ }\)とすると
\(\small{\begin{eqnarray} \ \left|\tan\theta\right|&=&\left|\tan\left(\theta_1-\theta_2\right)\right|\\[5pt]
&=&\left|\displaystyle\frac{\tan\theta_1-\tan\theta_2}{1+\tan\theta_1\tan\theta_2}\right|\\[5pt]
&=&\left|\displaystyle\frac{\displaystyle\frac{1}{2}-3}{1+\displaystyle\frac{1}{2}\cdot3}\right|\\[5pt]
&=&1 \ \end{eqnarray}}\)
\(\small{ \ \therefore \theta=\displaystyle\frac{\pi}{4} \ }\)

Point 加法定理と二直線のなす角
①直線と\(\small{ \ x \ }\)軸とのなす角\(\small{ \ \theta \ }\)のとき、直線の傾きは\(\small{ \ \tan\theta \ }\)
⓶二直線のなす角は加法定理を利用する。

