こんにちは、リンス(@Lins016)です。
今回は3次方程式の解の個数の求め方(定数分離)について学習していこう。
定数分離と解の個数
まずは\(\small{ \ y=x^2 \ }\)と\(\small{ \ y=x+2 \ }\)の交点の求め方について考えてみよう。
まずは\(\small{ \ y \ }\)を消去して
\(\small{ \ x^2=x+2\cdots① \ }\)
\(\small{ \ x^2-x-2=0\cdots② \ }\)
\(\small{ \ (x-2)(x+1)=0 \ }\)
\(\small{ \ \therefore x=2, \ -1 \ }\)
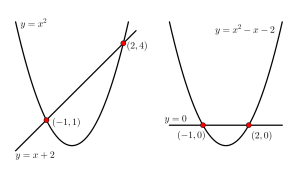
この解き方って多分全員同じことするよね。でも\(\small{ \ ① \ }\)は\(\small{ \ y=x^2 \ }\)と\(\small{ \ y=x+2 \ }\)の交点を求める式って思うけど \(\small{ \ ② \ }\)は\(\small{ \ y=x^2-x-2 \ }\)と\(\small{ \ y=0 \ }\)の交点を求める式だよね。つまりこれはどちらの交点の\(\small{ \ x \ }\)座標は\(\small{ \ x=2, \ -1 \ }\)になる。つまり式の一部を移行したものでも解の値や個数は同じになるんだ。
これを利用して、 \(\small{ \ x^3-3x^2-3x+2-a=0 \ }\)の解の個数を求める問題は\(\small{ \ x^3-3x^2-3x+2=a \ }\)と定数\(\small{ \ a \ }\)だけを移行して\(\small{ \ y=x^3-3x^2-3x+2 \ }\)と\(\small{ \ y=a \ }\)との交点を求める問題にすり替えて答えを導く。この解き方を定数分離っていうから覚えておこう。\(\small{ \ a \ }\)の値によってグラフが移動する\(\small{ \ y=x^3-3x^2-3x+2-a \ }\)と\(\small{ \ x \ }\)軸との交点を考えるより、固定された\(\small{ \ y=x^3-3x^2-3x+2 \ }\)のグラフと\(\small{ \ y=a \ }\)との交点を求める方が簡単だからね。
\(\small{ \ x \ }\)と\(\small{ \ a \ }\)を含んだ方程式\(\small{ \ g(x,a)=0 \ }\)を\(\small{ \ a=f(x) \ }\)に変形して\(\small{ \ y=a \ }\)と\(\small{ \ y=f(x) \ }\)の交点を求める。
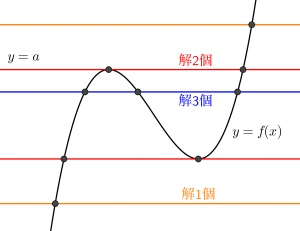
ここでポイントになるのが、この問題の解き方は定数\(\small{ \ a \ }\)が\(\small{ \ x \ }\)の係数についていない場合にだけ利用できることを覚えておこう。例えば\(\small{ \ x^3-ax+a=0 \ }\)のような形の場合、理系だと無理やり\(\small{ \ \displaystyle \frac{x^3}{x-1}=a \ }\)に変形して\(\small{ \ y=\displaystyle \frac{x^3}{x-1} \ }\)のグラフを書けばいいけど、文系の人はこのグラフは書けないから、この問題は別の方法で解いていくことになる。だからこの数学Ⅱの範囲では定数が\(\small{ \ x \ }\)の係数についていない場合だけ定数分離を利用しよう。
定数分離の解の個数と解の符号の確認
定数分離したら解の個数はグラフとの交点だから簡単に確認することができるよね。さらに一歩突っ込んでいくと、\(\small{ \ y=a \ }\)と\(\small{ \ y=f(x) \ }\)の交点の\(\small{ \ x \ }\)座標が解の値になる。解の値自体を求めることがなくても、解の正負はグラフから簡単に求めることができるからきちんと覚えておこう。よく出題される問題は「3つの解をもつとき、正の解2個、負の解1個もつときの\(\small{ \ a \ }\)の範囲を求めよ」っていうような正負の符号までを含めた問題だ。この場合\(\small{ \ x \ }\)軸正の位置で2点、負の位置で1点交われば良いので\(\small{ \ f(0) \ }\)の値を調べ、そこを境に範囲が変化することに注意しよう。こんな問題の場合、\(\small{ \ a=f(0) \ }\)のとき、正の解、負の解、\(\small{ \ x=0 \ }\)になる場合がほとんどだから、グラフをかいて確認しよう。
3次方程式\(\small{ \ x^3-3x+1+a=0 \ }\)について次の問いに答えよ。
(1)異なる実数解を2個持つときの\(\small{ \ a \ }\)の値を求めよ。
(2)正の解2個と負の解1個持つときの\(\small{ \ a \ }\)の範囲を求めよ。
\(\small{ \ x^3-3x+1+a=0 \ }\)を変形して
\(\small{ \ a=-x^3+3x-1 \ }\)
\(\small{ \ f(x)=-x^3+3x-1 \ }\)とすると
\(\small{ \ f'(x)=-3x^2+3=-3(x-1)(x+1) \ }\)
増減表を書くと
\(\small{ \ \begin{array}{c|ccccc}
x & \cdots & -1 & \cdots & 1 & \cdots \\
\hline
f’(x) & - & 0 & + & 0 & - \\
\hline
f(x) & \searrow & -3 & \nearrow & 1 & \searrow
\end{array} \ }\)
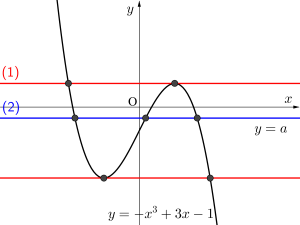
(1)グラフより
\(\small{ \ a=-3, \ 1 \ }\)
(2)\(\small{ \ y=-x^3+3x-1 \ }\)と\(\small{ \ y=a \ }\)のグラフの交点の\(\small{ \ x \ }\)座標が正の部分で2個負の部分で1個交わればよい。
\(\small{ \ f(0)=-1 \ }\)より
\(\small{ \ -1 \lt a \lt 1 \ }\)

Point
①\(\small{ \ a=f(x) \ }\)の形に定数分離
②交点の座標の位置で正の解、負の解を判定
\(\small{ \ x^3-6x^2+9x+1-a=0 \ }\)が異なる\(\small{ \ 3 \ }\)つの実数解\(\small{ \ \alpha, \ \beta, \ \gamma \ (\alpha \lt \beta \lt \gamma) \ }\)をもつとき、\(\small{ \ a \ }\)の範囲とそれぞれの実数解の値の範囲を求めよ。
\(\small{ \ a=x^3-6x^2+9x+1 \ }\)
\(\small{ \ f(x)=x^3-6x^2+9x+1 \ }\)とすると
\(\small{ \ f'(x)=3x^2-12x+9=3(x-1)(x-3) \ }\)より
増減表は
\(\small{ \ \begin{array}{c|ccccc}
x & \cdots & 1 & \cdots & 3 & \cdots \\
\hline
f’(x) & - & 0 & + & 0 & - \\
\hline
f(x) & \nearrow & 5 & \searrow & 1 & \nearrow
\end{array} \ }\)
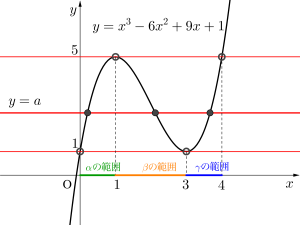
よってグラフより異なる\(\small{ \ 3 \ }\)つの解をもつのは\(\small{ \ 1 \lt a \lt 5 \ }\)
また\(\small{ \ f(x)=f(1) \ }\)とすると
\(\small{ \ x^3-6x^2+9x-4=0 \ }\)
\(\small{ \ (x-1)^2(x-4)=0 \ }\)
\(\small{ \ \therefore x=1, \ 4 \ }\)
また\(\small{ \ f(x)=f(3) \ }\)とすると
\(\small{ \ x^3-6x^2+9x=0 \ }\)
\(\small{ \ x(x-3)^2=0 \ }\)
\(\small{ \ \therefore x=0, \ 3 \ }\)
よってグラフより求める範囲は
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
0 \lt \alpha \lt 1\\
1 \lt \beta \lt 3\\
3 \lt \gamma \lt 4
\end{array}
\right.
\end{eqnarray} \ }\)

