こんにちは、リンス(@Lins016)です。
今回は3次関数の最大最小の基本について学習していこう。
3次関数の最大最小
3次関数って\(\small{ \ x \ }\)がすべての実数の範囲を動くとき、最大値も最小値も存在しない。だって\(\small{ \ x \ }\)が\(\small{ \ \infty \ }\)に動くと\(\small{ \ y \ }\)も\(\small{ \ \infty \ }\)や\(\small{ \ -\infty \ }\)に動くからね。ってことは最大最小が存在する条件は\(\small{ \ x \ }\)に範囲が存在するってことになる。ちなみにこの範囲のことを定義域っていうよね。3次関数の最大最小を考えるときは必ず定義域について考えるようにしよう。
定義域がない場合

定義域が存在する場合
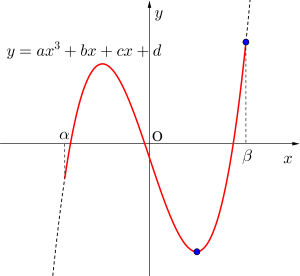
定義域が与えられた3次関数の最大最小
定義域が与えられた問題は3次関数の最大最小の基本中の基本。増減表を書いてグラフから最大最小を調べよう。注意するところは極大値・極小値が最大値・最小値になるわけじゃないってことだよね。グラフの端の値をきちんと求め、極大値極小値との値を比較しよう。
次の関数の最大値と最小値を求めよ。
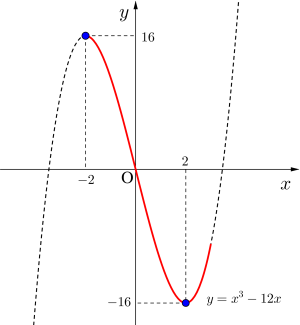
(1)\(\small{ \ y=x^3-12x \ (-2 \leqq \ x \ \leqq 3) \ }\)
\(\small{ \ y=x^3-12x \ }\)
\(\small{ \ \begin{eqnarray}y'&=&3x^2-12\\
&=&3(x+2)(x-2)\end{eqnarray} \ }\)
よって増減表を書くと
\(\small{ \ \begin{array}{c|ccccc}
x & -2 & \cdots & 2& \cdots & 3 \\
\hline
y'& 0 & - & 0 & + & \\
\hline
y & 16 & \searrow & -16 & \nearrow & -9
\end{array}
\ }\)
よって最大値\(\small{ \ 16 \ (x=-2) \ }\)
最小値\(\small{ \ -16 \ (x=2) \ }\)
定義域を求める3次関数の最大最小
今度は与えられた条件式から定義域を求める3次関数の最大最小になる。定義域を求めてしまえば、定義域が与えられた3次関数の最大最小と同じだから、定義域を求めることが非常に重要になるよね。
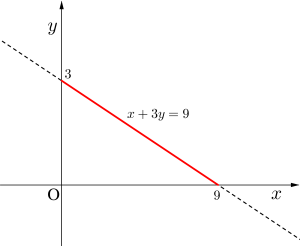
\(\small{ \ x+3y=9, \ x\geqq0, \ y\geqq0 \ }\)のとき\(\small{ \ x^2y \ }\)の最大値と最小値を求めよ。
\(\small{ \ x+3y=9 \ }\)より\(\small{ \ x=9-3y \ }\)
\(\small{ \ x\geqq0 \ }\)より\(\small{ \ 9-3y \geqq 0 \ }\)
\(\small{ \ \therefore 0 \leqq y \leqq 3 \ }\)
\(\small{ \ \begin{eqnarray}x^2y&=&(9-3y)^2y\\
&=&9y^3-54y^2+81y\end{eqnarray} \ }\)
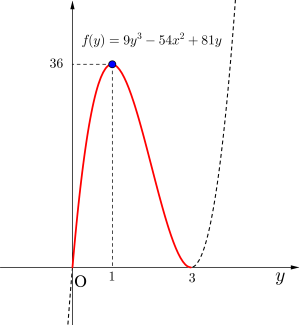
\(\small{ \ f(y)=9y^3-54y^2+81y \ }\)とすると
\(\small{\begin{eqnarray}f'(y)&=&27y^2-108y+81\\
&=&27(y-1)(y-3) \ \end{eqnarray}}\)
よって増減表を書くと
\(\small{ \ \begin{array}{c|ccccc}
y & 0 & \cdots & 1 & \cdots & 3 \\
\hline
f'(y)& & + & 0 & 1 & 0 \\
\hline
f(y) & 0 & \nearrow & 36 & \searrow & 0
\end{array}
\ }\)
よって最大値\(\small{ \ 36 \ (x=6, \ y=1) \ }\)
最小値\(\small{ \ 0 \ (x=9, \ y=0), \ (x=0, \ y=3) \ }\)

Point
①3次関数の最大最小は定義域が存在する
②極大値極小値が最大最小になるとは限らない
\(\small{ \ x \ }\)が\(\small{ \ 0 \leqq x \lt 2\pi \ }\)の範囲を動くとき、\(\small{ \ \sin x+\cos x =t \ }\)とおいて、\(\small{ \ \sin^3 x+\cos^3 x \ }\)の最大値と最小値とそのときの\(\small{ \ t \ }\)の値を求めよ。
\(\small{\begin{eqnarray} \ t&=&\sin x+\cos x\\
&=&\sqrt{2}\left( \displaystyle \frac{1}{\sqrt{2}}\sin x+\displaystyle \frac{1}{\sqrt{2}}\cos x\right)\\
&=&\sqrt{2}\sin\left(x+\displaystyle \frac{\pi}{4}\right) \ \end{eqnarray}}\)
\(\small{ \ 0 \leqq x \lt 2\pi \ }\)より\(\small{ \ -\sqrt{2} \leqq t \leqq \sqrt{2} \ }\)
\(\small{ \ t=\sin x + \cos x \ }\)より
\(\small{ \ t^2=1+2\sin x \cos x \ }\)
\(\small{ \ \sin^3 x+\cos^3 x \ }\)
\(\small{\begin{eqnarray} &=&(\sin x+\cos x)^3-3\sin x \cos x(\sin x+\cos x)\\
&=&t^3-3\displaystyle \frac{t^2-1}{2}t \\
&=&-\displaystyle \frac{1}{2}t^3+\displaystyle \frac{3}{2}t \ \end{eqnarray}}\)
\(\small{ \ f(t)= -\displaystyle \frac{1}{2}t^3+\displaystyle \frac{3}{2}t\ }\)とすると
\(\small{ \ f'(t)=-\displaystyle \frac{3}{2}(t+1)(t-1) \ }\)
\(\small{ \
\begin{array}{c|ccccc}
x & -\sqrt{2} &\cdots & -1 & \cdots & 1 & \cdots & \sqrt{2}\\
\hline
f’(x) & & - & 0 & + & 0 & - & \\
\hline
f(x) & -\displaystyle \frac{\sqrt{2}}{2} & \searrow & -1 & \nearrow & 1 & \searrow & \displaystyle \frac{\sqrt{2}}{2}
\end{array} \ }\)
よって最大値\(\small{ \ 1 \ (t=1) \ }\)
最大値\(\small{ \ -1 \ (t=-1) \ }\)

