こんにちは、リンス(@Lins016)です。
今回は三次関数の点対称の証明について学習していこう。
\(\small{ \ f(x)=ax^3+bx^2+cx+d \ }\)のグラフは
変曲点\(\small{ \ \left(-\displaystyle \frac{b}{3a}, \ \displaystyle \frac{2b^3}{27a^2}-\displaystyle \frac{bc}{3a}+d \right) \ }\)に関して対称である
変曲点とは平面上の曲線で曲がる方向が変わる点(グラフの凸が変化する点)のことで三次関数では\(\small{ \ f''(x)=0 \ }\)を満たす点
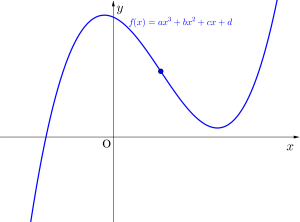
\(\small{ \ f(x)=ax^3+bx^2+cx+d \ }\)
\(\small{ \ f'(x)=3ax^2+2bx+c \ }\)
\(\small{ \ f''(x)=6ax+2b \ }\)
\(\small{ \ f''(x)=0 \ }\)とすると\(\small{ \ x=-\displaystyle \frac{b}{3a} \ }\)
\(\small{ \ f\left(-\displaystyle \frac{b}{3a}\right)=\displaystyle \frac{2b^3}{27a^2}-\displaystyle \frac{bc}{3a}+d \ }\)
よって変曲点は\(\small{ \ \left(-\displaystyle \frac{b}{3a}, \ \displaystyle \frac{2b^3}{27a^2}-\displaystyle \frac{bc}{3a}+d \right) \ }\)
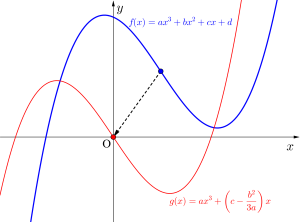
ここで変曲点が原点に移動するように平行移動すると平行移動した式は
これを整理すると
\(\small{ \ y=ax^3+\left(c-\displaystyle \frac{b^2}{3a}\right)x \ }\)となる
\(\small{ \ g(x)=ax^3+\left(c-\displaystyle \frac{b^2}{3a}\right)x \ }\)とすると
\(\small{\begin{eqnarray} \ g(-x)&=&a(-x)^3+\left(c-\displaystyle \frac{b^2}{3a}\right)(-x)\\
&=&-ax^3-\left(c-\displaystyle \frac{b^2}{3a}\right)x\\
&=&-g(x) \ \end{eqnarray}}\)
\(\small{ \ g(-x)=-g(x) \ }\)より\(\small{ \ y=g(x) \ }\)は奇関数となり原点対称である
よって\(\small{ \ f(x)=ax^3+bx^2+cx+d \ }\)は変曲点に関して対称なグラフである

