こんにちは、リンス(@Lins016)です。
今回はトレミーの定理の証明について学習していこう。
トレミーの定理とその証明
円に内接する四角形\(\small{ \ \mathrm{ABCD} \ }\)において
\(\small{ \ \mathrm{AB}\cdot \mathrm{CD}+\mathrm{BC}\cdot \mathrm{AD}=\mathrm{AC}\cdot \mathrm{BD} \ }\)
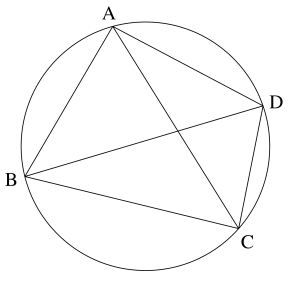
相似を利用したトレミーの定理の証明
\(\small{ \ \angle \mathrm{BAD} \ }\)内に\(\small{ \ \angle \mathrm{BAE}= \angle \mathrm{CAD} \ }\)となるように\(\small{ \ \mathrm{BD} \ }\)上に点\(\small{ \ \mathrm{E} \ }\)をとる。
\(\small{ \ \triangle \mathrm{ABE} \ }\)と\(\small{ \ \triangle \mathrm{ACD} \ }\)において
仮定より\(\small{ \ \angle \mathrm{BAE}= \angle \mathrm{CAD} \ }\)
\(\small{ \ \stackrel{\Large \frown}{\mathrm{AD}} \ }\)に対する円周角より
\(\small{ \ \angle \mathrm{ABE}= \angle \mathrm{ACD} \ }\)
\(\small{ \ 2 \ }\)つの角がそれぞれ等しいので
\(\small{ \ \triangle \mathrm{ABE}\backsim \triangle \mathrm{ACD}\cdots① \ }\)

\(\small{ \ \triangle \mathrm{ABC} \ }\)と\(\small{ \ \triangle \mathrm{AED} \ }\)において
仮定より\(\small{ \ \angle \mathrm{BAE}= \angle \mathrm{CAD} \ }\)
\(\small{ \ \angle \mathrm{BAC}= \angle \mathrm{BAE}+ \angle \mathrm{EAC} \ }\)
\(\small{ \ \angle \mathrm{EAD}= \angle \mathrm{DAC}+ \angle \mathrm{EAC} \ }\)
\(\small{ \ \therefore \angle \mathrm{BAC}= \angle \mathrm{EAD} \ }\)
\(\small{ \ \stackrel{\Large \frown}{\mathrm{AB}} \ }\)に対する円周角より
\(\small{ \ \angle \mathrm{ACB}= \angle \mathrm{ADE} \ }\)
よって\(\small{ \ 2 \ }\)つの角がそれぞれ等しいので
\(\small{ \ \triangle \mathrm{ABC}\backsim \triangle \mathrm{AED}\cdots② \ }\)
\(\small{ \ ①}\)より\(\small{ \ \mathrm{AB}: \mathrm{AC}= \mathrm{BE}: \mathrm{CD} \ }\)
\(\small{ \ \therefore \mathrm{AB}\cdot \mathrm{CD}= \mathrm{AC}\cdot \mathrm{BE} \ }\)
\(\small{ \ ②}\)より\(\small{ \ \mathrm{BC}: \mathrm{DE}= \mathrm{AC}: \mathrm{AD}\cdots③ \ }\)
\(\small{ \ \therefore \mathrm{BC}\cdot \mathrm{AD}= \mathrm{AC}\cdot \mathrm{DE}\cdots④ \ }\)
\(\small{ \ ③+④ \ }\)より
\(\small{ \ \mathrm{AB}\cdot \mathrm{CD}+\mathrm{BC}\cdot \mathrm{AD}=\mathrm{AC}\cdot \mathrm{BE}+\mathrm{AC}\cdot \mathrm{DE} \ }\)
\(\small{ \ \therefore \mathrm{AB}\cdot \mathrm{CD}+\mathrm{BC}\cdot \mathrm{AD}=\mathrm{AC}\cdot \mathrm{BD} \ }\)
余弦定理を利用したトレミーの定理の証明
\(\small{ \ \triangle \mathrm{ABD} \ }\)に余弦定理を適用して
\(\small{ \ \cos \mathrm{A}=\displaystyle \frac{\mathrm{AB}^2+ \mathrm{AD}^2- \mathrm{BD}^2}{2 \mathrm{AB}\cdot \mathrm{AD}} \ }\)
\(\small{ \ \triangle \mathrm{ABC} \ }\)に余弦定理を適用して
\(\small{ \ \cos \mathrm{B}=\displaystyle \frac{\mathrm{AB}^2+ \mathrm{BC}^2- \mathrm{AC}^2}{2 \mathrm{AB}\cdot \mathrm{BC}} \ }\)
\(\small{ \ \triangle \mathrm{BCD} \ }\)に余弦定理を適用して
\(\small{ \ \cos \mathrm{C}=\displaystyle \frac{\mathrm{BC}^2+ \mathrm{CD}^2- \mathrm{BD}^2}{2 \mathrm{BC}\cdot \mathrm{CD}} \ }\)
\(\small{ \ \triangle \mathrm{ACD} \ }\)に余弦定理を適用して
\(\small{ \ \cos \mathrm{D}=\displaystyle \frac{\mathrm{AD}^2+ \mathrm{CD}^2- \mathrm{AC}^2}{2 \mathrm{AD}\cdot \mathrm{CD}} \ }\)
ここで四角形\(\small{ \ \mathrm{ABCD} \ }\)は円に内接しているので
\(\small{ \ \angle \mathrm{A}+ \angle \mathrm{C}=180^{\circ} \ }\)、\(\small{ \ \angle \mathrm{B}+ \angle \mathrm{D}=180^{\circ} \ }\)
\(\small{ \ \therefore \cos \mathrm{A}=-\cos \mathrm{C} \ }\)、\(\small{ \ \therefore \cos \mathrm{B}=-\cos \mathrm{D} \ }\)
\(\small{ \ \displaystyle \frac{\mathrm{AB}^2+ \mathrm{AD}^2- \mathrm{BD}^2}{2 \mathrm{AB}\cdot \mathrm{AD}}=-\displaystyle \frac{\mathrm{BC}^2+ \mathrm{CD}^2- \mathrm{BD}^2}{2 \mathrm{BC}\cdot \mathrm{CD}} \ }\)
\(\small{ \ \displaystyle \frac{\mathrm{AB}^2+ \mathrm{BC}^2- \mathrm{AC}^2}{2 \mathrm{AB}\cdot \mathrm{BC}}=-\displaystyle \frac{\mathrm{AD}^2+ \mathrm{CD}^2- \mathrm{AC}^2}{2 \mathrm{AD}\cdot \mathrm{CD}} \ }\)
\(\small{ \ ①② \ }\)をかけ合わせて整理すると
\(\small{ \ \mathrm{AC}^2 \cdot \mathrm{BD}^2=(\mathrm{AB}\cdot \mathrm{CD}+ \mathrm{BC}\cdot \mathrm{AD})^2 \ }\)
\(\small{ \ \therefore \mathrm{AC} \cdot \mathrm{BD}=\mathrm{AB}\cdot \mathrm{CD}+ \mathrm{BC}\cdot \mathrm{AD} \ }\)


