こんにちは、リンス(@Lins016)です。
今回は特殊な三角比の値について学習していこう。
有名角以外の三角比
有名角の三角比の値は、さすがに全部覚えてるよね?これ覚えてなかったら0点だからね。絶対覚えてね。そしてさらに、今回学習する特殊な三角比の値についても覚えていてほしい。
だってこれ知ってるのと知らないのじゃ、定期テストレベルだと問題ないかもしれないけど、入試レベルだと差がつくことになるからね。
\(\small{ \ \sin15^{\circ}=\displaystyle \frac{\sqrt{6}-\sqrt{2}}{4} \ }\)
\(\small{ \ \cos15^{\circ}=\displaystyle \frac{\sqrt{6}+\sqrt{2}}{4} \ }\)
\(\small{ \ \tan15^{\circ}=2-\sqrt{3} \ }\)
\(\small{ \ \sin75^{\circ}=\displaystyle \frac{\sqrt{6}+\sqrt{2}}{4} \ }\)
\(\small{ \ \cos75^{\circ}=\displaystyle \frac{\sqrt{6}-\sqrt{2}}{4} \ }\)
\(\small{ \ \tan75^{\circ}=2+\sqrt{3} \ }\)
\(\small{ \ \cos36^{\circ}=\displaystyle \frac{1+\sqrt{5}}{4} \ }\)
15度・75度の三角比
有名角は30度、45度、60度、90度・・・っていうように15度間隔の部分と30度間隔の部分があるから、15度、75度の値を覚えてしまえば、15度間隔で三角比を答えることができるよね。
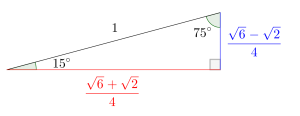
ちなみに受験生であれば、この値は当然知ってないといけないからね。覚えていない人はきちんと覚えておこう。
図の三角形を単位円に当てはめることで105度、165度の三角比も答えることができるからね。
図の三角形の\(\small{ \ \mathrm{AB}=1 \ }\)として、\(\small{ \ \tan15^{\circ} \ }\)を求めよ。
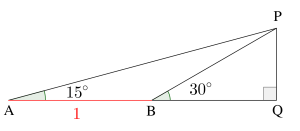
\(\small{ \ \angle\mathrm{APB}+\angle\mathrm{PAB}=\angle \mathrm{PBQ} \ }\)より
\(\small{ \ \angle \mathrm{APB}=15^{\circ} \ }\)
よって\(\small{ \ \triangle \mathrm{ABP} \ }\)は二等辺三角形より\(\small{ \ \mathrm{BP}=1 \ }\)
\(\small{ \ \mathrm{PQ}=\mathrm{BP}\sin30^{\circ}=\displaystyle \frac{1}{2} \ }\)
\(\small{ \ \mathrm{BQ}=\mathrm{BP}\cos30^{\circ}=\displaystyle \frac{\sqrt{3}}{2} \ }\)
\(\small{\begin{eqnarray} \ \tan 15^{\circ}&=&\displaystyle \frac{\mathrm{AQ}}{\mathrm{PQ}}=\displaystyle \frac{\displaystyle \frac{1}{2}}{1+\displaystyle \frac{\sqrt{3}}{2}}\\[10pt]
&=&\displaystyle \frac{1}{2+\sqrt{3}}=2-\sqrt{3} \ \end{eqnarray}}\)


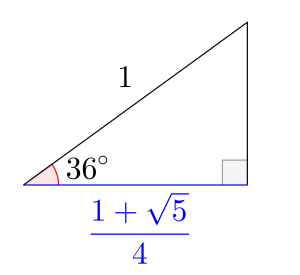
36度の三角比
\(\small{ \ \cos36^{\circ}=\displaystyle \frac{1+\sqrt{5}}{4} \ }\)って値なんだけど、これを2倍すると\(\small{ \ 2\cos36^{\circ}=\displaystyle \frac{1+\sqrt{5}}{2} \ }\)ってなって、この値は黄金比って呼ばれている値で、人間にとって最も美しい比率って言われたりしている比の値なんだ。
この比を取り入れることでデザインがよく見えたりするから、写真の構図など様々なものに取り入れられてるみたいだから、気になる人は調べてみるといい。
有名なところだと「モナリザ」や「ミロのビーナス」なんかにも取り入れらてるって言われてるからね。
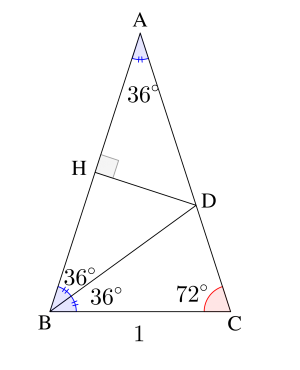
\(\small{ \ \triangle \mathrm{ABC} \ }\)において\(\small{ \ \angle \mathrm{B}=\angle \mathrm{C}=72^{\circ} \ }\)、\(\small{ \ \mathrm{BC}=1 \ }\)であり、\(\small{ \ \angle \mathrm{B} \ }\)の二等分線と辺\(\small{ \ \mathrm{AC} \ }\)との交点を\(\small{ \ \mathrm{D} \ }\)とする。
(1)\(\small{ \ \mathrm{CD} \ }\)の長さを求めよ。
(2)\(\small{ \ \cos36^{\circ} \ }\)を求めよ。
(1)\(\small{ \ \angle \mathrm{ABD}=\angle\mathrm{CBD} =36^{\circ}\ }\)より
\(\small{ \ \angle\mathrm{BDC}=180^{\circ}-(36^{\circ}+72^{\circ})=72^{\circ} \ }\)
よって\(\small{ \ \angle\mathrm{BDC}=\angle\mathrm{BCD}=72^{\circ} \ }\)
また\(\small{ \ \angle \mathrm{DAB}=\angle \mathrm{DBA}=36^{\circ} \ }\)
つまり\(\small{ \ \triangle \mathrm{DAB} \ }\)と\(\small{ \ \triangle \mathrm{BCD} \ }\)はいずれも二等辺三角形
よって\(\small{ \ \mathrm{AD}=\mathrm{BD}=\mathrm{BC}=1 \ }\)
また\(\small{ \ \triangle \mathrm{ABC}\backsim \triangle \mathrm{BCD} \ }\)より
\(\small{ \ \displaystyle \frac{\mathrm{AB}}{\mathrm{BC}}=\displaystyle \frac{\mathrm{BC}}{\mathrm{CD}} \ }\)が成り立つ
\(\small{ \ \mathrm{CD}=x \ }\)とすると
\(\small{ \ \displaystyle \frac{1+x}{1}=\displaystyle \frac{1}{x} \ }\)
\(\small{ \ x^2+x-1=0 \ }\)
\(\small{ \ x\gt0 \ }\)より\(\small{ \ x=\displaystyle \frac{-1+\sqrt{5}}{4} \ }\)
(2) \(\small{ \ \mathrm{D} \ }\)より辺\(\small{ \ \mathrm{AB} \ }\)に下ろした垂線の足を\(\small{ \ \mathrm{H} \ }\)とすると
\(\small{ \ \mathrm{AH}=\displaystyle \frac{1}{2}\mathrm{AB}=\displaystyle \frac{1+\sqrt{5}}{4} \ }\)
\(\small{ \ \cos36^{\circ}=\displaystyle \frac{\mathrm{AH}}{\mathrm{AD}}=\displaystyle \frac{1+\sqrt{5}}{4} \ }\)

Point 特殊な三角比の値
①15°、75°の三角比の値は覚えておこう
②図形から三角比を求めることができることを知っておこう

