こんにちは、リンス(@Lins016)です。
今回は解と係数の関係について学習していこう。
解と係数の関係の利用
解と係数の関係はこの「複素数と方程式」以外の他の単元でも利用することが多い。
だから今回勉強してきちんと押さえておこう。
\(\small{ \ ax^2+bx+c=0 \ }\)の解を\(\small{ \ x=\alpha, \ \beta \ }\)とすると
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
\alpha+\beta=-\displaystyle\frac{b}{a}\\
\alpha\beta=\displaystyle\frac{c}{a}
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ ax^3+bx^2+cx+d=0 \ }\)の解を\(\small{ \ \alpha \ }\)、\(\small{ \ \beta\ }\)、\(\small{ \ \gamma \ }\)とすると
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
\alpha+\beta+\gamma=-\displaystyle \frac{b}{a}\\
\alpha\beta+\beta\gamma+\gamma\alpha=\displaystyle \frac{c}{a}\\
\alpha\beta\gamma=-\displaystyle \frac{d}{a}
\end{array}
\right.
\end{eqnarray} \ }\)
まずは解と係数の関係の証明を確認しておこう。
-

解と係数の関係の証明
二次方程式と三次方程式の解と係数の関係の証明について詳しく解説しています。
続きを見る
解と係数の関係の利用
解と係数の関係は「方程式の係数」と「方程式の解」の関係式で、二次方程式だけじゃなく実数係数の高次方程式で利用することができるんだ。
でも実際に入試に出題されるのは二次方程式と三次方程式の解と係数の関係だからこの二つの関係式をしっかりと押さえておこう。
あと解と係数の関係から方程式を作成させる問題も定期試験によく出題されるからきちんと確認しておこう。
(1)\(\small{ \ 2 \ }\)次方程式\(\small{ \ x^2+px+8=0 \ }\)の\(\small{ \ 2 \ }\)つの解の差が\(\small{ \ 3 \ }\)であるとき、実数の定数\(\small{ \ p \ }\)の値を求めよ。
(2)\(\small{ \ 2 \ }\)次方程式\(\small{ \ x^2-p^2x-p=0 \ }\)の2つの解は\(\small{ \ x^2+px-1=0 \ }\)の\(\small{ \ 2 \ }\)つの解に、それぞれ\(\small{ \ 1 \ }\)を加えたものに等しいという。実数の定数\(\small{ \ p \ }\)の値を求めよ。
(1)\(\small{ \ 2 \ }\)次方程式\(\small{ \ x^2+px+8=0 \ }\)の解は\(\small{ \ \alpha \ }\)と\(\small{ \ \alpha+3 \ }\)とおける
解と係数の関係より
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
\alpha+\alpha +3=-p\\
\alpha (\alpha +3)=8
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ \alpha^2+3\alpha-8=0 \ }\)
\(\small{ \ \therefore \alpha=\displaystyle \frac{-3\pm\sqrt{3^2+32}}{2}=\displaystyle \frac{-3\pm\sqrt{41}}{2} \ }\)
\(\small{ \ p=2\alpha+3=\pm\sqrt{41} \ }\)
(2)\(\small{ \ x^2+px-1=0 \ }\)の解を\(\small{ \ x=\alpha, \ \beta \ }\)とする
解と係数の関係より
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
\alpha+\beta=-p\cdots①\\
\alpha\beta=-1\cdots②
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ x^2-p^2x-p=0 \ }\)の解は\(\small{ \ x=\alpha+1, \ \beta+1 \ }\)となるので
解と係数の関係より
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
\alpha+\beta+2=p^2\cdots③\\
(\alpha+1)(\beta+1)=-p\cdots④
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{①, \ ③ }\)より
\(\small{ \ p^2-2=-p \ }\)
\(\small{ \ p^2+p-2=0 \ }\)
\(\small{ \ (p+2)(p-1)=0 \ }\)
\(\small{ \ \therefore p=-2, \ 1 \ }\)
これは\(\small{ ②, \ ④ }\)も満たす。
よって\(\small{ \ p=-2, \ 1 \ }\)

方程式が二つ与えらえてる場合は、どっちの解を基準にするのか問題文から正確に読み取ろう。
解と係数の関係と対称式
解と係数の関係は対称式としてもよく利用される。
「対称式って何?」って人はもう一度復習しておこう。
-

対称式
基本対称式の解説や定番の対称式を解説しています。
続きを見る
学校の定期試験でも大学入試問題でも解と係数の関係を利用する場合は、対称式になっているから求めたい値の式を基本対称式で表そう。
\(\small{ \ 2x^2-4x+1=0 \ }\)の解を\(\small{ \ x=\alpha, \ \beta \ }\)とするとき、次の式の値を求めよ。
(1)\(\small{ \ \alpha^2\beta+\alpha\beta^2 \ }\)
(2)\(\small{ \ (\alpha-\beta)^2 \ }\)
(3)\(\small{ \ \alpha^3+\beta^3 \ }\)
(4)\(\small{ \ \displaystyle\frac{\alpha^2}{\beta}+\displaystyle\frac{\beta^2}{\alpha} \ }\)
\(\small{ \ \alpha+\beta=2 \ }\)
\(\small{ \ \alpha\beta=\displaystyle\frac{1}{2} \ }\)
(1)
\(\small{\begin{eqnarray} \ \alpha^2\beta+\alpha\beta^2&=&\alpha\beta(\alpha+\beta)\\
&=&\displaystyle\frac{1}{2}\cdot2\\
&=&1 \ \end{eqnarray}}\)
(2)
\(\small{\begin{eqnarray} \ (\alpha-\beta)^2&=&(\alpha+\beta)^2-4\alpha\beta\\
&=&2^2-4\cdot\displaystyle\frac{1}{2}\\
&=&2 \ \end{eqnarray}}\)
(3)
\(\small{\begin{eqnarray} \ \alpha^3+\beta^3&=&(\alpha+\beta)^3-3\alpha\beta(\alpha+\beta)\\
&=&2^3-3\cdot\displaystyle\frac{1}{2}\cdot2\\
&=&5 \ \end{eqnarray}}\)
(4)
\(\small{ \begin{eqnarray}\ \displaystyle\frac{\alpha^2}{\beta}+\displaystyle\frac{\beta^2}{\alpha}&=&\displaystyle\frac{\alpha^3+\beta^3}{\alpha\beta}\\
&=&5\cdot2\\
&=&10 \ \end{eqnarray}}\)

解と係数の関係をいつ使うか?
定期試験で「複素数と方程式」の単元が試験範囲なら問題文に「解を\(\small{ \ \alpha, \ \beta \ }\)とする」って書いてある問題もあって、解と係数の関係を利用するんだってすぐわかるよね。
でも大学入試や実力試験では「解を\(\small{ \ \alpha, \ \beta \ }\)とする」って書いてある問題はほとんどなくて、自分で解を\(\small{ \ \alpha, \ \beta \ }\)っておいて問題を解き進めていかないといけないんだ。
今回はそのことを踏まえて解と係数の関係をいつ利用するのかってことを少し考えてみよう。
例えば\(\small{ \ x^2-2x-8=0 \ }\)の解は\(\small{ \ x=4, \ -2 \ }\)だよね。
これだと解と係数の関係を利用しなくても直接解を代入したほうが計算も楽で早そうだよね。
それに対して\(\small{ \ x^2-ax+3a=0 \ }\)の解は\(\small{ \ x=\displaystyle\frac{a\pm\sqrt{a^2-12a}}{2} \ }\)になるから、この解を毎回式に記入するのはそれだけでも手間だよね。
しかも途中で書き間違いとかしそうだしね。
こういう場合に解と係数の関係というか解を\(\small{ \ \alpha, \ \beta \ }\)とおいて、毎回\(\small{ \ \displaystyle\frac{a\pm\sqrt{a^2-12a}}{2} \ }\)って書くのを省略するんだ。
そうすることで式も簡単にかけるよね。
そして問題文にもよるんだけど、計算している式や求めてる値は\(\small{ \ \alpha, \ \beta \ }\)って書いたまま進めていくと、解と係数の関係が利用できる形になる場合が多い。
本当は解の公式を使って複雑な式のまま書き進めても答えは出せるんだ。
だけど、\(\small{ \ \alpha, \ \beta \ }\)っておくことで書くのも簡単になって、さらに解と係数の関係を利用することにも気付けるから、より簡単に計算することができるんだ。
つまり方程式の解が複雑な問題では解を\(\small{ \ \alpha, \ \beta \ }\)として解くほうがいいんだ。
特に数学Ⅱの微分法や積分法や図形と方程式とかでよく使われるから、方程式の解が複雑な場合は解を\(\small{ \ \alpha, \ \beta \ }\)とおいて、解と係数の関係が使えるかもって思いながら問題を解き進めよう。
-

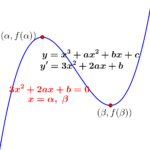
三次関数の極大値・極小値(極値)と解と係数の関係
解と係数の関係から対称式の利用まで詳しく解説しています。
続きを見る
-

円と直線の共有点
こんにちは、リンス(@Lins016)です。 今回は円と直線の共有点について学習していこう。 円と直線の位置関係 円と直線の位置関係によって\(\small{ \ 2 \ }\)点で交わる、接する、交 ...
続きを見る
-

媒介変数で表された軌跡の方程式
媒介変数で表された軌跡の求め方について詳しく解説しています。
続きを見る
Point 解と係数の関係
①解が複雑な式は解を\(\small{ \ \alpha, \ \beta \ }\)とおこう
②二次方程式や三次方程式では解と係数の関係を常に意識しておこう。
\(\small{ \ x \ }\)についての\(\small{ \ 3 \ }\)次方程式\(\small{ \ f(x)=0 \ }\)の\(\small{ \ 3 \ }\)つの解を\(\small{ \ \alpha, \ \beta, \ \gamma \ }\)とするとき、\(\small{ \ f(x) \ }\)と\(\small{ \ \alpha, \ \beta, \ \gamma \ }\)は次の条件を満たしている。
(A)\(\small{ \ f(0)=6 \ }\)
(B)\(\small{ \ f(x)-f(-x)=9x^3-18x \ }\)
(C)\(\small{ \ \alpha+\beta+\gamma=3 \ }\)
(1)\(\small{ \ \alpha\beta+\beta\gamma+\gamma\alpha \ }\)を求めよ。
(2)\(\small{ \ \alpha^2+\beta^2+\gamma^2 \ }\)の値を求めよ。
(3)\(\small{ \ \alpha^3+\beta^3+\gamma^3 \ }\)の値を求めよ。
(A)(C) より
\(\small{ \ f(x)=ax^3-3ax^2+bx+6 \ }\)とおける。ただし\(\small{ \ a\neq0 \ }\)
(B)より
\(\small{ \ f(x)-f(-x)=2ax^3+2bx=9x^3-18x \ }\)
よって\(\small{ \ a=\displaystyle \frac{9}{2}, \ b=-9 \ }\)
\(\small{ \ \therefore \ f(x)=\displaystyle \frac{9}{2}x^3-\displaystyle \frac{27}{2}x^2-9x+6 \ }\)
(1)解と係数の関係より
\(\small{ \ \alpha\beta+\beta\gamma+\gamma\alpha=\displaystyle \frac{b}{a}=-2 \ }\)
(2)
&=&3^2-2(-2)\\
&=&13 \ \end{eqnarray}}\)
(3)
&=&3\cdot\left\{13-(-2)\right\}+3\cdot(-6)\cdot\displaystyle \frac{2}{9}\\
&=&41 \ \end{eqnarray}}\)

&=&(\alpha+\beta+\gamma)(\alpha^2+\beta^2+\gamma^2-\alpha\beta-\beta\gamma-\gamma\alpha) \ \end{eqnarray}}\)
だよね。三次式が出たときは、使うか使わないかは置いといて、常に頭に思い浮かべよう。