面積と1/6公式

こんにちは、リンス(@Lins016)です。
今回は面積と1/6公式について学習していきましょう。

1/6公式が使える問題

まず確認しておきたいのが、いつでも$\small{ \ \displaystyle\frac{1}{6} \ }$公式が使えるわけじゃないってこと。

$\small{ \ \displaystyle\frac{1}{6} \ }$公式が使える面積をしっかりとマスターして、$\small{ \ \displaystyle\frac{1}{6} \ }$公式が使える問題では必ず$\small{ \ \displaystyle\frac{1}{6} \ }$公式を使うようにしよう。

1/6公式の証明

$\small{ \ \displaystyle\frac{1}{6} \ }$公式っていうのは
$\small{ \ \displaystyle\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx=-\displaystyle\frac{1}{6}(\beta-\alpha)^3 \ }$
のことだよね。

まずはこの式が成り立つことについて証明してみよう。
$\small{ \ \displaystyle\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx\\ =\displaystyle\int_{\alpha}^{\beta}(x-\alpha)(x-\alpha+\alpha-\beta)dx\\ =\displaystyle\int_{\alpha}^{\beta}\left\{(x-\alpha)^2+(\alpha-\beta)(x-\alpha)\right\}dx\\ =\left[\displaystyle\frac{1}{3}(x-\alpha)^3+\displaystyle\frac{1}{2}(\alpha-\beta)(x-\alpha)\right]_{\alpha}^{\beta}\\ =\displaystyle\frac{1}{3}(\beta-\alpha)^3+\displaystyle\frac{1}{2}(\alpha-\beta)(\beta-\alpha)^2\\ =-\displaystyle\frac{1}{6}(\beta-\alpha)^3 \ }$

つまり$\small{ \ \displaystyle\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx=-\displaystyle\frac{1}{6}(\beta-\alpha)^3 \ }$が言えるよね。

ここでは計算に

$\small{ \ \displaystyle\int(ax+b)^n dx=\displaystyle\frac{1}{a(n+1)}(ax+b)^{n+1}+C \ }$

を利用して計算を簡単にしているからね。$\small{ \ \displaystyle\int(ax+b)^n dx \ }$の形になることも多いから、この式も覚えておこう。

ただ

$\small{ \ \displaystyle\int(ax^2+b)^n dx=\displaystyle\frac{1}{a(n+1)}(ax^2+b)^{n+1}+C \ }$

とはならないから、注意しよう。あくまで括弧の中の式が一次式の時だけ利用できるんだ。

1/6公式の使い方

まず$\small{ \ \displaystyle\frac{1}{6} \ }$公式が使える面積を覚えよう。
それは
「放物線二本で囲まれた面積」
または
「放物線と直線の二本で囲まれた面積」
ってことになる。

つまり放物線を含む二次以下の関数の二本で囲まれた面積を求めるときに$\small{ \ \displaystyle\frac{1}{6} \ }$公式は利用することができるんだ。

なぜそうなるのかを考えてみよう。
$\small{ \ y=2x^2 \ }$と$\small{ \ y=2x+4 \ }$で囲まれた面積を考えてみよう。

まずは二つの線の交点を求めて
$\small{ \ 2x^2=2x+4 \ }$
$\small{ \ 2x^2-2x-4=0 \ }$
$\small{ \ 2(x-2)(x+1)=0 \ }$
$\small{ \ x=-1, \ 2 \ }$

だから求める面積は
$\small{ \ \displaystyle\int_{-1}^{2}(2x+4-2x^2)dx\\ =-\displaystyle\int_{-1}^{2}(2x^2-2x-4)dx\\ =-\displaystyle\int_{-1}^{2}2(x+1)(x-2)\\ =-2\displaystyle\int_{-1}^{2}(x+1)(x-2)dx\\ =\displaystyle\frac{2}{6}\left\{2-(-1)\right\}^3\\[15pt] =9 \ }$

これが放物線と直線で囲まれた面積の解き方になるんだ。

これを一般化した$\small{ \ y=f(x) \ }$と$\small{ \ y=g(x) \ }$で囲まれた面積を考えてみよう。

まずは二つの線の交点を求めると
$\small{ \ f(x)=g(x) \ }$
$\small{ \ f(x)-g(x)=0 \ }$
$\small{ \ a(x-\alpha)(x-\beta)=0 \ }$
$\small{ \ x=\alpha, \ \beta \ }$

求める面積は
$\small{ \ \displaystyle\int_{\alpha}^{\beta}\left\{g(x)-f(x)\right\}dx\\ =-\displaystyle\int_{\alpha}^{\beta}\left\{f(x)-g(x)\right\}dx\cdots①\\ =-\displaystyle\int_{\alpha}^{\beta}a(x-\alpha)(x-\beta)dx\cdots②\\ =-a\displaystyle\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx\\ =\displaystyle\frac{a}{6}(\beta-\alpha)^3 \ }$

つまり積分区間を求めるための$\small{ \ f(x)=g(x) \ }$を変形した$\small{ \ f(x)-g(x)=0 \ }$の左辺を$\small{ \ ① \ }$から$\small{ \ ② \ }$に変形できるから$\small{ \ \displaystyle\frac{1}{6} \ }$公式が使えるよね。

問題解答

次の二つの関数で囲まれた面積を求めよ。
(1)$\small{ \ y=2x-1, \ y=x^2-3x+5 \ }$
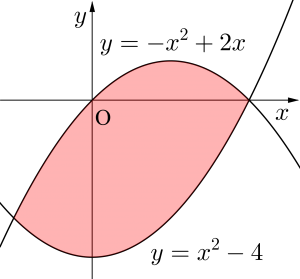
(2)$\small{ \ y=x^2-4, \ y=-x^2+2x \ }$
(3)$\small{ \ y=x^2+x, \ y=1-x \ }$

(1)
$\small{ \ x^2-3x+5=2x-1 \ }$
$\small{ \ x^2-5x+6=0 \ }$
$\small{ \ (x-2)(x-3)=0 \ }$
$\small{ \ x=2, \ 3 \ }$
$\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\int_{2}^{3}\left\{(2x-1)-(x^2-3x+5)\right\}dx\\ &=&-\displaystyle\int_{2}^{3}(x-2)(x-3)dx\\ &=&\displaystyle\frac{1}{6}(3-2)^3\\ &=&\displaystyle\frac{1}{6} \ \end{eqnarray}}$

(2)
$\small{ \ x^2-4=-x^2+2x \ }$
$\small{ \ 2x^2-2x-4=0 \ }$
$\small{ \ (x+1)(x-2)=0 \ }$
$\small{ \ x=-1, \ 2 \ }$
$\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\int_{-1}^{2}\left\{(-x^2+2x)-(x^2-4)\right\}dx\\ &=&-\displaystyle\int_{2}^{3}2(x+1)(x-2)dx\\ &=&\displaystyle\frac{2}{6}\left\{2-(-1)\right\}^3\\[15pt] &=&9 \ \end{eqnarray}}$

(3)
$\small{ \ x^2+x=1-x \ }$
$\small{ \ x^2+2x-1=0 \ }$
$\small{ \ x=-1\pm\sqrt{2} \ }$
$\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\int_{-1-\sqrt{2}}^{-1+\sqrt{2}}\left\{(1-x)-(x^2+x)\right\}dx\\ &=&-\displaystyle\int_{-1-\sqrt{2}}^{-1+\sqrt{2}}(x+1+\sqrt{2})(x+1-\sqrt{2})dx\\ &=&\displaystyle\frac{1}{6}\left\{-1+\sqrt{2}-(-1-\sqrt{2})\right\}^3\\ &=&\displaystyle\frac{8\sqrt{2}}{3} \ \end{eqnarray}}$

$\small{ \ \displaystyle\frac{1}{6} \ }$公式を利用しなくても答えは出せるけど、無理数を含む場合計算が大変だから公式を利用するようにしよう。

1/6公式が使えるの図形の面積

それじゃ今度はどんな図形の面積だったら$\small{ \ \displaystyle\frac{1}{6} \ }$公式が使えるのか確認していこう。

二次関数以下の関数二本で囲まれた面積になるからね。

放物線と直線の二本○

放物線と直線二本の計三本×

放物線と放物線の二本○

放物線二本と直線二本の計四本×

放物線と直線の二本の計三本×

放物線と直線の二本○

色々な形の面積があるけど、どの形なら$\small{ \ \displaystyle\frac{1}{6} \ }$公式が使えるかしっかりマスターしよう。
$\small{ \ \displaystyle\frac{1}{6} \ }$公式が使えるところは常に使っていくようにしよう。

Point　面積と1/6公式

①放物線と直線二本で囲まれた面積は$\small{ \ \displaystyle\frac{1}{6} \ }$公式
②放物線と放物線二本で囲まれた面積は$\small{ \ \displaystyle\frac{1}{6} \ }$公式

問題解答

$\small{ \ y=x^2-x \ }$と$\small{ \ x \ }$軸で囲まれた面積を$\small{ \ y=ax \ }$が二等分するような$\small{ \ a \ }$の値を求めよ。

$\small{ \ y=x^2-x \ }$と$\small{ \ x \ }$軸の共有点は
$\small{ \ x^2-x=0 \ }$
$\small{ \ x(x-1)=0 \ }$
$\small{ \ x=0, \ 1 \ }$
$\small{ \ y=x^2-x \ }$と$\small{ \ x \ }$軸で囲まれた面積は
$\small{ \ \displaystyle\int_{0}^{1}-(x^2-x)dx\\ =\displaystyle\frac{1}{6}(1-0)^3=\displaystyle\frac{1}{6} \ }$

$\small{ \ y=x^2-x \ }$と$\small{ \ y=ax \ }$の共有点は
$\small{ \ x^2-x=ax \ }$
$\small{ \ x(x-a-1)=0 \ }$
$\small{ \ x=0, \ a+1 \ }$
$\small{ \ y=x^2-x \ }$と$\small{ \ y=ax \ }$で囲まれた面積は
$\small{ \ \displaystyle\int_{0}^{a+1}-\left\{x^2-(a+1)x\right\}dx\\ =\displaystyle\frac{1}{6}(a+1-0)^3=\displaystyle\frac{1}{6}(a+1)^3 \ }$

よって
$\small{ \ \displaystyle\frac{1}{6}(a+1)^3=\displaystyle\frac{1}{12} \ }$
$\small{ \ (a+1)^3=\displaystyle\frac{1}{2} \ }$
$\small{ \ a+1=\displaystyle\frac{1}{\sqrt[ 3 ]{ 2 }} \ }$
$\small{ \ \therefore a=-1+\displaystyle\frac{1}{\sqrt[ 3 ]{ 2 }} \ }$

この例題みたいに$\small{ \ \displaystyle\frac{1}{6} \ }$公式を利用しないと答えを出すことができない問題も多いから$\small{ \ \displaystyle\frac{1}{6} \ }$公式が使える問題では必ず使うようにしよう。それに$\small{ \ \displaystyle\frac{1}{6} \ }$公式を使うことで計算も少なくなるから、時短にもなるし、ミスも減るし言うことなしだよね。