こんにちは、リンス(@Lins016)です。
今回は二つの文字を含む定積分で表された関数について学習していこう。
二つの文字を含む定積分
定積分に\(\small{ \ x \ }\)と\(\small{ \ t \ }\)などの二つの文字が含まれている場合、一つの文字で積分して、その文字に積分区間の上端と下端を代入するから、積分した文字は消えて、積分に関係ない文字が残ることになるんだ。
今回はこの二つの文字を含む定積分の様々なパターンについて勉強していこう。
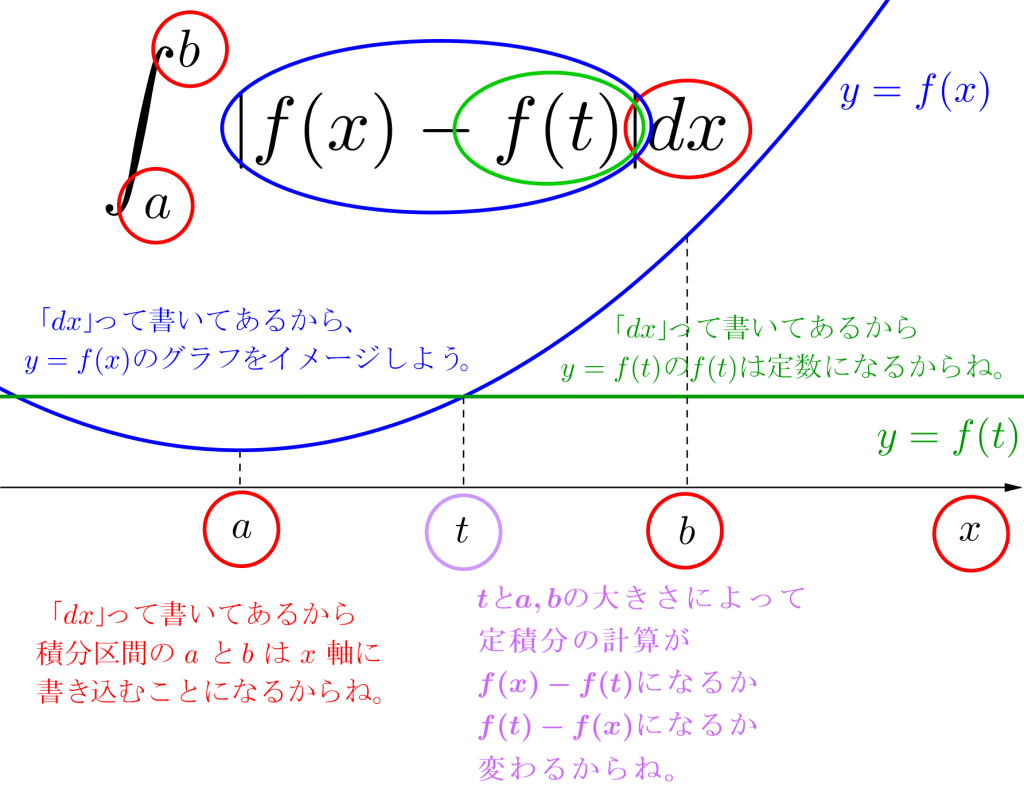
\(\small{ \ \displaystyle \int_{a}^{b}|f(x)-f(t)| dx\\
=\displaystyle \int_{a}^{t}\left\{-f(x)+f(t)\right\}dx\\
\ \ \ +\displaystyle \int_{t}^{b}\left\{f(x)-f(t)\right\}dx \ }\)
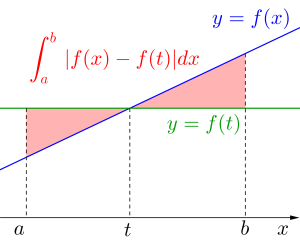
二つの文字を含む定積分
\(\small{ \ \displaystyle \int_{0}^{1} (2x-a+3) dx \ }\)や\(\small{ \ \displaystyle \int_{1}^{2} |x-t| dt \ }\)のように\(\small{ \ x \ }\)と\(\small{ \ a \ }\)や\(\small{ \ x \ }\)と\(\small{ \ t \ }\)など二つの文字が定積分に含まれている場合、\(\small{ \ \displaystyle \int_{0}^{1} (2x-a+3) dx \ }\)の定積分の最後の\(\small{ \ dx \ }\)の部分に注目しよう。
\(\small{ \ dx \ }\)って書いてある場合は\(\small{ \ x \ }\)で積分することになるから、
\(\small{\begin{eqnarray} \ &&\displaystyle \int_{0}^{1} (2x-a+3) dx\\
&&=\left[x^2-ax+3x\right]_{0}^{1}\\
&&=-a+4 \ \end{eqnarray}}\)
になるよね。
だから\(\small{ \ dx \ }\)って書いてあるときは\(\small{ \ x \ }\)で積分して\(\small{ \ x \ }\)に積分区間を代入するから、計算した値は\(\small{ \ x \ }\)が消えることになるよね。
ってことはその定積分は\(\small{ \ x \ }\)じゃないもう一つの文字の関数ってことになるからね。
\(\small{ \ a \ }\)を実数とするとき、\(\small{ \ \displaystyle \int_{0}^{1} (x^2+ax+a^2) dx \ }\)の最小値を求めよ。
\(\small{ \ \displaystyle \int_{0}^{1} (x^2+ax+a^2) dx\\
=\left[\displaystyle\frac{1}{3}x^3+\displaystyle\frac{1}{2}ax^2+a^2x\right]_{0}^{1}\\
=a^2+\displaystyle\frac{1}{2}a+\displaystyle\frac{1}{3}\\
=\left(a+\displaystyle\frac{1}{4}\right)^2+\displaystyle\frac{13}{48} \ }\)
よって\(\small{ \ a=-\displaystyle\frac{1}{4} \ }\)のとき最小値\(\small{ \ \displaystyle\frac{13}{48} \ }\)

絶対値と二つの変数を含む定積分で表された関数
次は二つの変数を含む定積分に絶対値が含まれている\(\small{ \ \displaystyle \int_{0}^{1} |x-t| dx \ }\)のような問題について考えていこう。
\(\small{ \ \displaystyle \int_{0}^{1} |x-t| dx \ }\)の場合、まず考えたくなるのが
\(\small{ \ \begin{eqnarray}
| x-t |
=
\begin{cases}
x-t & ( x \geqq t ) \\
-x+t & ( x \lt t )
\end{cases}
\end{eqnarray} \ }\)
っていう絶対値の場合分けだよね。
絶対値がある場合は、場合分けして絶対値を外したいもんね。
でもその前に考えてほしいのはどの文字で積分するのかってこと。
\(\small{ \ \displaystyle \int_{0}^{1} |x-t| dx \ }\)は\(\small{ \ dx \ }\)ってかいてあるから、\(\small{ \ x \ }\)で積分するよね。
さらに絶対値を含む定積分は絶対値の場合分けに合わせて積分区間を分割しないといけなかったよね。
忘れてる人はまず確認してから次に進もう。
ってことは絶対値を外す場合分けの範囲と積分区間\(\small{ \ 0\leqq x \leqq 1 \ }\)の関係が重要なんだ。
そもそも\(\small{ \ dx \ }\)って書いてあるから積分区間は\(\small{ \ 0\leqq x \leqq 1 \ }\)にって、\(\small{ \ y=|x-t| \ }\)は\(\small{ \ x \ }\)の式として考えるからね。
これが\(\small{ \ dt \ }\)って書いてあったら積分区間は\(\small{ \ 0\leqq t \leqq 1 \ }\)になるし、\(\small{ \ y=|x-t| \ }\)は\(\small{ \ t \ }\)の式として考えるから、場合分けも
\(\small{ \ \begin{eqnarray}
| x-t |
=
\begin{cases}
-t+x & ( t \leqq x ) \\
t-x & ( t \gt x )
\end{cases}
\end{eqnarray} \ }\)
になるからね。
だからまずは絶対値を外す場合分けの前にどの文字で積分するのか考える必要があるんだ。
次に\(\small{ \ 0\leqq x \leqq 1 \ }\)に\(\small{ \ y=|x-t| \ }\)のグラフを書き込んで考えると
\(\small{ \ t\lt 0 \ }\)のとき図のようになるから
\(\small{ \ \displaystyle \int_{0}^{1} |x-t| dx\\
=\displaystyle \int_{0}^{1}(x-t) dx\\
=\left[\displaystyle\frac{1}{2}x^2-tx\right]_{0}^{1}\\
=-t+\displaystyle\frac{1}{2} \ }\)

\(\small{ \ 0 \leqq t \lt 1 \ }\)のとき
\(\small{ \ \displaystyle \int_{0}^{1} |x-t| dx\\
=\displaystyle \int_{0}^{t}(-x+t) dx+\displaystyle \int_{t}^{1}(x-t) dx\\
=\left[-\displaystyle\frac{1}{2}x^2+tx\right]_{0}^{t}+\left[\displaystyle\frac{1}{2}x^2-tx\right]_{t}^{1}\\
=t^2-t+\displaystyle\frac{1}{2} \ }\)

\(\small{ \ t \geqq 1 \ }\)のとき
\(\small{ \ \displaystyle \int_{0}^{1} |x-t| dx\\
=\displaystyle \int_{0}^{1}(-x+t) dx\\
=\left[-\displaystyle\frac{1}{2}x^2+tx\right]_{0}^{1}\\
=t-\displaystyle\frac{1}{2} \ }\)

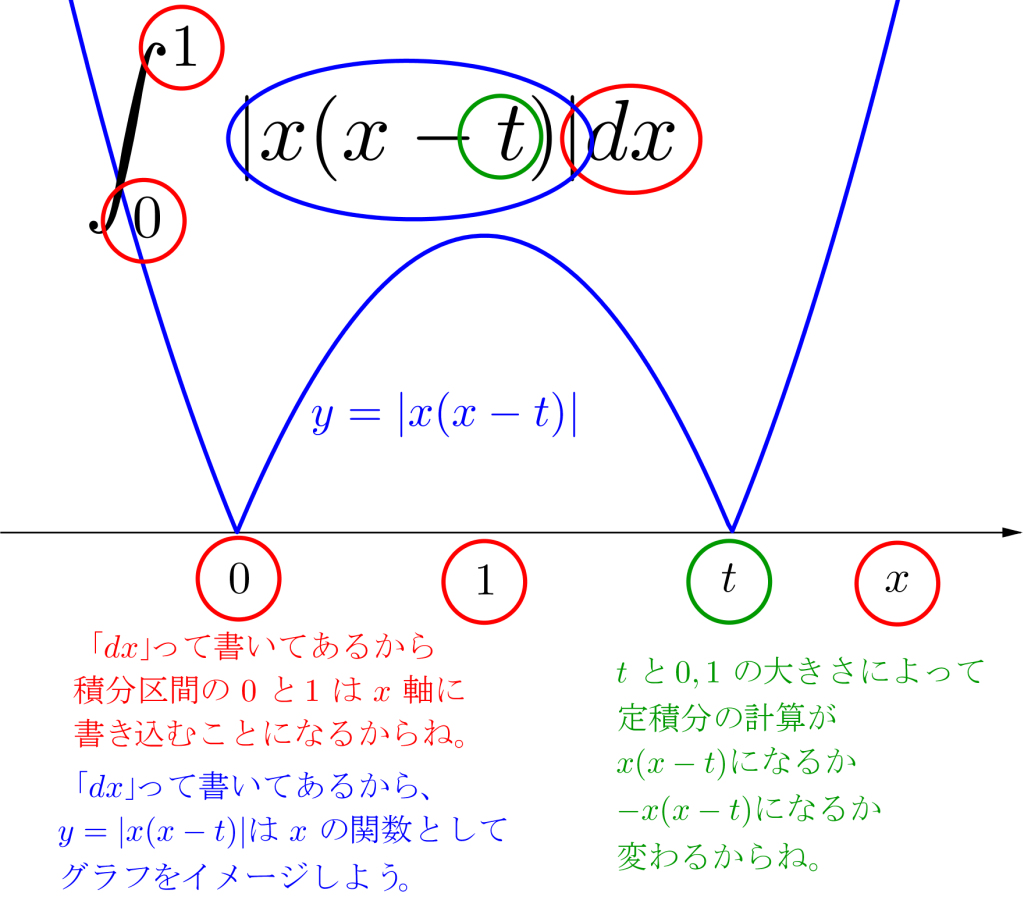
つまり\(\small{ \ \displaystyle \int_{0}^{1} |x-t| dx \ }\)を面積で考えると、\(\small{ \ x \ }\)で積分するから\(\small{ \ x \ }\)軸と積分区間の\(\small{ \ 0\leqq x \leqq 1 \ }\)を書いて、そこに\(\small{ \ y=|x-t| \ }\)を書き込もう。
そのときに\(\small{ \ t \ }\)と積分区間の位置についての場合分けが必要になるよね。
\(\small{ \ f(x)=\displaystyle \int_{0}^{1}|t(x-t)| dt \ }\)を\(\small{ \ x \ }\)の式で表し、\(\small{ \ f(x) \ }\)の最小値を求めよ。
(i)\(\small{ \ x\leqq0 \ }\)のとき
\(\small{ \ 0\leqq t \leqq1 \ }\)で\(\small{ \ \ t(x-t)\leqq 0 \ }\)
\(\small{ \ f(x)=\displaystyle \int_{0}^{1}|t(x-t)| dt\\
=\displaystyle \int_{0}^{1} t(t-x) dt\\
=\left[\displaystyle\frac{1}{3}t^3-\displaystyle\frac{1}{2}xt^2\right]_{0}^{1}\\
=-\displaystyle\frac{1}{2}x+\displaystyle\frac{1}{3} \ }\)
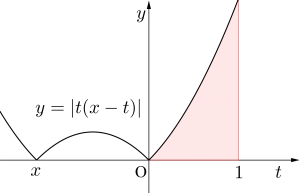
(ii)\(\small{ \ 0\lt x \lt1 \ }\)のとき
\(\small{ \ 0\leqq t \leqq x \ }\)で\(\small{ \ \ t(x-t)\geqq 0 \ }\)
\(\small{ \ x\leqq t \leqq 1 \ }\)で\(\small{ \ \ t(x-t)\leqq 0 \ }\)
\(\small{ \ f(x)=\displaystyle \int_{0}^{1}|t(x-t)| dt\\
=\displaystyle \int_{0}^{x} t(x-t) dt+\displaystyle \int_{x}^{1} t(t-x) dt\\
=\left[\displaystyle\frac{1}{2}xt^2-\displaystyle\frac{1}{3}t^3 \right]_{0}^{x}+\left[\displaystyle\frac{1}{3}t^3-\displaystyle\frac{1}{2}xt^2\right]_{x}^{1}\\
=\displaystyle\frac{1}{3}x^3-\displaystyle\frac{1}{2}x+\displaystyle\frac{1}{3} \ }\)
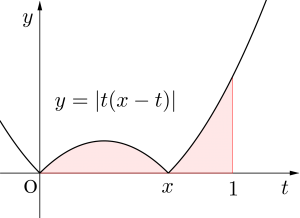
(iii)\(\small{ \ x\geqq1 \ }\)のとき
\(\small{ \ 0\leqq t \leqq1 \ }\)で\(\small{ \ \ t(x-t)\geqq 0 \ }\)
\(\small{ \ f(x)=\displaystyle \int_{0}^{1}|t(x-t)| dt\\
=\displaystyle \int_{0}^{1} t(x-t) dt\\
=\left[-\displaystyle\frac{1}{3}t^3+\displaystyle\frac{1}{2}xt^2\right]_{0}^{1}\\
=\displaystyle\frac{1}{2}x-\displaystyle\frac{1}{3} \ }\)

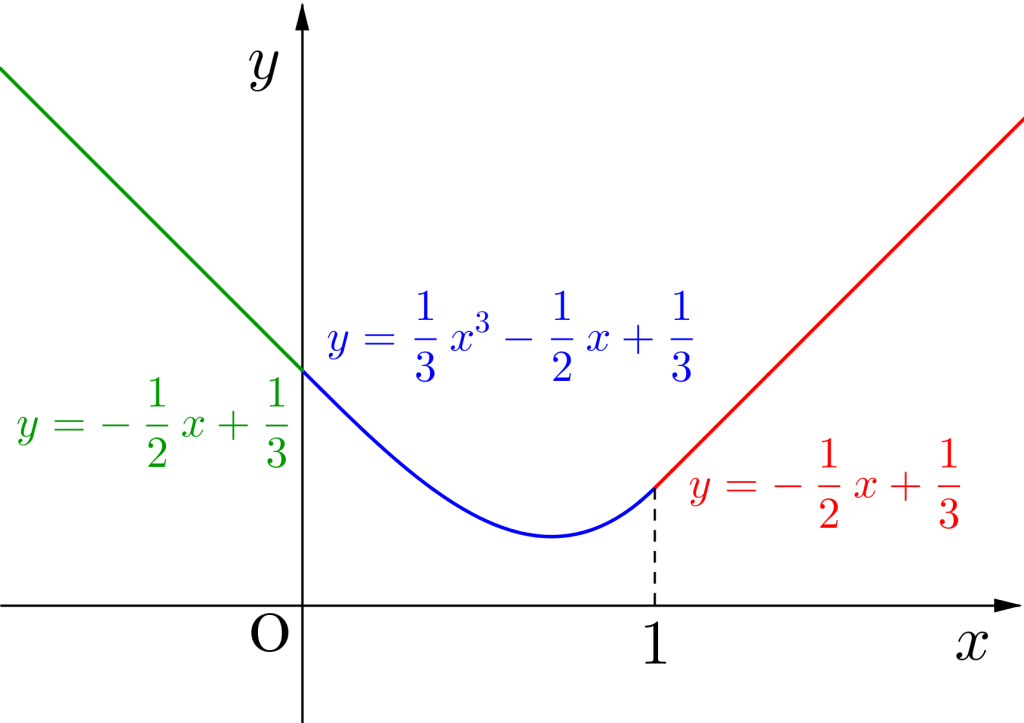
\(\small{ \ \begin{eqnarray}
f(x)
=
\begin{cases}
-\displaystyle\frac{1}{2}x+\displaystyle\frac{1}{3} & ( x \leqq 0 ) \\
\displaystyle\frac{1}{3}x^3-\displaystyle\frac{1}{2}x+\displaystyle\frac{1}{3}&( 0 \lt x\lt 1 )\\
\displaystyle\frac{1}{2}x-\displaystyle\frac{1}{3} & ( x \geqq 1 )
\end{cases}
\end{eqnarray} \ }\)
\(\small{ \ 0 \lt x \lt 1 \ }\)のとき
\(\small{ \ f(x)=\displaystyle\frac{1}{3}x^3-\displaystyle\frac{1}{2}x+\displaystyle\frac{1}{3} \ }\)
\(\small{ \ f'(x)=x^2-\displaystyle\frac{1}{2} \ }\)
\(\small{ \ f'(x)=0 \ }\)とすると\(\small{ \ x=\pm\displaystyle\frac{1}{\sqrt{2}} \ }\)
\(\small{ \ \begin{array}{c|ccccc}
t & 0& \cdots & \displaystyle \frac{1}{\sqrt{2}} & \cdots & 1 \\
\hline
g’(t) & & - & 0 & + & \\
\hline
g(t) & \displaystyle\frac{1}{3} & \searrow & \displaystyle\frac{2-\sqrt{2}}{6} & \nearrow & \displaystyle\frac{1}{6}
\end{array} \ }\)
よって最小値は
\(\small{ \ x=\displaystyle\frac{1}{\sqrt{2}} \ }\)のとき\(\small{ \ \displaystyle\frac{2-\sqrt{2}}{6} \ }\)

Point 二つの文字を含んだ定積分で表された関数
①積分する文字に注目する
②積分する文字を軸とする図形をイメージして面積を考える
③絶対値の場合分けと積分区間の場合分けを合わせて考える

