こんにちは、リンス(@Lins016)です。
今回は絶対値を含む定積分の計算について学習していきましょう。
定積分と絶対値
絶対値を含む関数は、絶対値の中が\(\small{ \ 0 \ }\)以上か\(\small{ \ 0 \ }\)未満かに場合分けをして関数を分けることから始めよう。
その上で絶対値の場合分けの範囲によっては積分区間も分割することになるからね。
\(\small{ \ \begin{eqnarray}
| f(x) |
=
\begin{cases}
f(x) & ( x \geqq \alpha ) \\
-f(x) & ( x \lt \alpha )
\end{cases}
\end{eqnarray} \ }\)

\(\small{ \ a \lt \alpha \lt b \ }\)のとき
絶対値記号の外し方
絶対値を含む関数は、必ず絶対値記号を外そう。
ただ、絶対値記号を外すとき「絶対値記号をそのまま外す場合」と「マイナスをつけて絶対値記号を外す場合」があるから、\(\small{ \ x \ }\)の範囲に注意して絶対値記号を外そう。
絶対値記号の外し方が怪しい人はもう一度チェックしておこう。
絶対値記号を含む定積分の計算
それじゃ次の三つの絶対値記号を含むの定積分について考えてみよう。
①\(\small{ \ \displaystyle\int_{0}^{2}|x-3|dx \ }\)
②\(\small{ \ \displaystyle\int_{2}^{4}|x-3|dx \ }\)
③\(\small{ \ \displaystyle\int_{4}^{6}|x-3|dx \ }\)
被積分関数はどの定積分も\(\small{ \ |x-3| \ }\)だよね。
これは
\(\small{ \ x\lt3 \ }\)なら\(\small{ \ -(x-3) \ }\)
\(\small{ \ x\geqq3 \ }\)なら\(\small{ \ x-3 \ }\)
になる関数だよね。
これに対して①~③は積分区間が異なるから、それぞれの定積分は次のようになるからね。
①\(\small{ \ \displaystyle\int_{0}^{2}|x-3|dx \ }\)の積分区間は
\(\small{ \ 0\leqq x \leqq 2 \ }\)だから、
その区間では
\(\small{ \ |x-3|=-(x-3) \ }\)になるよね。
だから
\(\small{ \ \displaystyle\int_{0}^{2}|x-3|dx=\displaystyle\int_{0}^{2}-(x-3)dx \ }\)
になるんだ。

②\(\small{ \ \displaystyle\int_{2}^{4}|x-3|dx \ }\)の積分区間は
\(\small{ \ 2\leqq x \leqq 4 \ }\)だから、
\(\small{ \ 2\leqq x \lt3 \ }\)の区間では
\(\small{ \ |x-3|=-(x-3) \ }\)になるし、
\(\small{ \ 3\leqq x \leqq4 \ }\)の区間では
\(\small{ \ |x-3|=x-3 \ }\)に
なるからね。
だから
\(\small{\begin{eqnarray} \ &&\displaystyle\int_{2}^{4}|x-3|dx\\
&&=\displaystyle\int_{2}^{3}-(x-3)dx+\displaystyle\int_{3}^{4}(x-3)dx \ \end{eqnarray}}\)
になるんだ。

③\(\small{ \ \displaystyle\int_{4}^{6}|x-3|dx \ }\)の積分区間は
\(\small{ \ 4\leqq x \leqq 6 \ }\)だから、
その区間では
\(\small{ \ |x-3|=x-3 \ }\)になるよね。
だから
\(\small{ \ \displaystyle\int_{4}^{6}|x-3|dx=\displaystyle\int_{4}^{6}(x-3)dx \ }\)
になるんだ。

絶対値で関数が囲まれているとその関数は負にならないから、求める定積分は面積でもあるからね。
次の定積分の値を求めよ。
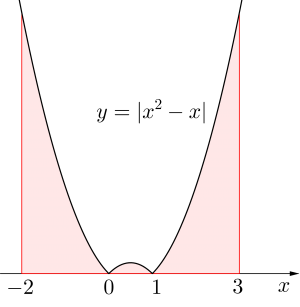
\(\small{ \ \displaystyle\int_{-2}^{3}|x^2-x|dx \ }\)
=\displaystyle\int_{-2}^{0}(x^2-x)dx+\displaystyle\int_{0}^{1}-(x^2-x)dx+\displaystyle\int_{1}^{3}(x^2-x)dx\\
=\left[\displaystyle\frac{1}{3}x^3-\displaystyle\frac{1}{2}x^2 \right]_{-2}^{0}+\left[-\displaystyle\frac{1}{3}x^3+\displaystyle\frac{1}{2}x^2 \right]_{0}^{1}+\left[\displaystyle\frac{1}{3}x^3-\displaystyle\frac{1}{2}x^2 \right]_{1}^{3}\\
=\displaystyle\frac{19}{2} \ }\)
関数が変化する定積分
絶対値記号を外すと\(\small{ \ |f(x)| \ }\)が\(\small{ \ f(x) \ }\)や\(\small{ \ -f(x) \ }\)になったけど、絶対値記号がなくても関数が変わる問題もあるんだ。
それは
\(\small{ \ \begin{eqnarray}
| f(x) |
=
\begin{cases}
x+2 & ( x \geqq 1 ) \\
-x+4 & ( x \lt 1 )
\end{cases}
\end{eqnarray} \ }\)
みたいな関数のこと。
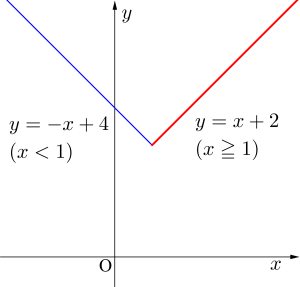
\(\small{ \ x \ }\)の範囲によって関数が変化するから、この関数を積分する場合も積分区間に注意して積分しよう。
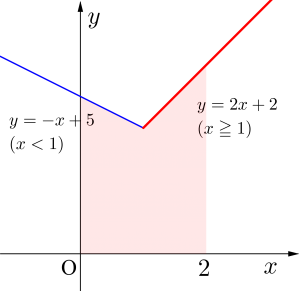
次の定積分の値を求めよ。
\(\small{ \ \begin{eqnarray}
| f(x) |
=
\begin{cases}
2x+2 & ( x \geqq 1 ) \\
-x+5 & ( x \lt 1 )
\end{cases}
\end{eqnarray} \ }\)のとき\(\small{ \ \displaystyle\int_{0}^{2}f(x)dx \ }\)
\(\small{ \ \begin{eqnarray}
| f(x) |
=
\begin{cases}
2x+2 & ( x \geqq 1 ) \\
-x+5 & ( x \lt 1 )
\end{cases}
\end{eqnarray} \ }\)より
\(\small{ \ \displaystyle\int_{0}^{2}f(x)dx\\
=\displaystyle\int_{0}^{1}(-x+5)dx+\displaystyle\int_{1}^{2}(2x+2)dx\\
=\left[-\displaystyle\frac{1}{2}x^2+5x \right]_{0}^{1}+\left[x^2+2x \right]_{1}^{2}\\
=\displaystyle\frac{19}{2} \ }\)

Point 絶対値を含む定積分の計算
①絶対値記号を場合分けして外す
②絶対値記号の場合分けの範囲と積分区間に注意して被積分関数を定める

