こんにちは、リンス(@Lins016)です。
今回は平面ベクトルの点の存在範囲について学習していきましょう。
平面ベクトルの点(終点)の存在範囲
平面ベクトルは二つの基準のベクトル\(\small{ \ \overrightarrow{\mathrm{OA}}, \ \overrightarrow{\mathrm{OB}} \ }\)を用いて\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)って表すことができたよね。
今回はこの\(\small{ \ s, \ t \ }\)に制約条件があるとき点\(\small{ \ \mathrm{P} \ }\)がどこにあるのか、点\(\small{ \ \mathrm{P} \ }\)の存在範囲を考えてみよう。
\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)
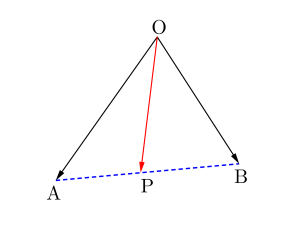
・\(\small{ \ s+t=1, s\geqq0, \ t\geqq 0 \ }\)のとき
点\(\small{ \ \mathrm{P} \ }\)は線分\(\small{ \ \mathrm{AB} \ }\)上にある
・\(\small{ \ s+t=1 \ }\)のとき
点\(\small{ \ \mathrm{P} \ }\)は直線\(\small{ \ \mathrm{AB} \ }\)上にある
・\(\small{ \ s+t\leqq1, \ s\geqq 0, \ t\geqq 0 \ }\)のとき
点\(\small{ \ \mathrm{P} \ }\)は\(\small{ \ \triangle\mathrm{OAB} \ }\)内(線上も含む)にある
内分・外分のベクトル
\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)のとき\(\small{ \ s+t=1, s\geqq0, \ t\geqq 0 \ }\)や\(\small{ \ s+t=1 \ }\)が条件の場合点\(\small{ \ \mathrm{P} \ }\)は線分\(\small{ \ \mathrm{AB} \ }\)上か直線\(\small{ \ \mathrm{AB} \ }\)上にある。
このことについては以前直線上の位置ベクトルや直線のベクトル方程式で学習したよね。
内分・外分については、下の記事を読んで復習しておこう。
内分・外分のベクトルの応用
次は\(\small{ \ 2s+3t=4 \ }\)や\(\small{ \ 2s+3t=4, s\geqq0, \ t\geqq 0 \ }\)が条件の場合\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)の存在範囲について考えてみよう。
\(\small{ \ s+t=1 \ }\)のとき点\(\small{ \ \mathrm{P} \ }\)は直線\(\small{ \ \mathrm{AB} \ }\)上にあったから、これを利用して考えてみよう。
まずは係数を足したら\(\small{ \ 1 \ }\)にしよう。
この足したら\(\small{ \ 1 \ }\)ってのが重要なんだ。
\(\small{ \ 2s+3t=4 \ }\)を両辺\(\small{ \ 4 \ }\)で割って
\(\small{ \ \displaystyle\frac{s}{2}+\displaystyle\frac{3}{4}t=1 \ }\)
これで足したら\(\small{ \ 1 \ }\)の形になったよね。
点\(\small{ \ \mathrm{P} \ }\)の位置を表すベクトルは\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)だから、この式を\(\small{ \ \displaystyle\frac{s}{2}+\displaystyle\frac{3}{4}t=1 \ }\)を利用する形に変形していくんだ。
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OP}}&=&s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}\\
&=&\displaystyle\frac{s}{2}\cdot2\overrightarrow{\mathrm{OA}}+\displaystyle\frac{3}{4}t\cdot\displaystyle\frac{4}{3}\overrightarrow{\mathrm{OB}} \ \end{eqnarray}}\)
このとき
\(\small{ \ \displaystyle\frac{s}{2}=s', \ \displaystyle\frac{3}{4}t=t' \ }\)
\(\small{ \ 2\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{OA'}}, \ \displaystyle\frac{4}{3}\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OB'}} \ }\)
とすると
\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)
\(\small{ \ \displaystyle\frac{s}{2}+\displaystyle\frac{3}{4}t=1 \ }\)は
\(\small{ \ \overrightarrow{\mathrm{OP}}=s'\overrightarrow{\mathrm{OA'}}+t'\overrightarrow{\mathrm{OB'}} \ }\)
\(\small{ \ s'+t'=1 \ }\)になる
つまり点\(\small{ \ \mathrm{P} \ }\)は直線\(\small{ \ \mathrm{A'B'} \ }\)上に存在することになるよね。
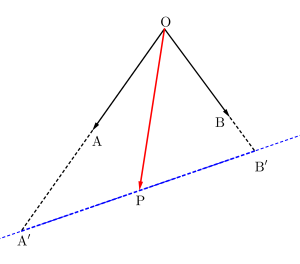
さらに\(\small{ \ s\geqq0, \ t\geqq 0 \ }\)なら\(\small{ \ s'\geqq0, \ t'\geqq 0 \ }\)になるから線分\(\small{ \ \mathrm{A'B'} \ }\)上に存在するよね。
だから常に\(\small{ \ s, \ t \ }\)の足し算(引き算)が条件になっている場合は和を\(\small{ \ 1 \ }\)にして存在範囲を考えよう。
不等式の存在範囲
次に\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)で\(\small{ \ s+t\leqq1, \ s\geqq 0, \ t\geqq 0 \ }\)のときの点\(\small{ \ \mathrm{P} \ }\)の存在範囲について考えてみよう。
今度は\(\small{ \ s+t\leqq1 \ }\)って不等式になるけど、そう難しく考える必要はないんだ。
まずは\(\small{ \ s+t=1, \ s\geqq 0, \ t\geqq 0 \ }\)のとき、点\(\small{ \ \mathrm{P} \ }\)は線分\(\small{ \ \mathrm{AB} \ }\)上だよね。
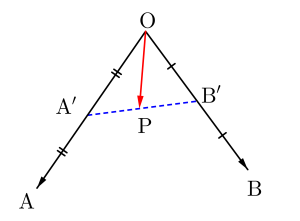
次に\(\small{ \ s+t=\displaystyle\frac{1}{2}, \ s\geqq 0, \ t\geqq 0 \ }\)のとき、
\(\small{ \ 2s+2t=1 \ }\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OP}}&=&s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}\\
&=&2s\left(\displaystyle\frac{1}{2}\overrightarrow{\mathrm{OA}}\right)+2t\left(\displaystyle\frac{1}{2}\overrightarrow{\mathrm{OB}}\right) \ \end{eqnarray}}\)
になるから
\(\small{ \ \overrightarrow{\mathrm{OA'}}=\displaystyle\frac{1}{2}\overrightarrow{\mathrm{OA}}, \ \overrightarrow{\mathrm{OB'}}=\displaystyle\frac{1}{2}\overrightarrow{\mathrm{OB}} \ }\)とすると
点\(\small{ \ \mathrm{P} \ }\)は線分\(\small{ \ \mathrm{A'B'} \ }\)上になるよね。
さらに\(\small{ \ s+t=\displaystyle\frac{1}{3}, \ s\geqq 0, \ t\geqq 0 \ }\)のとき、
\(\small{ \ 3s+3t=1 \ }\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OP}}&=&s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}\\
&=&3s\left(\displaystyle\frac{1}{3}\overrightarrow{\mathrm{OA}}\right)+3t\left(\displaystyle\frac{1}{3}\overrightarrow{\mathrm{OB}}\right) \ \end{eqnarray}}\)
になるから
\(\small{ \ \overrightarrow{\mathrm{OA''}}=\displaystyle\frac{1}{3}\overrightarrow{\mathrm{OA}}, \ \overrightarrow{\mathrm{OB''}}=\displaystyle\frac{1}{3}\overrightarrow{\mathrm{OB}} \ }\)とすると
点\(\small{ \ \mathrm{P} \ }\)は線分\(\small{ \ \mathrm{A''B''} \ }\)上になるよね。
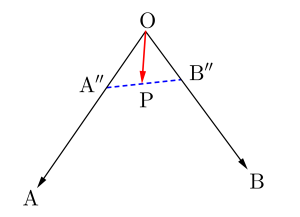
だから\(\small{ \ s+t \ }\)を\(\small{ \ 1 \ }\)から小さくしていくと線分\(\small{ \ \mathrm{AB} \ }\)に平行な線分上に点\(\small{ \ \mathrm{P} \ }\)が存在することになる。
つまり\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)で\(\small{ \ s+t\leqq1, \ s\geqq 0, \ t\geqq 0 \ }\)を満たすとき点\(\small{ \ \mathrm{P} \ }\)は\(\small{ \ \triangle\mathrm{OAB} \ }\)内(線上も含む)に存在するんだ。
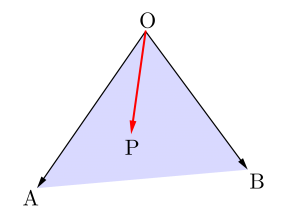
不等式の存在範囲の応用
それじゃ次は\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)で\(\small{ \ 1 \leqq 2s+3t\leqq 4, \ s\geqq 0, \ t\geqq 0 \ }\)のときの点\(\small{ \ \mathrm{P} \ }\)の存在範囲について考えてみよう。
この不等式\(\small{ \ 1 \leqq 2s+3t\leqq 4 \ }\)を一気に考えるのは難しいから\(\small{ \ 2s+3t \geqq1 \ }\)と\(\small{ \ 2s+3t\leqq 4\ }\)についてそれぞれ考えていこう。
まずは\(\small{ \ 2s+3t \geqq1 \ }\)のとき
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OP}}&=&s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}\\
&=&2s\cdot\displaystyle\frac{1}{2}\overrightarrow{\mathrm{OA}}+3t\cdot\displaystyle\frac{1}{3}\overrightarrow{\mathrm{OB}} \ \end{eqnarray}}\)
さっきと同じように
\(\small{ \ 2s=s', \ 3t=t', \ \displaystyle\frac{1}{2}\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{OA'}}, \ \displaystyle\frac{1}{3}\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OB'}} \ }\)
とすると
\(\small{ \ \overrightarrow{\mathrm{OP}}=s'\overrightarrow{\mathrm{OA'}}+t'\overrightarrow{\mathrm{OB'}} \ }\)で\(\small{ \ s'+t'\geqq 1, \ s'\geqq0, \ t'\geqq 0 \ }\)になるから図は次のようになるよね。
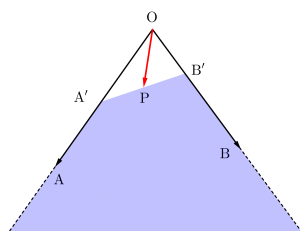
次に\(\small{ \ 2s+3t\leqq 4 \ }\)のとき
まずはこの式の両辺を\(\small{ \ 4 \ }\)で割って
\(\small{ \ \displaystyle\frac{s}{2}+\displaystyle\frac{3}{4}t \leqq 1 \ }\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OP}}&=&s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}\\
&=&\displaystyle\frac{1}{2}s\cdot2\overrightarrow{\mathrm{OA}}+\displaystyle\frac{3}{4}t\cdot\displaystyle\frac{4}{3}\overrightarrow{\mathrm{OB}} \ \end{eqnarray}}\)
\(\small{ \ \displaystyle\frac{1}{2}s=s'', \ \displaystyle\frac{3}{4}t=t'', \ 2\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{OA''}}, \ \displaystyle\frac{4}{3}\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OB''}} \ }\)
とすると
\(\small{ \ \overrightarrow{\mathrm{OP}}=s''\overrightarrow{\mathrm{OA''}}+t''\overrightarrow{\mathrm{OB''}} \ }\)で\(\small{ \ s''+t''\leqq 1, \ s''\geqq0, \ t''\geqq 0 \ }\)になるから図は次のようになるよね。
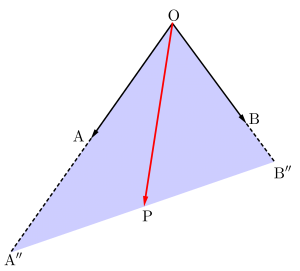
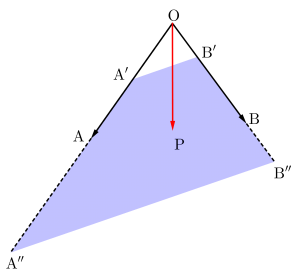
だからこの二つの図をまとめると求める存在範囲は図の範囲になるんだ。
平行四辺形の存在範囲
最後に\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)で\(\small{ \ 1\leqq s \leqq2, \ 0\leqq t \leqq 1 \ }\)のときの点\(\small{ \ \mathrm{P} \ }\)の存在範囲について考えてみよう。
\(\small{ \ 1\leqq s \leqq2, \ 0\leqq t \leqq 1 \ }\)だと\(\small{ \ 1\leqq s+t \leqq 3 \ }\)ってしたくなるけど、これは間違いだから注意しよう。
なぜかって\(\small{ \ s+t=3 \ }\)のとき\(\small{ \ s=2, \ t=1 \ }\)は条件を満たすけど、\(\small{ \ s=1, \ t=2 \ }\)だと条件を満たさないよね。
つまり\(\small{ \ 1\leqq s \leqq2, \ 0\leqq t \leqq 1 \ }\)だからといって、\(\small{ \ 1\leqq s+t \leqq 3 \ }\)になるとは言えないんだ。
だから、この場合は一つの文字を固定して考えていくんだ。\(\small{ \ s \ }\)を固定して考えてみよう。
\(\small{ \ s=1, \ 0\leqq t \leqq 1 \ }\)のとき
\(\small{ \ \overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)だから
点\(\small{ \ \mathrm{P} \ }\)は図の赤いベクトル上に存在する。

\(\small{ \ s=\displaystyle\frac{3}{2}, \ 0\leqq t \leqq 1 \ }\)のとき
\(\small{ \ \overrightarrow{\mathrm{OP}}=\displaystyle\frac{3}{2}\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)だから
点\(\small{ \ \mathrm{P} \ }\)は図の赤いベクトル上に存在する。

\(\small{ \ s=2, \ 0\leqq t \leqq 1 \ }\)のとき
\(\small{ \ \overrightarrow{\mathrm{OP}}=2\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)だから
点\(\small{ \ \mathrm{P} \ }\)は図の赤いベクトル上に存在する。

だから\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)で\(\small{ \ 1\leqq s \leqq2, \ 0\leqq t \leqq 1 \ }\)のときの点\(\small{ \ \mathrm{P} \ }\)の存在範囲は図のような平行四辺形になるからね。
\(\small{ \ s+t=1 \ }\)のような形で作られる直線にはならないから注意しよう。

ちなみにこの平行四辺形の角は
\(\small{ \ (s,t)=(1,0),(1,1),(2,0),(2,1) \ }\)のときの点\(\small{ \ \mathrm{P} \ }\)の位置だから覚えておこう。
Point 平面ベクトルの存在範囲
\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)のとき
①\(\small{ \ s+t=1 \ }\)なら直線\(\small{ \ \mathrm{AB} \ }\)上
②\(\small{ \ s+t\leqq 1, \ s\geqq0, \ t\geqq0 \ }\)なら\(\small{ \ \triangle\mathrm{OAB} \ }\)内
③和・差の条件式は\(\small{ \ s'+t'=1 \ }\)の形に変形する
\(\small{ \ \triangle\mathrm{OAB} \ }\)と点\(\small{ \ \mathrm{P} \ }\)があり、実数\(\small{ \ k, \ m, \ n \ }\)に対して\(\small{ \ k\overrightarrow{\mathrm{PO}}+m\overrightarrow{\mathrm{PA}}+n\overrightarrow{\mathrm{PB}}=\overrightarrow{0} \ }\)が成り立つ。
点\(\small{ \ \mathrm{P} \ }\)が\(\small{ \ k\geqq1, \ m\geqq0, \ n\geqq0, \ m+n=3 \ }\)を満たしながら動くとき、点\(\small{ \ \mathrm{P} \ }\)の存在範囲を図示せよ。またこの存在範囲の面積は\(\small{ \ \triangle\mathrm{OAB} \ }\)の何倍になるか。
\(\small{ \ k\overrightarrow{\mathrm{PO}}+m\overrightarrow{\mathrm{PA}}+n\overrightarrow{\mathrm{PB}}=\overrightarrow{0} \ }\)
\(\small{ \ (k+m+n)\overrightarrow{\mathrm{OP}}=m\overrightarrow{\mathrm{OA}}+n\overrightarrow{\mathrm{OB}} \ }\)
\(\small{ \ m+n=3 \ }\)より
\(\small{ \ \displaystyle\frac{m}{3}+\displaystyle\frac{n}{3}=1 \ }\)
\(\small{ \ (k+3)\overrightarrow{\mathrm{OP}}=3\left(\displaystyle\frac{m}{3}\overrightarrow{\mathrm{OA}}+\displaystyle\frac{n}{3}\overrightarrow{\mathrm{OB}}\right) \ }\)
\(\small{ \ \overrightarrow{\mathrm{OP}}=\displaystyle\frac{3}{k+3}\left(\displaystyle\frac{m}{3}\overrightarrow{\mathrm{OA}}+\displaystyle\frac{n}{3}\overrightarrow{\mathrm{OB}}\right) \ }\)
また\(\small{ \ k\geqq1 \ }\)より\(\small{ \ 0\lt \displaystyle\frac{3}{k+3}\leqq \displaystyle\frac{3}{4} \ }\)
\(\small{ \ \displaystyle\frac{m}{3}\overrightarrow{\mathrm{OA}}+\displaystyle\frac{n}{3}\overrightarrow{\mathrm{OB}} \ }\)は線分\(\small{ \ \mathrm{AB} \ }\)上を動くことになるので求める存在範囲は図のようになる。

よって面積は相似比の二乗だから
\(\small{\begin{eqnarray} \ S_{\triangle\mathrm{OA'B'}}&=&\displaystyle\frac{3}{4}\cdot\displaystyle\frac{3}{4}S_{\triangle\mathrm{OAB}}\\
&=&\displaystyle\frac{9}{16}S_{\triangle\mathrm{OAB}} \ \end{eqnarray}}\)

