直線のベクトル方程式

こんにちは、リンス(@Lins016)です。
今回は直線のベクトル方程式について学習していこう。

直線のベクトル方程式の解き方

ベクトル方程式は前回学習したように、ある条件を満たす\(\small{ \ \mathrm{P} \left(\overrightarrow{ p }\right) \ }\)の方程式のことで、点 \(\small{ \ \mathrm{P} \ }\)の集合、つまり軌跡が線になるんだ。
今回はその中でも直線のベクトル方程式について学習していこう。

まず直線は次の三つのパターンがあることを確認しよう。

それは「ある点を通り、ある直線（ベクトル）に平行な直線」「二点を通る直線」「ある点を通り、ある直線（ベクトル）に垂直な直線」で、この三つの直線のベクトル方程式を考えてみよう。

点Aを通り\(\small{ \ \overrightarrow{ d } \ }\)に平行な直線のベクトル方程式

\(\small{ \ \overrightarrow{ p }= \overrightarrow{ a }+t \overrightarrow{ d } \ }\)

これは\(\small{ \ t \ }\)の値が変化すると、点\(\small{ \ \mathrm{P}\left( \overrightarrow{ p }\right) \ }\)の点の集合は直線になるよね。

つまり点\(\small{ \ \mathrm{A}\left(\overrightarrow{ a }\right) \ }\)を通って\(\small{ \ \overrightarrow{ d } \ }\)に平行な直線になるんだ。

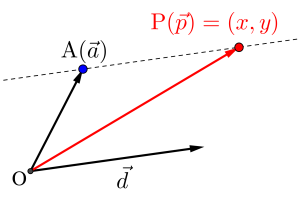
成分表示の問題では\(\small{ \ \overrightarrow{ p }= (x, \ y) \ }\)とすると媒介変数\(\small{ \ t \ }\)を使って、\(\small{ \ (x, \ y)= \left( \ f(t), \ g(t) \ \right) \ }\)のように媒介変数で位置を表すことができる。

媒介変数で表された軌跡の方程式の問題と同じで、これから媒介変数を消去して\(\small{ \ x, \ y \ }\)の関係式を作ることで、\(\small{ \ \overrightarrow{ p } \ }\)の位置を表す方程式を求めることができるんだ。

問題解答

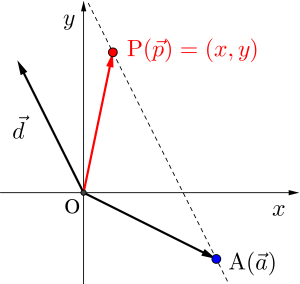
点\(\small{ \ \mathrm{A}(2, \ -1) \ }\)を通り、\(\small{ \ \overrightarrow{ d }=(-1, \ 2) \ }\)に平行な直線の媒介変数表示を媒介変数\(\small{ \ t \ }\)を用いて求めよ。また、\(\small{ \ t \ }\)を消去した直線の方程式を求めよ。

\(\small{ \ \overrightarrow{ p }=(x, \ y) \ }\)、\(\small{ \ \overrightarrow{ a }=(2, \ -1) \ }\)とすると
\(\small{ \ \overrightarrow{ p }= \overrightarrow{ a }+t \overrightarrow{ d } \ }\)
\(\small{\begin{eqnarray} \ (x, \ y)&=&(2, \ -1)+t(-1, \ 2)\\
&=&(-t+2, \ 2t-1) \ \end{eqnarray}}\)
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
x=-t+2\\
y=2t-1
\end{array}
\right.
\end{eqnarray} \ }\)
これから\(\small{ \ t \ }\)を消去して
\(\small{\begin{eqnarray} \ y&=&2(-x+2)-1\\
&=&-2x+3 \ \end{eqnarray}}\)

二点を通る直線のベクトル方程式

二点を通る直線の方程式は「直線上の位置ベクトルの表し方」で学習したように点\(\small{ \ \mathrm{A}\left(\overrightarrow{ a }\right) \ }\)と点\(\small{ \ \mathrm{B}\left(\overrightarrow{ b }\right) \ }\)を通る直線上の点\(\small{ \ \mathrm{P}\left(\overrightarrow{ p }\right) \ }\)の満たす条件式は \(\small{ \ \overrightarrow{ p }=s \overrightarrow{ a }+t \overrightarrow{ b } \ }\)とすると\(\small{ \ s+t=1 \ }\)になる。

つまり \(\small{ \ \overrightarrow{ p }=(1-t) \overrightarrow{ a }+t \overrightarrow{ b } \ }\)

これは
\(\small{\begin{eqnarray} \ \overrightarrow{ \mathrm{OP} }&=&(1-t) \overrightarrow{ \mathrm{OA} }+t \overrightarrow{ \mathrm{OB} }\\
&=& \overrightarrow{ \mathrm{OA} }+t \overrightarrow{ \mathrm{AB} } \ \end{eqnarray}}\)
とも変形できる。

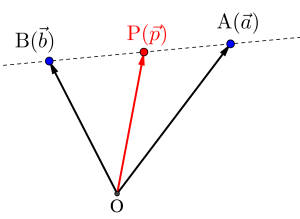
だから点\(\small{ \ \mathrm{A} \ }\)を通り\(\small{ \ \overrightarrow{ \mathrm{AB} } \ }\)に平行な直線のベクトル方程式ともいえるからね。

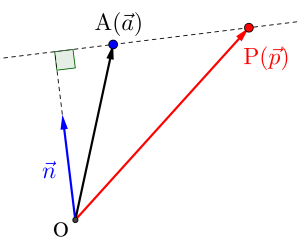
点Aを通り\(\small{ \ \overrightarrow{ n } \ }\)に垂直な直線のベクトル方程式

直線に垂直なベクトルのことを法線ベクトルっていうから覚えておこう。

法線ベクトルは垂直ならどんな大きさでもいいから、一つの直線に対する法線ベクトルは無数にあるから注意しよう。

ベクトルでは垂直って言ったら内積を利用するからね。

だから点\(\small{ \ \mathrm{A} \ }\)を通って\(\small{ \ \overrightarrow{ n } \ }\)に垂直な直線のベクトル方程式の場合も内積を利用してベクトル方程式を表そう。

\(\small{ \ \overrightarrow{ \mathrm{AP} }\cdot \overrightarrow{ n }=0 \ }\)
\(\small{ \ \left(\overrightarrow{ p }- \overrightarrow{ a }\right)\cdot \overrightarrow{ n }=0 \ }\)

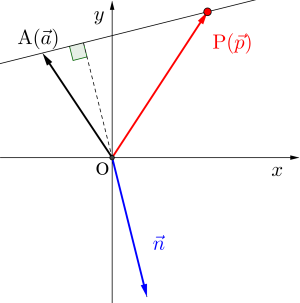
成分表示の問題の場合は、成分の内積から直線の方程式を導くことができるから例題で確認しておこう。

問題解答

点\(\small{ \ \mathrm{A}(-2, \ 3) \ }\)を通り、\(\small{ \ \overrightarrow{ n }=(1, \ -4) \ }\)が法線ベクトルである直線の方程式を求めよ。

\(\small{ \ \overrightarrow{ p }=(x, \ y) \ }\)、\(\small{ \ \overrightarrow{ a }=(-2, \ 3) \ }\)とすると、
\(\small{ \ \left(\overrightarrow{ p }- \overrightarrow{ a }\right)\cdot \overrightarrow{ n }=0 \ }\)
\(\small{ \ \left\{(x, \ y)-(-2, \ 3)\right\}\cdot (1, \ -4)=0 \ }\)
\(\small{ \ (x+2, \ y-3)\cdot(1, \ -4)=0 \ }\)
\(\small{ \ x+2-4(y-3)=0 \ }\)
\(\small{ \ \therefore x-4y+14=0 \ }\)

軌跡や領域をベクトルで表す問題もあって、その中には直線のベクトル方程式から答える問題もあるから、今回学習したところは基本的なところになるだけどしっかり押さえておこう。

Point 直線のベクトル方程式

①点\(\small{ \ \mathrm{P}\left(\overrightarrow{ p }\right) \ }\)のベクトル方程式を作ろう
②直線は三つ形のベクトル方程式をマスターしよう