こんにちは、リンス(@Lins016)です。
今回は外心・重心・垂心とオイラー線について学習していこう。
三角形の外心と重心と垂心とオイラー線
三角形の外心と重心と垂心は三角形が正三角形はじゃないとき一本の直線上にあるんだ。
この直線のことをオイラー線っていうんだ。
今回はこのオイラー線を外心を始点にしたベクトルで考えてみよう。
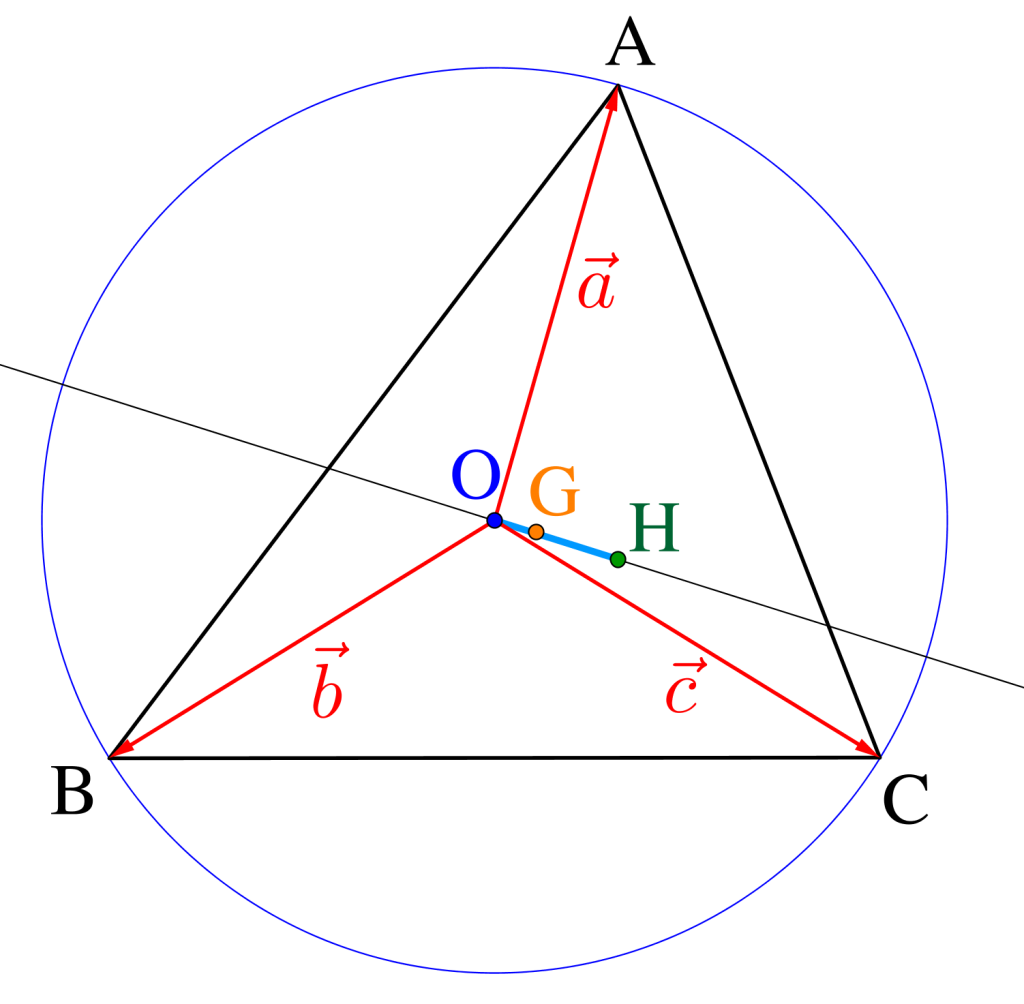
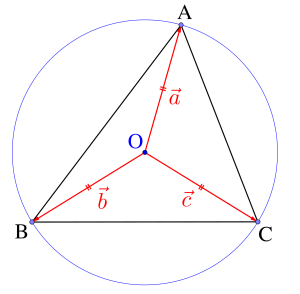
外心\(\small{ \ \mathrm{O} \ }\)を基準にした位置ベクトル
\(\small{ \ \triangle \mathrm{ABC} \ }\)についての問題は\(\small{ \ \overrightarrow{ \mathrm{AB} } \ }\)と\(\small{ \ \overrightarrow{ \mathrm{AC} } \ }\)の二つのベクトルを基準にすることがほとんどだったけど、外心\(\small{ \ \mathrm{O} \ }\)を始点に\(\small{ \ \overrightarrow{ \mathrm{OA} } \ }\)、\(\small{ \ \overrightarrow{ \mathrm{OB} } \ }\)、\(\small{ \ \overrightarrow{ \mathrm{OC} } \ }\)の三つのベクトルを利用する場合がある。
この場合\(\small{ \ \mathrm{O} \ }\)は外心だから\(\small{ \ \left| \overrightarrow{ \mathrm{OA} }\right|=\left| \overrightarrow{ \mathrm{OB} }\right|=\left| \overrightarrow{ \mathrm{OC} }\right| \ }\)になるよね。
さらに重心\(\small{ \ \mathrm{G} \ }\)は\(\small{ \ \overrightarrow{ \mathrm{OG} }= \displaystyle \frac{\overrightarrow{ \mathrm{OA} }+ \overrightarrow{ \mathrm{OB} }+ \overrightarrow{ \mathrm{OC} }}{3} \ }\)になるからね。
垂心を表す位置ベクトル
\(\small{ \ \overrightarrow{ \mathrm{OH} }= \overrightarrow{ \mathrm{OA} }+ \overrightarrow{ \mathrm{OB} }+ \overrightarrow{ \mathrm{OC} } \ }\)について考えてみよう。
\(\small{\begin{eqnarray} &&\overrightarrow{ \mathrm{AH} }\cdot \overrightarrow{ \mathrm{BC} }\\
&&=\left( \overrightarrow{ \mathrm{OH} }- \overrightarrow{ \mathrm{OA} }\right)\cdot \left( \overrightarrow{ \mathrm{OC} }- \overrightarrow{ \mathrm{OB} } \right)\\
&&=\left( \overrightarrow{ \mathrm{OB} }+ \overrightarrow{ \mathrm{OC} }\right)\cdot \left( \overrightarrow{ \mathrm{OC} }- \overrightarrow{ \mathrm{OB} } \right)\\
&&=\left| \overrightarrow{ \mathrm{OC} }\right|^2-\left| \overrightarrow{ \mathrm{OB} }\right|^2\\
&&=0 \ \end{eqnarray}}\)
\(\small{ \ \therefore \mathrm{AH}\perp \mathrm{BC} \ }\)
さらに
\(\small{\begin{eqnarray} &&\overrightarrow{ \mathrm{BH} }\cdot \overrightarrow{ \mathrm{AC} }\\
&&=\left( \overrightarrow{ \mathrm{OH} }- \overrightarrow{ \mathrm{OB} }\right)\cdot \left( \overrightarrow{ \mathrm{OC} }- \overrightarrow{ \mathrm{OA} } \right)\\
&&=\left( \overrightarrow{ \mathrm{OA} }+ \overrightarrow{ \mathrm{OC} }\right)\cdot \left( \overrightarrow{ \mathrm{OC} }- \overrightarrow{ \mathrm{OA} } \right)\\
&&=\left| \overrightarrow{ \mathrm{OC} }\right|^2-\left| \overrightarrow{ \mathrm{OA} }\right|^2\\
&&=0 \ \end{eqnarray}}\)
\(\small{ \ \therefore \mathrm{BH}\perp \mathrm{AC} \ }\)
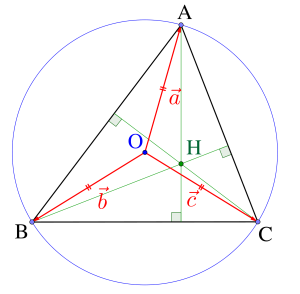
これから\(\small{ \ \mathrm{H} \ }\)は垂心ってことがわかる。
つまり外心\(\small{ \ \mathrm{O} \ }\)を始点にした三つのベクトル\(\small{ \ \overrightarrow{ \mathrm{OA} } \ }\)、\(\small{ \ \overrightarrow{ \mathrm{OB} } \ }\)、\(\small{ \ \overrightarrow{ \mathrm{OC} } \ }\)を使うとどんな\(\small{ \ \triangle \mathrm{ABC} \ }\)でも\(\small{ \ \overrightarrow{ \mathrm{OH} }= \overrightarrow{ \mathrm{OA} }+ \overrightarrow{ \mathrm{OB} }+ \overrightarrow{ \mathrm{OC} } \ }\)がいえるんだ。
オイラー線とは
\(\small{ \ \overrightarrow{ \mathrm{OG} }= \displaystyle \frac{ \overrightarrow{ \mathrm{OA} }+ \overrightarrow{ \mathrm{OB} }+ \overrightarrow{ \mathrm{OC} }}{3} \ }\)、\(\small{ \ \overrightarrow{ \mathrm{OH} }= \overrightarrow{ \mathrm{OA} }+ \overrightarrow{ \mathrm{OB} }+ \overrightarrow{ \mathrm{OC} } \ }\)になるから\(\small{ \ \overrightarrow{ \mathrm{OH} }=3 \overrightarrow{ \mathrm{OG} } \ }\)になるよね。
これは\(\small{ \ \mathrm{OH} \ }\)を\(\small{ \ 1:2 \ }\)に内分する点が\(\small{ \ \mathrm{G} \ }\)であることを示してる。
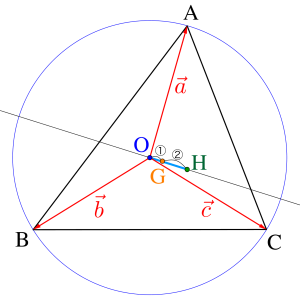
つまり外心\(\small{ \ \mathrm{O} \ }\)と重心 \(\small{ \ \mathrm{G} \ }\)と垂心\(\small{ \ \mathrm{H} \ }\)が同一直線上にあるんだ。
この直線のことをオイラー線っていってどんな三角形でも外心\(\small{ \ \mathrm{O} \ }\)と重心 \(\small{ \ \mathrm{G} \ }\)と垂心\(\small{ \ \mathrm{H} \ }\)が同一直線上にあるんだ。
ただ、正三角形は外心\(\small{ \ \mathrm{O} \ }\)と重心 \(\small{ \ \mathrm{G} \ }\)と垂心\(\small{ \ \mathrm{H} \ }\)は全て同じ点になるからこの場合だけは直線は書けないけどね。

オイラー線の問題は三角比の五心のページでも紹介しているから、ベクトルを使わない解き方も確認しておこう。
Point 外心・重心・垂心とオイラー線
①\(\small{ \ \triangle \mathrm{ABC} \ }\)の外心\(\small{ \ \mathrm{O} \ }\)、垂心\(\small{ \ \mathrm{H} \ }\)は\(\small{ \ \overrightarrow{ \mathrm{OH} }= \overrightarrow{ \mathrm{OA} }+ \overrightarrow{ \mathrm{OB} }+ \overrightarrow{ \mathrm{OC} } \ }\)の関係を満たす
②オイラー線上の外心\(\small{ \ \mathrm{O} \ }\)、重心\(\small{ \ \mathrm{G} \ }\)、垂心\(\small{ \ \mathrm{H} \ }\)は\(\small{ \ \mathrm{OG:GH}=1:2 \ }\)の関係を満たす

